SciPy in Python チュートリアル:| とは |ライブラリと関数の例
Python での SciPy
Python での SciPy 数学的、科学的、工学的、および技術的な問題を解決するために使用されるオープンソース ライブラリです。これにより、ユーザーはさまざまな高レベルの Python コマンドを使用してデータを操作し、データを視覚化できます。 SciPy は Python NumPy エクステンション上に構築されています。 SciPy は「Sigh Pi」とも発音されます。
SciPy のサブパッケージ:
- ファイルの入出力 – scipy.io
- 特殊機能 – scipy.special
- 線形代数演算 – scipy.linalg
- 補間 – scipy.interpolate
- 最適化と適合 – scipy.optimize
- 統計と乱数 – scipy.stats
- 数値積分 – scipy.integrate
- 高速フーリエ変換 – scipy.fftpack
- 信号処理 – scipy.signal
- 画像操作 – scipy.ndimage
この Python SciPy チュートリアルでは、次のことを学びます:
- SciPy とは?
- SciPy を使用する理由
- Numpy VS SciPy
- SciPy – インストールと環境設定
- ファイル入力/出力パッケージ:
- 特別機能パッケージ:
- SciPy による線形代数:
- 離散フーリエ変換 – scipy.fftpack
- SciPy の最適化と適合 – scipy.optimize
- Nelder – ミード アルゴリズム:
- SciPy による画像処理 – scipy.ndimage
SciPy を使用する理由
- SciPy には、科学計算に関連する最も一般的な問題の解決に役立つさまざまなサブパッケージが含まれています。
- Python の SciPy パッケージは、C/C++ または Matlab の GNU Scientific Library に次ぐ最も使用されている科学ライブラリです。
- 使いやすく、理解しやすく、高速な計算能力
- NumPy ライブラリの配列を操作できます。
Numpy VS SciPy ナンピー:
- Numpy は C で書かれており、数学または数値計算に使用されます。
- 他の Python ライブラリよりも高速です
- Numpy は、データ サイエンスが基本的な計算を実行するのに最も役立つライブラリです。
- Numpy には、並べ替え、整形、インデックス作成などの最も基本的な操作を実行する配列データ型しか含まれていません。
SciPy:
- SciPy は NumPy の上に構築されています
- Python の SciPy モジュールは線形代数の完全な機能を備えたバージョンですが、Numpy にはいくつかの機能しか含まれていません。
- 新しいデータ サイエンス機能のほとんどは、Numpy ではなく Scipy で利用できます。
SciPy – インストールと環境設定
pip 経由で Windows に SciPy をインストールすることもできます
Python3 -m pip install --user numpy scipy
Linux に Scipy をインストールする
sudo apt-get install python-scipy python-numpy
SciPy を Mac にインストール
sudo port install py35-scipy py35-numpy
SciPy Python の学習を開始する前に、基本的な機能と NumPy のさまざまなタイプの配列を理解する必要があります
SciPy モジュールと Numpy をインポートする標準的な方法:
from scipy import special #same for other modules import numpy as np
ファイル入力/出力パッケージ:
I/O パッケージである Scipy には、Matlab、Arff、Wave、Matrix Market、IDL、NetCDF、TXT、CSV、およびバイナリ形式のさまざまなファイル形式を操作するための幅広い機能があります。
MatLab で定期的に使用されているファイル形式の Python SciPy の例を見てみましょう:
import numpy as np
from scipy import io as sio
array = np.ones((4, 4))
sio.savemat('example.mat', {'ar': array})
data = sio.loadmat(‘example.mat', struct_as_record=True)
data['ar']
出力:
array([[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.]])
コードの説明
- 1 行目と 2 行目: I/O パッケージと Numpy を使用して、必要な SciPy ライブラリを Python にインポートします。
- 3 行目 :4 x 4 の 1 次元の配列を作成します
- 4 行目 :配列を example.mat に保存します ファイル。
- 5 行目: example.mat からデータを取得 ファイル
- 6 行目 :出力を印刷します。
特別機能パッケージ
- scipy.special パッケージには、数理物理学の多数の関数が含まれています。
- SciPy の特殊関数には、Cubic Root、Exponential、Log sum Exponential、Lambert、Permutation and Combinations、Gamma、Bessel、hypergeometric、Kelvin、beta、放物線柱、Relative Error Exponential などがあります。
- これらすべての機能を 1 行で説明するには、Python コンソールに次のように入力します。
help(scipy.special)
Output :
NAME
scipy.special
DESCRIPTION
========================================
Special functions (:mod:`scipy.special`)
========================================
.. module:: scipy.special
Nearly all of the functions below are universal functions and follow
broadcasting and automatic array-looping rules. Exceptions are noted.
立方根関数:
Cubic Root 関数は、値の立方根を見つけます。
構文:
scipy.special.cbrt(x)
例:
from scipy.special import cbrt #Find cubic root of 27 & 64 using cbrt() function cb = cbrt([27, 64]) #print value of cb print(cb)
出力: 配列([3., 4.])
指数関数:
指数関数は要素ごとに 10**x を計算します。
例:
from scipy.special import exp10 #define exp10 function and pass value in its exp = exp10([1,10]) print(exp)
出力:[1.e+01 1.e+10]
順列と組み合わせ:
SciPy は、順列と組み合わせを計算する機能も提供します。
組み合わせ – scipy.special.comb(N,k)
例:
from scipy.special import comb #find combinations of 5, 2 values using comb(N, k) com = comb(5, 2, exact = False, repetition=True) print(com)
出力:15.0
順列 –
scipy.special.perm(N,k)
例:
from scipy.special import perm #find permutation of 5, 2 using perm (N, k) function per = perm(5, 2, exact = True) print(per)
出力:20
対数合計指数関数
対数合計指数は、合計指数入力要素の対数を計算します。
構文 :
scipy.special.logsumexp(x)
ベッセル関数
N次整数次数計算機能
構文 :
scipy.special.jn()
SciPy による線形代数
- SciPy の線形代数は、BLAS および ATLAS LAPACK ライブラリの実装です。
- 線形代数のパフォーマンスは、BLAS や LAPACK に比べて非常に高速です。
- 線形代数ルーチンは 2 次元配列オブジェクトを受け入れ、出力も 2 次元配列です。
scipy.linalg を使ってテストしてみましょう。
行列式の計算 二次元行列の
from scipy import linalg import numpy as np #define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass values to det() function linalg.det( two_d_array )
出力: -7.0
逆行列 –
scipy.linalg.inv()
Scipy の逆行列は、正方行列の逆行列を計算します。
見てみましょう、
from scipy import linalg import numpy as np # define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass value to function inv() linalg.inv( two_d_array )
出力:
array( [[-0.28571429, 0.71428571],
[ 0.42857143, -0.57142857]] )
固有値と固有ベクトル
scipy.linalg.eig()
- 線形代数で最も一般的な問題は、eig() を使用して簡単に解決できる固有値と固有ベクトルです。 関数。
- 次は (X の固有値を見つけます ) と対応する 2 次元正方行列の固有ベクトル。
例
from scipy import linalg import numpy as np #define two dimensional array arr = np.array([[5,4],[6,3]]) #pass value into function eg_val, eg_vect = linalg.eig(arr) #get eigenvalues print(eg_val) #get eigenvectors print(eg_vect)
出力:
[ 9.+0.j -1.+0.j] #eigenvalues [ [ 0.70710678 -0.5547002 ] #eigenvectors [ 0.70710678 0.83205029] ]
離散フーリエ変換 – scipy.fftpack
- DFT は、空間データを周波数データに変換する際に使用される数学的手法です。
- FFT (高速フーリエ変換) は、DFT を計算するためのアルゴリズムです
- FFT は多次元配列に適用されます。
- 周波数は、特定の期間における信号または波長の数を定義します。
例: Wave を取り、Matplotlib ライブラリを使用して表示します。 sin(20 × 2πt) の単純な周期関数の例を取り上げます
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
#Frequency in terms of Hertz
fre = 5
#Sample rate
fre_samp = 50
t = np.linspace(0, 2, 2 * fre_samp, endpoint = False )
a = np.sin(fre * 2 * np.pi * t)
figure, axis = plt.subplots()
axis.plot(t, a)
axis.set_xlabel ('Time (s)')
axis.set_ylabel ('Signal amplitude')
plt.show()
出力:
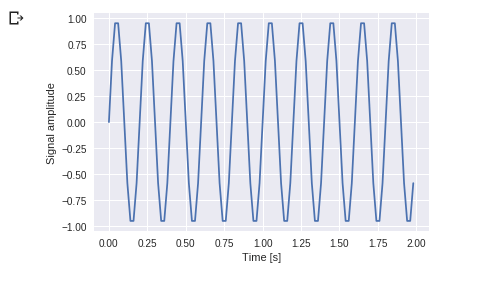
これを見ることができます。周波数は 5 Hz で、その信号は 1/5 秒で繰り返されます。これは特定の期間として呼び出されます。
それでは、DFT アプリケーションを使用してこの正弦波を使用してみましょう。
from scipy import fftpack
A = fftpack.fft(a)
frequency = fftpack.fftfreq(len(a)) * fre_samp
figure, axis = plt.subplots()
axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-fre_samp / 2, fre_samp/ 2)
axis.set_ylim(-5, 110)
plt.show()
出力:
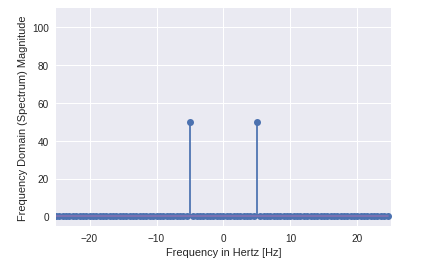
- 出力が 1 次元配列であることがはっきりとわかります。
- 複素数を含む入力は、2 つのポイントを除いてゼロです。
- DFT の例では、信号の大きさを視覚化します。
SciPy の最適化と適合 – scipy.optimize
- 最適化は、カーブ フィッティング、多次元またはスカラーおよびルート フィッティングを最小化するための便利なアルゴリズムを提供します。
- スカラー関数の例を見てみましょう 最小スカラー関数を見つける.
%matplotlib inline
import matplotlib.pyplot as plt
from scipy import optimize
import numpy as np
def function(a):
return a*2 + 20 * np.sin(a)
plt.plot(a, function(a))
plt.show()
#use BFGS algorithm for optimization
optimize.fmin_bfgs(function, 0)
出力:
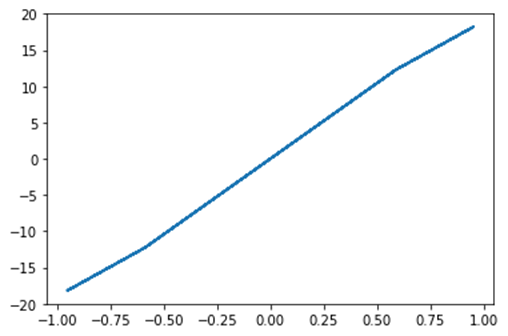
最適化は正常に終了しました。
現在の関数値:-23.241676
繰り返し:4
機能評価:18
勾配評価:6
配列([-1.67096375])
- この例では、初期点から勾配降下アルゴリズムを使用して最適化を行います
- しかし、考えられる問題は、グローバル ミニマムではなくローカル ミニマムです。大域的最小値の近傍が見つからない場合は、大域的最適化を適用し、basinhopping() として使用される大域的最小関数を見つける必要があります。 ローカル オプティマイザーを組み合わせます。
optimize.basinhopping(関数, 0)
出力:
fun: -23.241676238045315
lowest_optimization_result:
fun: -23.241676238045315
hess_inv: array([[0.05023331]])
jac: array([4.76837158e-07])
message: 'Optimization terminated successfully.'
nfev: 15
nit: 3
njev: 5
status: 0
success: True
x: array([-1.67096375])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 1530
nit: 100
njev: 510
x: array([-1.67096375])
ネルダー – ミード アルゴリズム:
- Nelder-Mead アルゴリズムは、メソッド パラメータを介して選択します。
- 公正に振る舞う関数を最小化する最も簡単な方法を提供します。
- Nelder – ミード アルゴリズムは、解を見つけるのに時間がかかる可能性があるため、勾配評価には使用されません。
import numpy as np
from scipy.optimize import minimize
#define function f(x)
def f(x):
return .4*(1 - x[0])**2
optimize.minimize(f, [2, -1], method="Nelder-Mead")
出力:
final_simplex: (array([[ 1. , -1.27109375],
[ 1. , -1.27118835],
[ 1. , -1.27113762]]), array([0., 0., 0.]))
fun: 0.0
message: 'Optimization terminated successfully.'
nfev: 147
nit: 69
status: 0
success: True
x: array([ 1. , -1.27109375])
SciPy による画像処理 – scipy.ndimage
- scipy.ndimage は SciPy のサブモジュールで、主に画像関連の操作を実行するために使用されます
- ndimage は「n」次元の画像を意味します。
- SciPy 画像処理は、幾何学変換 (回転、切り抜き、反転)、画像フィルタリング (シャープおよびデノシング)、画像表示、画像セグメンテーション、分類、および特徴抽出を提供します。
- MISC パッケージ SciPy には、画像操作タスクの実行に使用できるビルド済みの画像が含まれています
例: 画像の幾何学的変換の例を見てみましょう
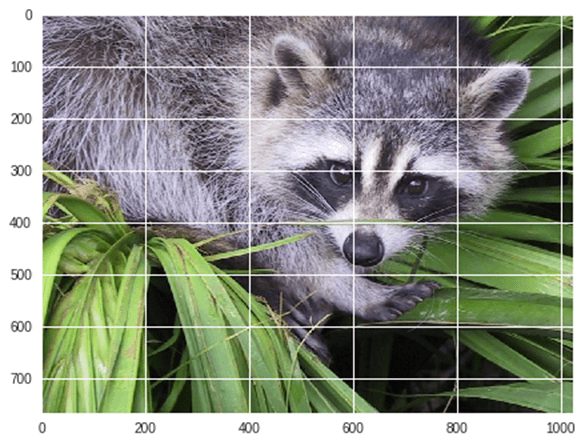
from scipy import misc from matplotlib import pyplot as plt import numpy as np #get face image of panda from misc package panda = misc.face() #plot or show image of face plt.imshow( panda ) plt.show()
出力:
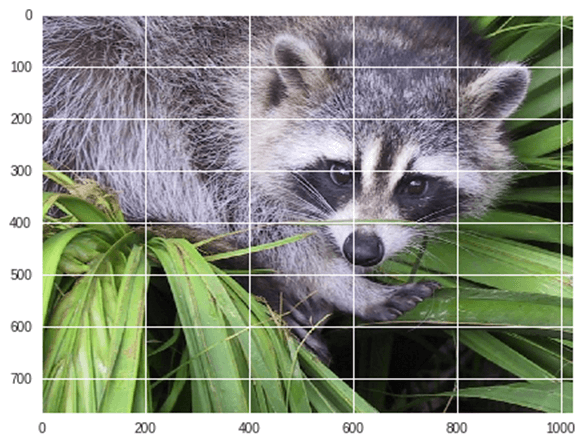
今度はフリップダウン 現在の画像:
#Flip Down using scipy misc.face image flip_down = np.flipud(misc.face()) plt.imshow(flip_down) plt.show()
出力:
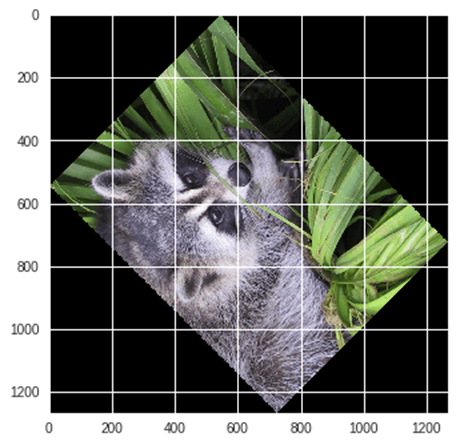
例: Scipy を使用した画像の回転
from scipy import ndimage, misc from matplotlib import pyplot as plt panda = misc.face() #rotatation function of scipy for image – image rotated 135 degree panda_rotate = ndimage.rotate(panda, 135) plt.imshow(panda_rotate) plt.show()
出力:
Scipy との統合 – 数値統合
- 解析的に統合できない関数を統合する場合は、数値統合を行う必要があります
- SciPy は関数を数値積分と統合する機能を提供します
- scipy.integrate ライブラリには、単一の積分、二重、三重、複数、ガウス四角形、Romberg、台形、およびシンプソンの規則があります。
例: 単一統合の例を見てみましょう
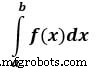
こちらが は上限で b は下限です
from scipy import integrate # take f(x) function as f f = lambda x : x**2 #single integration with a = 0 & b = 1 integration = integrate.quad(f, 0 , 1) print(integration)
出力:
(0.33333333333333337, 3.700743415417189e-15)
ここで、関数は 2 つの値を返します。最初の値は積分で、2 番目の値は積分の推定誤差です。
例:ここで、二重統合の SciPy の例を取り上げます。 次の方程式の二重積分を見つけます。
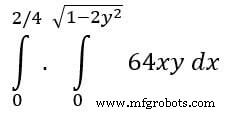
from scipy import integrate import numpy as np #import square root function from math lib from math import sqrt # set fuction f(x) f = lambda x, y : 64 *x*y # lower limit of second integral p = lambda x : 0 # upper limit of first integral q = lambda y : sqrt(1 - 2*y**2) # perform double integration integration = integrate.dblquad(f , 0 , 2/4, p, q) print(integration)
出力:
(3.0, 9.657432734515774e-14)
上記の出力は、前の出力と同じです。
まとめ
- SciPy (「Sigh Pi」と発音) は、オープン ソースの Python ベースのライブラリであり、数学、科学計算、工学、技術計算で使用されています。
- SciPy には、科学計算に関連する最も一般的な問題の解決に役立つさまざまなサブパッケージが含まれています。
- SciPy は NumPy の上に構築されています
| パッケージ名 | 説明 |
|---|---|
| scipy.io |
|
| scipy.special |
|
| scipy.linalg |
|
| scipy.interpolate |
|
| scipy.optimize |
|
| scipy.stats |
|
| scipy.integrate |
|
| scipy.fftpack |
|
| scipy.signal |
|
| scipy.ndimage |
|
Python
- Python Print() ステートメント:例を使用して印刷する方法
- 例を使用した Python 文字列 count()
- Python String format() 例で説明
- Python String find() メソッドと例
- 例を含む Python Lambda 関数
- Python abs() 関数:絶対値の例
- 例を使用した Python round() 関数
- 例を使用した Python map() 関数
- Python Timeit() と例
- Yield in Python チュートリアル:Generator &Yield vs Return の例
- Python の type() と isinstance() と例



