フーリエ変換とは何ですか？

この記事では、システム設計と信号処理で絶対的に基本的な役割を果たす数学的手法に関する重要な情報を提供します。

フランスの数学者ジョセフ・フーリエにちなんで名付けられたフーリエ変換は、周波数成分を決定するための数学的手順です。 関数の。電気技師の場合、フーリエ変換は通常、信号と呼ばれる時間の関数に適用されます。 。

正弦波分解

オシロスコープのディスプレイに表示されるように、電圧または電流と時間のプロットは、信号の動作を直感的に表したものです。ただし、これが唯一の有用な表現ではありません。

多くの場合、たとえばRFシステムの設計では、主に信号の周期的な動作に関心があります。より具体的には、正弦波に関する信号を理解することに関心があります。 正弦波は「純粋な」周波数のユニークな数式であるため、周期性。

フーリエ変換は、分解することにより、信号の要素の周期性を明らかにします。 信号をその構成正弦波周波数に変換し、これらの構成周波数の大きさと位相を識別します。

ここでは「分解する」という言葉が重要です。フーリエ変換は、時間領域信号を構成された波形として考えることを教えてくれます。 さまざまな大きさと位相を持つ基本的な正弦波形。

たとえば、方形波は、振幅が着実に減少し、周波数が着実に増加する無限の一連の正弦波に分解できます。周期Tおよび振幅AのAC結合方形波の正確な系列は、次のように記述できます。

\ [f_ {square}（t）=\ frac {4A} {\ pi} \ sum_ {k \ in {\ {1,3,5、... \ }}} \ frac {1} {k} \ sin \ left（\ frac {2 \ pi kt} {T} \ right）\]

これを次の形式に変換できます。これはもう少し直感的です：

\ [f_ {square}（t）=\ frac {4A} {\ pi} \ left（\ sin（2 \ pi ft）+ \ frac {1} {3 } \ sin（6 \ pi ft）+ \ frac {1} {5} \ sin（10 \ pi ft）+ \ ... \ right）\]

ここで、fは方形波の周波数（ヘルツ単位）です。

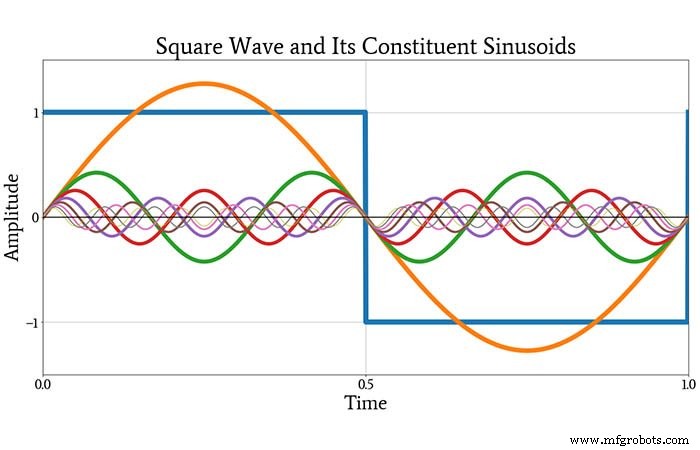
次のプロットは、元の方形波を青色で示し、無限級数の最初の8つの正弦波を示しています。

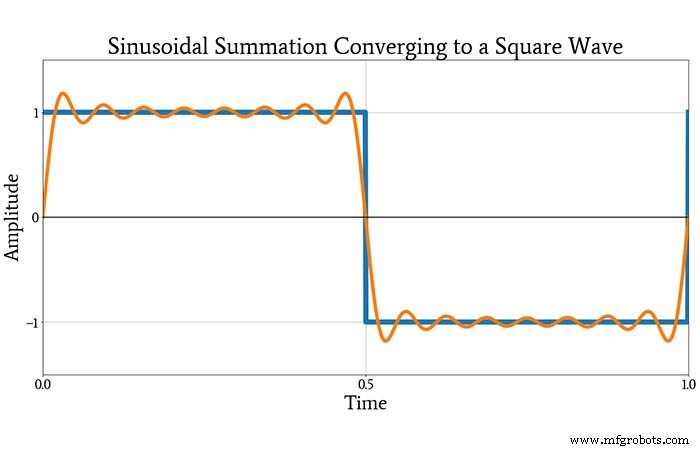
このプロットを見た後でも、これらの正弦波を組み合わせて方形波にすることができるかどうかについては少し懐疑的かもしれません。しかし、次のプロットはあなたを納得させるでしょう。元の方形波と追加によって生成された波形を示しています 上に示したすべての構成正弦波。

時間と頻度の関数

フーリエ変換を計算するときは、時間の関数f（t）から始め、数学的分解によって周波数の関数F（ω）を生成します。 （通常、フーリエ変換の理論的な議論では角周波数を使用します。）

ある特定の角周波数、たとえば100 rad / sでF（ω）を評価すると、100 rad / sの周波数を持つf（t）の正弦波成分の大きさと位相が得られます。 f（t）に100 rad / sの正弦波成分がない場合、大きさはゼロになります。

1つの関数F（ω）が大きさと位相の両方をどのように報告できるのか疑問に思われるかもしれません。フーリエ変換は複素数値を生成します 関数。つまり、変換自体は、f（t）の周波数成分の大きさでも、これらの成分の位相でもありません。他の複素数と同様に、大きさまたは位相を抽出するために追加の計算を実行する必要があります。

ディスクリートを使用する場合、複素数値変換の概念はやや直感的です。 時間の記号関数で始まり、周波数の記号関数で終わる「標準」変換ではなく、フーリエ変換。

離散フーリエ変換は一連の数値に作用し、一連のフーリエ係数を生成します。 。これらの係数は典型的な複素数であり（つまり、a + jbの形式を持ちます）、通常、√（a ² として計算されるこれらの複素数の大きさを使用します。 + b ² ）、信号の周波数成分を分析する場合。

フーリエ変換のプロット

頻度コンテンツのプロットは、データシート、テストレポート、教科書などで非常に一般的です。マグニチュードと周波数のプロットをスペクトルと呼ぶことがよくあります。たとえば、「信号のスペクトルを見てみましょう」とは、「フーリエ変換でマグニチュード情報のある種の視覚的表現を見てみましょう」という意味です。 。」

次のプロットは、振幅が1、周波数が1HzのAC結合方形波のスペクトルを示しています。

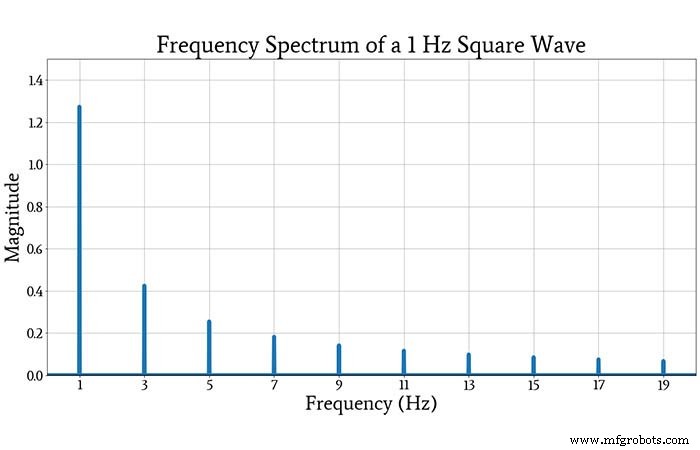
周波数「スパイク」のプロットされた振幅を、上記の無限級数の対応する正弦波成分の振幅と比較すると、それらが一貫していることがわかります。

フーリエ変換の計算

この記事はもうすぐ終わりですが、数学的に定義された信号のフーリエ変換を実際にどのように生成するかについては、まだ説明していません。

正直なところ、紹介記事で数学の詳細を徹底的に調査する必要はないと思います。今日の周波数領域分析は、ユーザーフレンドリーなソフトウェアベースの手法が主流であり、エンジニアはシンボリック時間の変換に多くの時間を費やしていません。ドメイン式をシンボリック周波数ドメイン式に変換します。

それでも、フーリエ変換と同じくらい重要なことを考えると、少なくとも基礎となる数学に注意するのは良いことです。したがって、これ以上苦労することなく、f（t）をF（ω）に変換する方法は次のとおりです。

\ [F（\ omega）=\ int \ Limits_ {-\ infty} ^ {+ \ infty} {f（t）{e ^ {--j \ omega t} } dt} \]

結論

この記事が、フーリエ変換とは何か、そしてそれが信号の性質についての追加の洞察をどのように提供するかについての明確で直感的な説明を提供したことを願っています。

フーリエ変換は、関連するトピックの広範な配列の始まりにすぎません。詳細については、以下の記事をご覧ください。

参考資料

• 離散フーリエ変換の概要
• 高速フーリエ変換の概要
• Scilabで周波数領域分析を実行する方法
• 周波数領域での生活を学ぶ
• 離散フーリエ変換に基づく線形フィルタリング