電圧計の設計

前に述べたように、ほとんどのメーターの動きは敏感なデバイスです。一部のダーソンバルムーブメントのフルスケール偏向電流定格はわずか50µAで、（内部）ワイヤ抵抗は1000Ω未満です。これにより、フルスケール定格がわずか50ミリボルト（50 µAX1000Ω）の電圧計になります。このような敏感な動きから実用的な（より高い電圧の）スケールを備えた電圧計を構築するには、測定された電圧量を動きが処理できるレベルまで下げる方法を見つける必要があります。

ダルソンバル運動計

フルスケールのたわみ定格が1mA、コイル抵抗が500ΩのD’Arsonvalメータームーブメントの問題例を始めましょう：

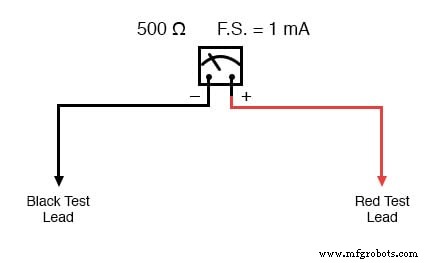
オームの法則（E =IR）を使用して、このメーターの動きを直接フルスケールに駆動する電圧を決定できます。

E =I R E =（1 mA）（500Ω） E =0.5ボルト

私たちが望んでいたのが1/2ボルトを測定できるメーターだけである場合、ここでの裸のメーターの動きで十分です。しかし、より高いレベルの電圧を測定するには、さらに何かが必要です。 1/2ボルトを超える有効な電圧計メーターの範囲を取得するには、測定された電圧の正確な割合のみがメーターの動き全体で降下するように回路を設計する必要があります。

これにより、メーターの動きの範囲がより高い電圧に拡張されます。これに対応して、このプロポーショニング回路を接続した新しい測定範囲を示すために、メーター面の目盛りにラベルを付け直す必要があります。

しかし、どのようにして必要なプロポーショニング回路を作成するのでしょうか？ええと、私たちの意図がこのメーターの動きでより大きな電圧を測定できるようにすることである場合 現在よりも、必要なのは分圧器 メーターの動きの接続ポイント全体で、測定された電圧の合計をより少ない割合に比例させる回路。分圧回路がシリーズから構築されていることを知っている 抵抗器、メーターの動きと直列に抵抗器を接続します（仕切りの2番目の抵抗器として動き自体の内部抵抗を使用します）：

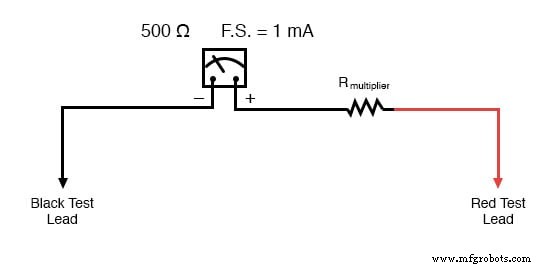
乗算器抵抗器

直列抵抗は、乗算されるため、「乗算器」抵抗と呼ばれます。 メーターの動きの動作範囲は、メーターの両端で測定された電圧を比例的に分割します。直列回路解析に精通している場合、必要な乗数抵抗値を決定するのは簡単な作業です。

たとえば、この1 mA、500Ωの動きが10ボルトの印加電圧で正確にフルスケールで読み取られるようにするために必要な乗数を決定しましょう。これを行うには、最初に2つのシリーズコンポーネントのE / I / Rテーブルを設定する必要があります。

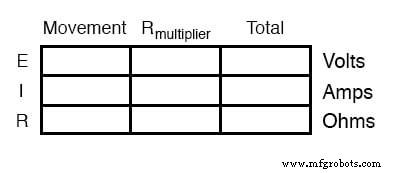
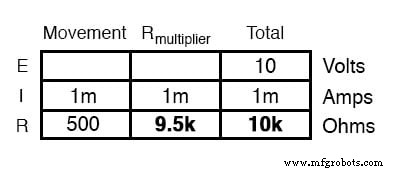
動きは1mAの電流が流れるフルスケールであり、これを10ボルトの印加（直列回路全体）電圧で発生させたいことを知っているので、次のように表に記入できます。

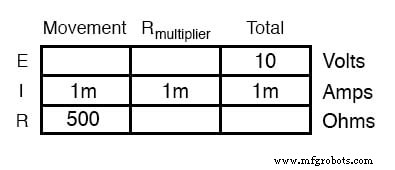
乗数の抵抗値を決定する方法はいくつかあります。 1つの方法は、「合計」列のオームの法則（R =E / I）を使用して合計回路抵抗を決定し、次に500Ωの移動を差し引いて乗数の値を算出することです。

同じ抵抗値を計算する別の方法は、フルスケール偏向（E =IR）での動作の両端の電圧降下を決定し、その電圧降下を合計から差し引いて、乗算器抵抗の両端の電圧に到達することです。最後に、オームの法則を再度使用して、乗数の抵抗（R =E / I）を決定できます。

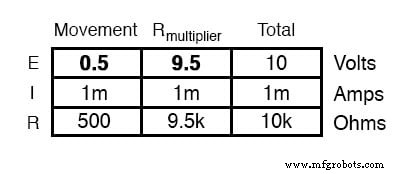
どちらの方法でも同じ答え（9.5kΩ）が得られ、一方の方法をもう一方の方法の検証として使用して、作業の正確さを確認できます。

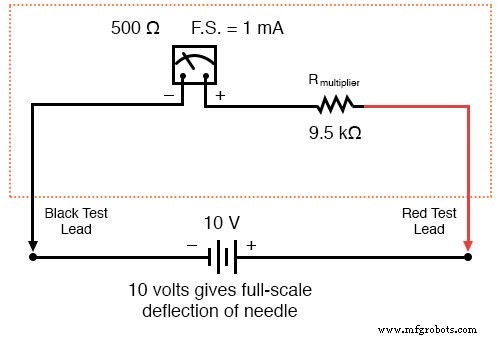
メーターのテストリード間に正確に10ボルトが印加されると（一部のバッテリーまたは精密電源から）、「乗数」抵抗とムーブメント自体の内部抵抗によって制限されるように、メーターの動きに正確に1mAの電流が流れます。ムーブメントのワイヤーコイルの抵抗を横切って正確に1/2ボルトが降下し、針が正確にフルスケールを指します。スケールにラベルを付け直して（0から1 mAではなく）0から10 Vまで読み取ると、スケールを表示する人は誰でもその表示を10ボルトと解釈します。

メーターのユーザーは、動き自体が実際には外部ソースからの10ボルトのほんの一部を測定していることにまったく気付く必要がないことに注意してください。ユーザーにとって重要なのは、回路全体が、印加された電圧の合計を正確に表示するように機能することです。

これが実用的な電気メーターの設計と使用方法です。高感度のメータームーブメントは、最大の感度を得るために可能な限り少ない電圧と電流で動作するように構築され、精密抵抗器で構築されたある種の分周器回路に「だまされ」ます。回路全体にはるかに大きな電圧または電流が印加された場合のフルスケールを示します。ここでは、単純な電圧計の設計を検討しました。電流計は、並列接続された「シャント」抵抗を使用して分流の法則を作成することを除いて、同じ一般的な規則に従います。 直列接続された分圧器とは対照的な回路 電圧計の設計に使用される「乗数」抵抗器。

一般に、このような電気機械式メーターには複数の範囲を設定しておくと、単一の移動メカニズムで広範囲の電圧を読み取ることができるので便利です。これは、多極スイッチといくつかの乗算器抵抗器を使用することで実現され、それぞれが特定の電圧範囲に合わせたサイズになっています。

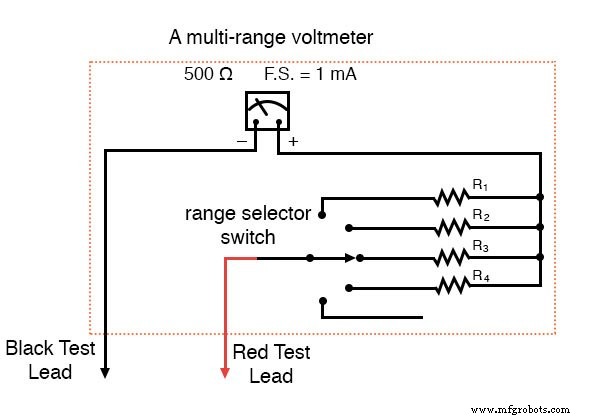
5ポジションスイッチは、一度に1つの抵抗器とのみ接触します。下部（時計回りいっぱい）の位置では、抵抗器とはまったく接触せず、「オフ」設定になります。各抵抗器は、電圧計に特定のフルスケール範囲を提供するようにサイズ設定されており、すべてメーターの動きの特定の定格（1 mA、500Ω）に基づいています。最終結果は、4つの異なるフルスケール測定範囲を備えた電圧計です。もちろん、これを適切に機能させるには、メーターのムーブメントの目盛りに各範囲に適したラベルを付ける必要があります。

このようなメーター設計では、各抵抗値は、既知の合計電圧、移動フルスケールたわみ定格、および移動抵抗を使用して、同じ手法で決定されます。 1ボルト、10ボルト、100ボルト、および1000ボルトの範囲の電圧計の場合、乗数抵抗は次のようになります。

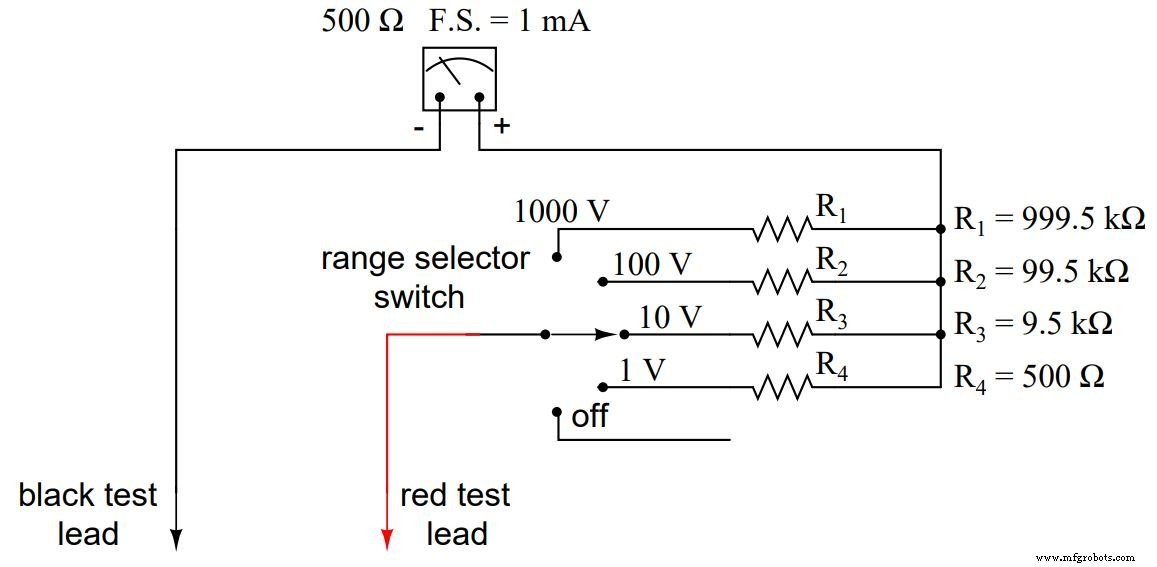
これらの範囲に使用される乗算器の抵抗値と、それらがどれほど奇妙であるかに注意してください。 999.5kΩの高精度抵抗が部品箱に見つかる可能性は非常に低いため、電圧計の設計者は、より一般的な抵抗値を使用する上記の設計のバリエーションを選択することがよくあります。

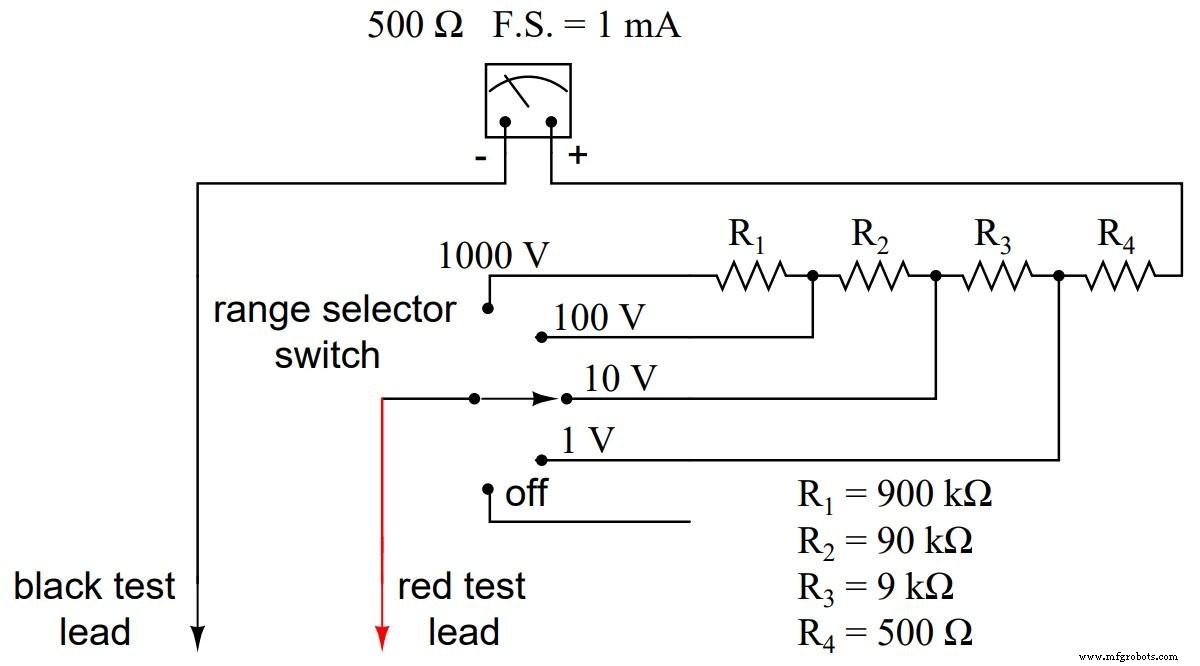
電圧範囲が連続的に高くなるたびに、セレクタスイッチによってより多くの乗算器抵抗が使用可能になり、それらの直列抵抗が必要な合計に追加されます。たとえば、レンジセレクタスイッチが1000ボルトの位置に設定されている場合、合計乗数抵抗値は999.5kΩである必要があります。このメーターの設計により、まさにそれが得られます：

R _合計 =R4 + R3 + R2 + R1 R _合計 =900kΩ+90kΩ+9kΩ+500Ω R _合計 =999.5kΩ

もちろん、利点は、個々の乗算器の抵抗値が、最初の設計のいくつかの奇数値（999.5k、99.5k、9.5k）よりも一般的（900k、90k、9k）であることです。ただし、メーターユーザーの観点からは、機能に認識できる違いはありません。

レビュー：

• 電圧計の範囲が拡張され、動きのある回路に直列の「乗数」抵抗を追加して、正確な分圧比を提供することにより、敏感なメーターの動きに対応します。

関連するワークシート：

• 電圧計設計ワークシート
• 電圧計ワークシート