量子化ノイズのパワースペクトルとは何ですか?
量子化ノイズに関するシリーズは、著者が量子化ノイズの調査範囲を決定するために使用したフレームワークの明確化から始まります。
このシリーズは、前の2つのシリーズで行われた作業の続きです。最初に、同相および直交(I / Q)の組み合わせと分離をアナログまたはデジタルで行う必要があるかどうかを調べました。 I / Q変調器と復調器、およびアナログ-デジタルコンバーター(ADC)とデジタル-アナログコンバーター(DAC)の性能を調べました。また、このコンテキストで通信リンクのパフォーマンスを向上させる理由についても説明しました。
ADCとDACはデータコンバータと呼ばれます。最新の通信波形に対するADCおよびDACのパフォーマンス要件に関する情報があまり見つからなかったため、作成者はこれらの問題を調査することにしました。 ADCとDACの適切なモデリングについては、ENOB(有効ビット数)とENOBに加えて相互変調多項式を利用するモデルの説明を含め、第2シリーズで説明しました。また、ローパスフィルターを含むさらに効果的なモデルに関する著者の提案についても検討しました。
シリーズの目標
データコンバータのパフォーマンスを調べると、多くの場合、図1に示す状況が見られます。
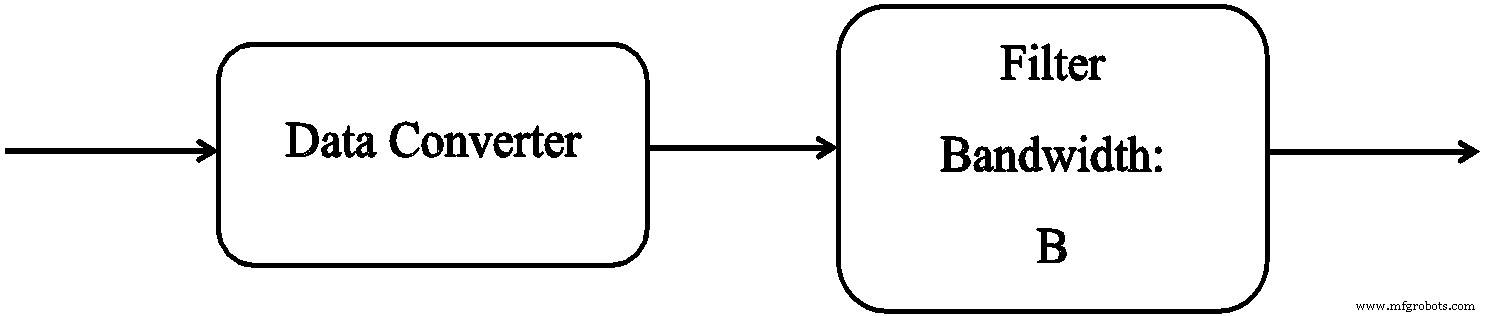
図1。 データコンバータの使用の簡略化されたブロック図
合計ノイズは、ナイキスト帯域幅(B N )でデータコンバーターをパワーアウトします。 )はNです。フィルターは帯域幅B o のバンドパスまたはローパスにすることができます。 。通常、フィルターからのノイズ電力は次のように想定されます。
式1。 この式は、任意の中心周波数で、ADCに続く可能性のある適切なフィルターにほぼ当てはまることに注意してください。 「合理的なフィルター」とは、狭すぎないフィルターです。
式1は、ノイズが白色、または周波数に対して均一であると想定しています。
あなたの作者は疑問に思いました。この仮定は、しばしば疑似量子化ノイズ[14]の仮定と呼ばれ、どのような条件下で本当ですか?
参考文献[3]から[32]は、この質問のさまざまな側面をカバーしています。物事を明確にするために、作成者はさまざまな入力を使用してデータコンバーターのシミュレーションも実行しました。結果はこのシリーズで報告されます。
彼は均一な量子化(すべてのステップサイズが等しい)のみを考慮しました。これは通常、高速データコンバーターで使用されるためです。また、シグマデルタコンバータは考慮されていません。
ADCアプリケーションの場合、多くの場合、RFチェーンゲインが十分に大きくなるため、前のコンポーネントからのノイズは量子化ノイズより3〜5 dB高くなるため、量子化ノイズスペクトルは重要ではありません。ただし、これにより、より多くのRFゲインと、ADCからのより高いダイナミックレンジが必要になるため、システムコストが増加する可能性があります。
DACアプリケーションの場合、DACからのノイズが支配的であり、送信されるノイズスペクトルが白であることを保証するためだけに、チェーンの後半にノイズを追加したくない場合があります。
ピーク、平均、およびrms値
入力信号のレベルを定義することが重要です。図2は、5ビットで量子化された正弦波を示しています。この信号のレベルは通常0dBFSと呼ばれます。ここで、FSは量子化器のフルスケールを指します。ただし、RFエンジニアは通常rms量を扱います。正弦波のrms値はピーク値より3dB低いため、図2の正弦波は-3 dBrmsFS、つまり0dBpeakFSになります。
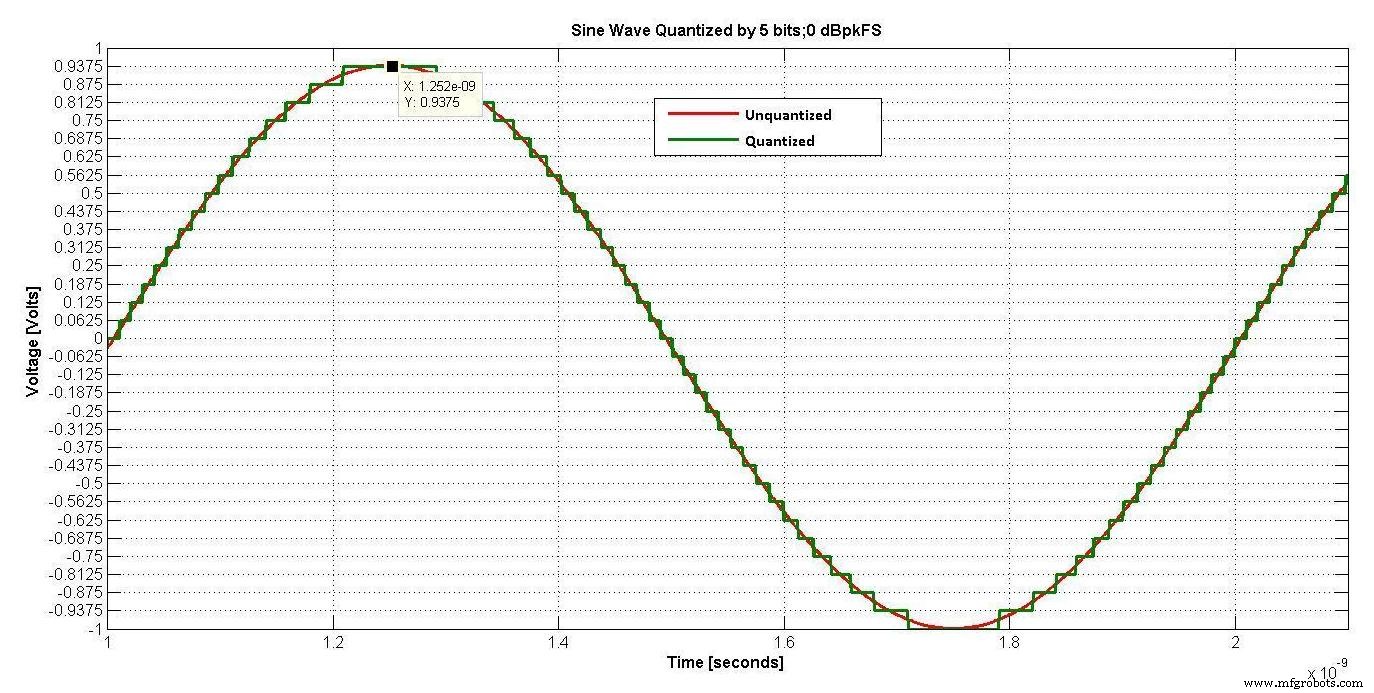
図2。
このシリーズの残りの部分では、信号レベルはdBrmsFSまたはdBpeakFSで指定されます。
また、電力は電圧の2乗であるため、この一定エンベロープ正弦波のピーク対平均電力比(PAPR)は3dBであることに注意してください。実際、MSKなどのすべてのバンドパス位相または周波数変調された一定エンベロープ信号のPAPRは3dBです。
"ちょっと待って!"あなたは言うかもしれません、親愛なる読者。 「MSKなどの一定エンベロープ信号のPAPRは0dBではありませんか?それは人々がそれを呼ぶものです。」
実際、人々がこのようにPAPRを参照するとき、彼らはエンベロープの平均パワーに対するエンベロープのピークパワーの比率を参照しています。特に、PAPRへのこの参照は、信号の複雑なエンベロープ[33]を特徴付けるときに使用されます。このシリーズでは実際の電圧に関係しているため、PAPRは実際のピークの電力を実際の平均の電力で割ったものになります。このPAPRは、通常引用されているものより3dB高くなります。
次の記事では、アナログ-デジタルコンバータ(ADC)出力のスペクトルについて説明します。
使用される略語
シリーズの残りの部分については、次の表を使用してください。
参考資料
次のリファレンスは、シリーズの残りの部分でも使用されます。
紹介と動機
[1]デジタルまたはアナログ? IとQの組み合わせと分離はどのように行う必要がありますか?
良好な通信リンクパフォーマンスの要件:IQ変調および復調
[2]システムシミュレーションのためにデータコンバータをどのようにモデル化する必要がありますか?
有効ビット数(ENOB)を使用したADCのモデリング
相互変調多項式と有効ビット数を使用したADCのモデリング
ADCモデルとDACモデリングへのローパスフィルターの追加
クリッピング効果の有無にかかわらず量子化ノイズ
ADCとDAC
[3]マロベルティ、フランコ;データコンバーター;シュプリンガーパブリッシング; 2007
ADC固有、クリッピング効果ありとなし
[4]レバー、K。V。; Cattermol、K.W。、「Quantising noiseスペクトル」、Electrical Engineers、Proceedings of the Institution of、vol.121、no.9、pp.945,954、1974年9月
レバー、K.V。; Cattermole、K.W。、「正誤表:ノイズスペクトルの定量化」、Electrical Engineers、Proceedings of the Institution of、vol.122、no.3、pp.272、1975年3月
[5] Gersho、A、「量子化の原理」、Circuits and Systems、IEEE Transactions on、vol.25、no.7、pp.427、436、1978年7月
[6] Gersho、A、「Quantization」、Communications Society Magazine、IEEE、vol.15、no.5、pp.16、16、1977年9月
[7] Schuchman、L。、「ディザ信号とその量子化ノイズへの影響」、Communication Technology、IEEE Transactions on、vol.12、no.4、pp.162、165、1964年12月
[8] Walden、R.H。、「アナログ-デジタルコンバーターおよび関連するICテクノロジー」、複合半導体集積回路シンポジウム、2008年。CSIC'08。 IEEE、vol。、no。、pp.1、2、2008年10月12〜15日
[9] Walden、R.H。、「アナログ-デジタルコンバータのパフォーマンストレンド」、Communications Magazine、IEEE、vol.37、no.2、pp.96、101、1999年2月
[10] Walden、RH、「アナログ-デジタルコンバータ技術の比較」、ガリウムヒ素集積回路(GaAs IC)シンポジウム、1994年、Technical Digest 1994.、第16回年次、vol。、no。、pp.217,219、16- 1994年10月19日
[11] Walden、R.H。、「アナログ-デジタル変換器の調査と分析」、通信の選択された領域、IEEE Journal on、vol.17、no.4、pp.539、550、1999年4月
[12] Morgan、DR、「A / D変換へのアプリケーションを使用した、帯域制限されたガウスランダムプロセスの有限制限効果」、音響、音声および信号処理、IEEE Transactions on、vol.36、no.7、pp.1011 、1016、1988年7月
[13] Chow、P.E.-K。、「波形量子化におけるパフォーマンス」、Communications、IEEE Transactions on、vol.40、no.11、pp.1737、1745、1992年11月
[14] Dardari、D。、「高速WLAN受信機におけるジョイントクリッピングおよび量子化効果の正確な分析」、Communications、2003年。ICC'03。 IEEE International Conference on、vol.5、no。、pp.3487、3492 vol.5、11-15 May 2003
[15]グレイ、R.M。、「量子化ノイズスペクトル」、情報理論、IEEE Transactions on、vol.36、no.6、pp.1220、1244、1990年11月
[16] Echard、J。; Watt、M.L。、「カラーノイズにおける正弦波の量子化ノイズスペクトル」、信号処理、IEEE Transactions on、vol.39、no.8、pp.1780、1787、1991年8月
[17]彼はジン;李ギャング; Xu Xibin; Yao Yan、「線形デジタルフィルタの量子化ノイズスペクトルの推定」、Communication Technology Proceedings、2000年。WCC-ICCT2000。InternationalConferenceon、vol.1、no。、pp.184、187 vol.1、2000
[18] Bennett、W.R。、 "Spectra of Quantized Signals"、Bell System Technical Journal、The、vol.27、no.3、pp.446、472、July 1948
[19] Mohamed、EM、「MIMO-Constant Envelope Modulationの低複雑度チャネル推定技術」、Wireless Technology and Applications(ISWTA)、2013 IEEE Symposium on、vol。、no。、pp.97、102、22-25Sept。 。2013
[20] Clavier、A G。;パンター、P。F。;グリーグ、D.D。、「パルスカウント変調システムの歪み」、American Institute of Electrical Engineers、Transactions of the、vol.66、no.1、pp.989、1005、1947年1月
DAC固有、クリッピング効果ありとなし
[21] Ling、W.A、 "Shaping Quantization Noise and Clipping Distortion in Direct-Detection Discrete Multitone、" Lightwave Technology、Journal of、vol.32、no.9、pp.1750、1758、May1、2014
クリッピング効果のみ。 ADCのみ
[22] Mazo、JE、「クリップされたDCバイアスのガウスノイズの漸近歪みスペクトル[光通信]」、Communications、IEEE Transactions on、vol.40、no.8、pp.1339、1344、1992年8月
[23] Dakhli、M.C。; Zayani、R。; Bouallegue、R。、「レイリーフェージングチャネル下のMIMO OFDMシステムでの多項式モデルを使用した非線形歪み効果とパフォーマンス分析の理論的特性評価と補償」、Computers and Communications(ISCC)、2013 IEEE Symposium on、vol。、no。、pp .000583,000587、2013年7月7-10日
[24] Dardari、D。; Tralli、V。; Vaccari、A、「OFDMシステムにおける非線形歪み効果の理論的特性」、Communications、IEEE Transactions on、vol.48、no.10、pp.1755、1764、2000年10月
[25] Giannetti、F。; Lottici、V。; Stupia、I、「MC-CDMA伝送における非線形歪みノイズの理論的特性」、パーソナル、屋内、およびモバイル無線通信、2006 IEEE 17th International Symposium on、vol。、no。、pp.1,5、11-14Sept。 2006
[26] Van Vleck、J.H。;ミドルトン、D。、「クリップされたノイズのスペクトル」、IEEEの議事録、vol.54、no.1、pp.2、19、1966年1月
その他の関連する数学的処理
[27] Ermolova、N.Y。; Haggman、S.-G。、「Bussgangの理論の複素数値信号への拡張」、Signal Processing Symposium、2004、NORSIG2004。Proceedingsofthe 6th Nordic、vol。、no。、pp.45、48、11- 2004年6月11日
[28] Requicha、Aristides A G、「量子化された確率変数の関数の期待値」、Communications、IEEE Transactions on、vol.21、no.7、pp.850,854、1973年7月
[29] Pirskanen、J。; Renfors、M。、「マルチモードモバイル端末の量子化とジッタの要件」、Communications、2001年。ICC2001、IEEE International Conference on、vol.4、no。、pp.1182、1186 vol.4、2001
[30]アイアン、フレッドH。;ライリー、K.J。;フンメル、D.M。; Friel、G.A、「ノイズ電力比-理論とADCテスト」、計測と測定、IEEE Transactions on、vol.49、no.3、pp.659,665、2000年6月
[31] Widrow、B。、「ナイキストサンプリング理論による大まかな振幅量子化の研究」、回路理論、IRE Transactions on、vol.3、no.4、pp.266、276、1956年12月
[32] Rowe、H.E。、「ガウス入力による無記憶非線形性:基本的な結果」、Bell System Technical Journal、The、vol.61、no.7、pp.1519、1525、1982年9月
[33] VanTrees、Harry L;検出、推定、および変調理論、パートIII、レーダー/ソナー信号処理およびノイズ中のガウス信号。 John Wiley and Sons; 1971.付録:「バンドパス信号、システム、およびプロセスの複雑な表現」AES-1、発行:6、1979、ページ:840〜848。
モノのインターネットテクノロジー



