コンダクタンス
学生が最初に並列抵抗方程式を見るとき、尋ねるべき自然な質問は、「それはどこで 何から来たの?」それは本当に奇妙な算術であり、その起源は良い説明に値します。
抵抗とコンダクタンスの違いは何ですか?
抵抗は、定義上、摩擦の尺度です。 コンポーネントは、それを通る電流の流れに現れます。抵抗は大文字の「R」で表され、「オーム」の単位で測定されます。ただし、この電気的特性は、その逆の観点から考えることもできます。簡単 難しいのではなく、電流がコンポーネントを流れるためです。 。
抵抗の場合 は、電流が流れるのがどれほど難しいかを表すために使用する言葉です。次に、電流が流れるのがどれほど簡単かを表すのに適した言葉は、コンダクタンスです。 。数学的には、コンダクタンスは抵抗の逆数または逆数です。
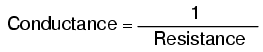
抵抗が大きいほど、コンダクタンスは小さくなります。その逆も同様です。
抵抗とコンダクタンスは同じ本質的な電気的特性を表す反対の方法であるため、これは直感的に理解できるはずです。
2つのコンポーネントの抵抗を比較し、コンポーネント「A」がコンポーネント「B」の半分の抵抗を持っていることがわかった場合、コンポーネント「A」は と言うことで、この関係を表すことができます。>> コンポーネント「B」と同じくらい導電性です。コンポーネント「A」の抵抗がコンポーネント「B」の3分の1しかない場合、 3倍と言えます。 コンポーネント「B」などよりも導電性が高い。
コンダクタンスの単位
この考えをさらに推し進め、コンダクタンスを表す記号と単位を作成しました。記号は大文字の「G」で、単位は mho 、これは逆に綴られた「オーム」です(そして、エレクトロニクスエンジニアがユーモアのセンスを持っているとは思わなかったでしょう!)
その適切性にもかかわらず、モーの単位は後年、ジーメンスの単位に置き換えられました。 (大文字の「S」で省略)。単位名を変更するというこの決定は、摂氏の温度単位からの変更を彷彿とさせます 度まで摂氏 、または頻度の単位からの変更 c.p.s。 (1秒あたりのサイクル数)からヘルツ 。ここでパターンを探している場合、シーメンス、摂氏、ヘルツはすべて有名な科学者の名前です。残念ながら、その名前は、ユニットの元の指定よりもユニットの性質について詳しく教えてくれません。
脚注として、ジーメンスの単位は最後の文字「s」なしで表現されることはありません。つまり、「オーム」や「モー」のように「ジーメンス」の単位というものはありません。この理由は、それぞれの科学者の名前の正しいつづりです。
電気抵抗の単位は「オーム」という名前の人にちなんで名付けられましたが、電気コンダクタンスの単位は「ジーメンス」という名前の人にちなんで名付けられました。したがって、最後の「s」は意味しないため、後者の単位を「特異化」することは不適切です。複数。
並列回路の例に戻ると、電流の複数のパス(分岐)によって回路全体の総抵抗が減少することがわかります。これは、電流が複数の分岐のネットワーク全体を流れることができるためです。それらの分岐抵抗だけです。 抵抗に関して 、ブランチを追加すると、合計が少なくなります(現在は反対が少なくなります)。 コンダクタンスに関して ただし、ブランチを追加すると、合計が大きくなります(コンダクタンスの大きい電流が流れます)。
総並列抵抗
総並列抵抗は少ない 並列抵抗は個別の抵抗よりも抵抗が少ないため、個々の分岐抵抗のいずれよりも抵抗が大きくなります。
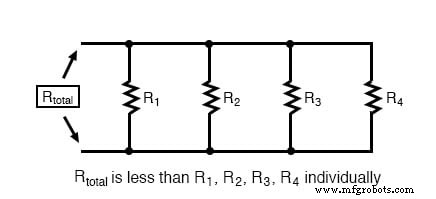
総並列コンダクタンス
総並列コンダクタンスはより大きい 並列抵抗は個別の抵抗よりも一緒に導通するため、個々の分岐コンダクタンスのいずれよりも優れています。
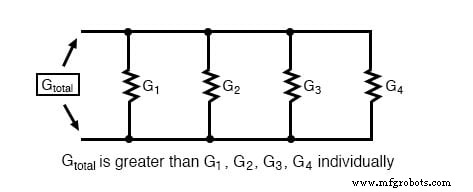
より正確には、並列回路の総コンダクタンスは、個々のコンダクタンスの合計に等しくなります。
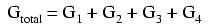
コンダクタンスが抵抗の数学的逆数(1 / x)にすぎないことがわかっている場合は、それぞれのコンダクタンスの逆数を代入することで、上記の式の各項を抵抗に変換できます。
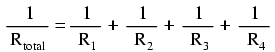
(総抵抗の逆数ではなく)総抵抗について上記の方程式を解くと、方程式の両辺を反転(往復)できます。
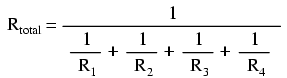
それで、私たちはついに私たちの不可解な抵抗式に到達します!コンダクタンス(G)が実際の測定値として使用されることはめったにないため、上記の式は並列回路の分析でよく見られる式です。
レビュー:
- コンダクタンスは抵抗の反対であり、簡単の尺度です。 何かに電流が流れるためです。
- コンダクタンスは文字「G」で表され、 mhos の単位で測定されます。 または Siemens 。
- 数学的には、コンダクタンスは抵抗の逆数に等しくなります:G =1 / R
関連するワークシート:
- オームの法則ワークシート
- 導体の比抵抗ワークシート
産業技術



