メッシュ解析とは：手順とその例

エレクトロニクスの分野では、単純な回路でさえ分析することがより重要です。単純な回路の解析には、キルヒホッフの電圧やキルヒホッフの現在の法則などの原理が使用されます。複数の制御された電圧および電流源を持つ複雑な回路の状況では、KVLおよびKCLの法則とともに追加のツールが必要です。 KVLとKCLの原則がある場合にのみ、分析は不正確で信頼性が低いことがわかります。したがって、正確な分析を行い、これらの回路の変数を知るには、メッシュやノードなどのアプローチを実装する必要があります。これらの方法を使用すると、電流や電圧などの変数を簡単に知ることができます。この記事では、メッシュ分析、スーパーメッシュ分析について明確にお知らせください。

メッシュ分析とは何ですか？

メッシュは、回路内に他のループがないループと見なされます。ここでは、回路解析全体を把握するために、電流の代わりにメッシュ電流を変数として使用しています。このため、この手法を解くには最小限の方程式が必要です。メッシュ分析は、キルヒホッフの電圧法則を使用して回路に実装され、未知の電流値を認識します。

これは、メッシュ電流ループ手法とも呼ばれます。この後、オームの法則を実行することで電圧値を知ることもできます。分岐は、2つのノードを接続するパスと見なされ、回路要素に含まれます。メッシュが1つの分岐のみで構成されている場合、分岐電流はメッシュ電流と呼ばれます。一方、メッシュが2つのブランチで構成されている場合、メッシュ電流は、2つのメッシュループが類似または反対のパスにある場合の合計または差と見なされます。

ステップ

• 回路の変数を知るには、メッシュ分析を実装するために従うべき手順があり、その手順は次のように説明できます。
• 最初のフェーズで、メッシュを見つけて、反時計回りまたは時計回りのいずれかの方向のメッシュ電流をマークします。
• メッシュ電流に対応する各要素を流れる電流の量を調べます。
• 観測されたメッシュのすべてのメッシュ方程式を書き留めます。メッシュ方程式は、キルヒホッフの法則を適用し、その後オームの法則を適用して記述されます。
• メッシュ電流を見つけるには、手順3に従って観測されたメッシュ方程式を解きます。
• これにより、メッシュ電流を適用することで、回路内のすべての要素に流れる電流と電圧の値を知ることができます。

メッシュ解析で方程式を設定するための一般的な形式

回路内のメッシュを特定すると、すべてが1つの方程式で構成されます。方程式は、メッシュ電流のループ全体での電圧降下の合計です。電圧と電流を超える回路の場合、電圧降下は回路のインピーダンスに特定のループメッシュ電流を掛けたものと見なされます。

電圧源がループの内部に存在する場合、電圧源に存在する電圧は、そのメッシュの電圧の損失であるか電圧の増加であるかという条件に基づいて、加算または減算することができます。ただし、電流源がメッシュの間にない状態では、メッシュ電流はメッシュ電流源の方向に基づいてソースの負または正の値を考慮します。

メッシュ電流法

以下の回路を使用すると、メッシュ電流法の解析を簡単に知ることができます。この回路では、ループ電流I1とI2が時計回りに流れています

ループ電流の方向に応じて、電圧降下の極性は抵抗R1、R2、およびR3で発生します。ここでは、抵抗R2が両方のループを共有しているため、I1電流とI2電流の電流経路は逆になります。

したがって、電圧の両方の極性を知ることができます。実際のシナリオでは、R2は2つのフェーズに分類できますが、ループ電流は特に分析アプリケーションに適用できます。電圧源は一定であるため、電圧源の極性に影響はありません。

キルヒホッフの電圧法則を適用すると、次の2つの方程式を書くことができます

R2（I1 – I2）+ R1I1 =V1 –ループ1から派生

R2（I2 – I1）+ R1I2 =-V2 –ループ2から派生

上記の方程式の同様の項が組み合わされ、配置されると、すべての方程式の同様の位置に同じ項が表示されます。ループ電流がわかっている場合は、分岐電流を評価できます。再配置された方程式は次のとおりです。

I1（R1 + R2）– I2R2 =V1 –Forループ1

-I1R2 +（R2 – R3）I3 =-V2 –ループ2の場合

メッシュ解析で解決された問題

このセクションでは、メッシュ電流法を使用して回路内の電流を検出するの解決例を示します。 。

以下の回路で、メッシュ解析の方法により、15アンペアの電流源を通過する電圧の量を調べます。すべてが現在のソースである場合

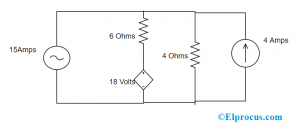
回路に従って、並列抵抗を使用して電圧源を電流に変更する可能性があります。これを行うには、抵抗器を電圧源と直列に接続し、抵抗器は電圧源と同じ値を持っている必要があり、電圧は

Vs =IsRs =4 * 4 =16V

ループの分岐電流（I1とI2）を調べて、両方のループの電流の流れの方向を示します。

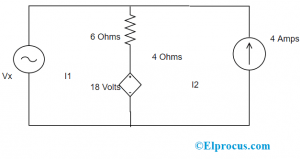
次に、すべてのメッシュ（ループ）に対して、KVLの法則を適用します

メッシュ– 1

Vx –（I1 – I2）– 18 =0

ここで、I1 =15

したがって、Vx +（6 * I2）=90

メッシュ– 2

18 – 6（I2 – I1）– 4 * I2 – 16 =0

I2 =78/10

=7.8アンペア

Mesh-1の式による

Vx =90 – 44.4

Vx =45.6 V

これは、メッシュ電流解析を使用して2つのメッシュを解くの解決例です。

ここでは、電圧と分岐電流を調べる必要があります。以下の回路を考えてみましょう。

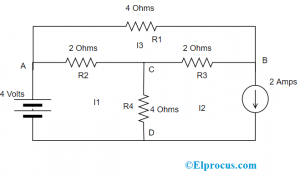
最初のループにKVLの法則を適用すると、次のようになります

V1 – R2（I1 – I3）– R4（I1 – I2）=0

4 – 2（I1）– 2（I3）– 4（I1）– 4（I2）=0

-2（I3）– 6（I1）=4

2番目のメッシュにKVLの法則を適用すると、次のようになります

-Vc – R4（I2 – I1）– R3（I2 – I3）=0

-Vc =-4（I1）+ 6（I2）– 2（I3）=0

I2 =-2Aであるため、次のようになります

-Vc =-4（I1）-12 – 2（I3）=0

3番目のメッシュにKVLの法則を適用すると、次のようになります

-R1（I3）– R3（I3 – I2）– R2（I3 – I1）=0

I2 =-2A

を代入する

2（I1）– 8（I3）=0

1番目と3番目のメッシュ方程式を解くと、次のようになります

I1 =4.46およびI3 =-0.615

したがって、Vc =28.61V

そして分岐電流は

Iac =I1 – I3

Iac =5.075アンペア

これは、メッシュ電流解析を使用して3つのメッシュを解決するの解決例です。

これらは、メッシュ分析によって解決されたサンプル例です。この概念を徹底的に分析することで、複雑な回路も解決できます。

スーパーメッシュ解析

巨大で複雑な回路の解析では、スーパーメッシュ解析がメッシュ解析よりも最適なアプローチとして機能します。スーパーメッシュには、電流源として共通のコンポーネントを共有する2つのメッシュがあるためです。

この方法では、電圧要素を閉じ、すべての電圧源の参照ノードの数を最小限に抑えることで、これらの複雑な回路を合理化するため、ノード回路解析の代替としてスーパーノード回路解析にも同じ手法が採用されます。スーパーメッシュ解析では、電流源はスーパーメッシュセクションの内側にあるため、存在する電流源ごとにメッシュを1つずつ最小化できます。

電流源が回路の許可器に存在する場合、単一のメッシュは考慮されない可能性があります。一方、KVLは、変更された電気回路のメッシュに対してのみ実装されます。

スーパーメッシュ解析の例について考えてみましょう。 理解を深めるために。

スーパーメッシュ解析を使用して、以下の回路のV3、i1、i2、およびi3の値を見つけますか？

KVLをMesh-1に適用すると、次のようになります

10i1 + 80（i1 – i2）+ 30（i1 – i3）=80

60i1 – 20i2 – 30i3 =80

を取得します

スーパーメッシュ手法をメッシュ2とメッシュ3に適用すると、次のようになります。

30 =40i3 + 30（i3 – i1）+ 20（i2 – i1）

70i3 – 50i1 + 20i2 =30

スーパーメッシュにある個々の電流源は、予想されるメッシュ電流に対応しています

15ix =i3 – i2

I3 =15ix + i2

上記の3つの方程式をすべて解くことにより、次のようになります。

i1 =0.58アンペア、i2 =-6.16アンペア、i3 =2.6アンペア

V3を見つけるには、v3 =i3 * R3なので、

V3 =2.6 * 40 =104V

メッシュ分析の使用

メッシュ解析の主な用途は、平面回路を解決して、単純な電気回路と複雑な電気回路の両方の任意の位置での電流値を知ることです。

もう1つの使用法は、方程式を解くための通常の計算が難しく、より多くの数式が必要になるのに対し、メッシュ分析では計算が少なくて済むことです。

メッシュ電流解析の他の使用法は、不均衡なホイートストンブリッジです。これを知るために、以下の例を検討してください

抵抗R1 / R4とR2 / R5の比率が等しくないため、R3にはある程度の電圧と電流が流れることがわかります。これらのタイプの回路の解決は、一般的な直並列技術のアプローチによって複雑になることを認識しているため、これを解決するには別のアプローチが必要です。

したがって、これに関しては、分岐電流法を適用することもできますが、この方法では、IaからIfまでの6つの電流が必要であり、これにより、任意の数の方程式が処理されます。したがって、この複雑さは、わずかな変数しか必要としないメッシュ電流法によって簡単に減らすことができます。