基本的なパーセプトロンニューラルネットワークをトレーニングする方法

この記事では、単純なニューラルネットワークの重みを自動的に生成できるPythonコードを紹介します。

パーセプトロンニューラルネットワークに関するAACのシリーズへようこそ。背景を最初から始めたり、先に進んだりする場合は、こちらの残りの記事をご覧ください：

1. ニューラルネットワークを使用して分類を実行する方法：パーセプトロンとは何ですか？
2. 単純なパーセプトロンニューラルネットワークの例を使用してデータを分類する方法
3. 基本的なパーセプトロンニューラルネットワークをトレーニングする方法
4. 単純なニューラルネットワークトレーニングを理解する
5. ニューラルネットワークのトレーニング理論の概要
6. ニューラルネットワークの学習率を理解する
7. 多層パーセプトロンを使用した高度な機械学習
8. シグモイド活性化関数：多層パーセプトロンニューラルネットワークでの活性化
9. 多層パーセプトロンニューラルネットワークをトレーニングする方法
10. 多層パーセプトロンのトレーニング式とバックプロパゲーションを理解する
11. Python実装のためのニューラルネットワークアーキテクチャ
12. Pythonで多層パーセプトロンニューラルネットワークを作成する方法
13. ニューラルネットワークを使用した信号処理：ニューラルネットワーク設計での検証
14. ニューラルネットワークのデータセットのトレーニング：Pythonニューラルネットワークをトレーニングおよび検証する方法

単層パーセプトロンによる分類

前回の記事では、ニューラルネットワークベースの信号処理の観点から検討した簡単な分類タスクを紹介しました。このタスクに必要な数学的関係は非常に単純だったため、特定の重みのセットによって出力ノードが入力データを正しく分類する方法を考えるだけで、ネットワークを設計できました。

これは私が設計したネットワークです：

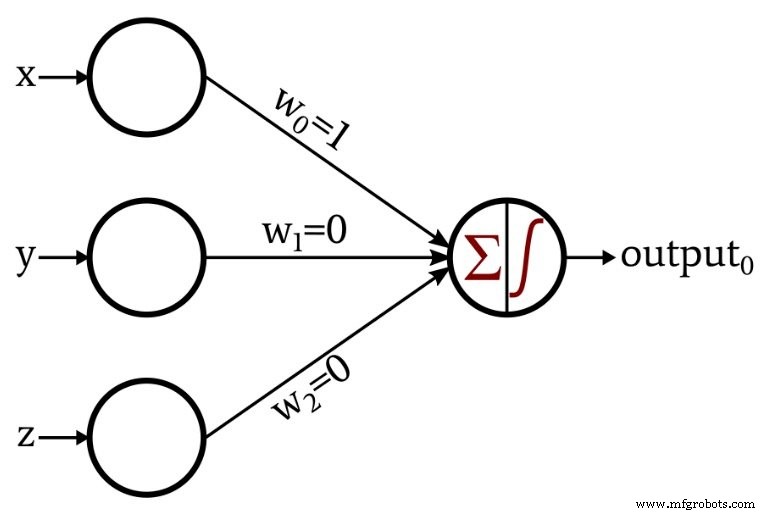
出力ノードの活性化関数は、単位ステップです：

\ [f（x）=\ begin {cases} 0＆x <0 \\ 1＆x \ geq 0 \ end {cases} \]

トレーニングと呼ばれる手順で独自の重みを作成するネットワークを提示したとき、議論はもう少し興味深いものになりました。

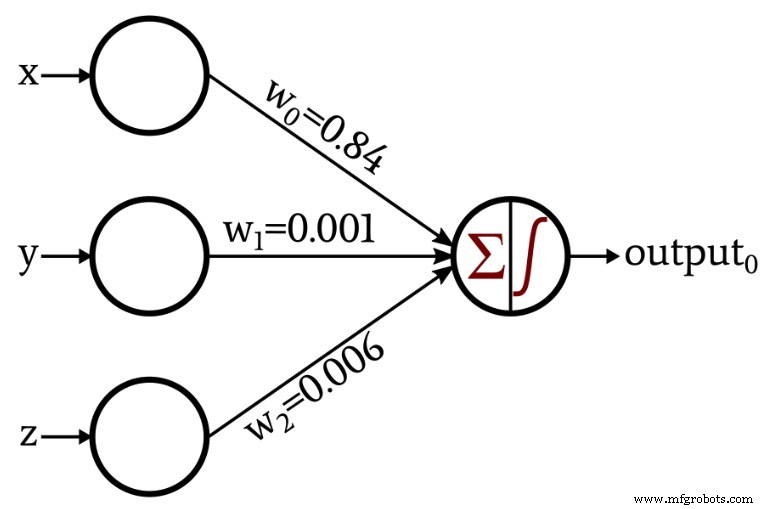
この記事の残りの部分では、これらの重みを取得するために使用したPythonコードを調べます。

Pythonニューラルネットワーク

コードは次のとおりです：

パンダのインポート numpyをnpとしてインポートします input_dim =3 Learning_rate =0.01 重み=np.random.rand（input_dim） #Weights [0] =0.5 #Weights [1] =0.5 #Weights [2] =0.5 Training_Data =pandas.read_excel（ "3D_data.xlsx"） Expected_Output =Training_Data.output Training_Data =Training_Data.drop（['output']、axis =1） Training_Data =np.asarray（Training_Data） training_count =len（Training_Data [：、0]） range（0,5）のエポックの場合： range（0、training_count）のデータムの場合： Output_Sum =np.sum（np.multiply（Training_Data [datum、：]、Weights）） Output_Sum <0の場合： Output_Value =0 それ以外： Output_Value =1 エラー=Expected_Output [データム] -Output_Value range（0、input_dim）のnの場合： Weights [n] =Weights [n] + Learning_rate * error * Training_Data [datum、n] print（ "w_0 =％。3f"％（Weights [0]）） print（ "w_1 =％。3f"％（Weights [1]）） print（ "w_2 =％。3f"％（Weights [2]））

これらの手順を詳しく見てみましょう。

ネットワークの構成とデータの整理

 input_dim =3 

寸法は調整可能です。入力データは、覚えていると思いますが、3次元座標で構成されているため、3つの入力ノードが必要です。このプログラムは複数の出力ノードをサポートしていませんが、調整可能な出力次元を将来の実験に組み込みます。

 Learning_rate =0.01 

学習率については、今後の記事で説明します。

 Weights =np.random.rand（input_dim） #Weights [0] =0.5 #Weights [1] =0.5 #Weights [2] =0.5 

重みは通常、ランダムな値に初期化されます。 numpy random.rand（）関数は、長さ input_dim の配列を生成します 間隔[0、1）に分散されたランダムな値が入力されます。ただし、初期の重み値は、トレーニング手順によって生成される最終的な重み値に影響を与えるため、他の変数（トレーニングセットのサイズや学習率など）の影響を評価する場合は、すべてを設定することでこの交絡因子を取り除くことができます。ランダムに生成された数値ではなく、既知の定数に重みを付けます。

 Training_Data =pandas.read_excel（ "3D_data.xlsx"）

パンダライブラリを使用して、Excelスプレッドシートからトレーニングデータをインポートします。次の記事では、トレーニングデータについて詳しく説明します。

 Expected_Output =Training_Data.output Training_Data =Training_Data.drop（['output']、axis =1）

トレーニングデータセットには、入力値と対応する出力値が含まれています。最初の命令は出力値を分離して別の配列に格納し、次の命令はトレーニングデータセットから出力値を削除します。

 Training_Data =np.asarray（Training_Data） training_count =len（Training_Data [：、0]）

現在パンダのデータ構造であるトレーニングデータセットをnumpy配列に変換し、列の1つの長さを調べて、トレーニングに使用できるデータポイントの数を決定します。

出力値の計算

 range（0,5）のエポックの場合：

1回のトレーニングセッションの長さは、利用可能なトレーニングデータの数によって決まります。ただし、同じデータセットを使用してネットワークを複数回トレーニングすることで、重みの最適化を継続できます。ネットワークがこれらのトレーニングデータをすでに認識しているという理由だけで、トレーニングのメリットが失われることはありません。トレーニングセット全体を完全に通過するたびに、エポックと呼ばれます。

 range（0、training_count）のデータムの場合：

このループに含まれる手順は、トレーニングセットの各行に対して1回発生します。ここで、「行」は、入力データ値と対応する出力値のグループを指します（この場合、入力グループはx、yを表す3つの数値で構成されます）。 、および3次元空間内の点のz成分）。

 Output_Sum =np.sum（np.multiply（Training_Data [datum、：]、Weights））

出力ノードは、3つの入力ノードによって提供される値を合計する必要があります。私のPython実装は、最初に Training_Data配列の要素ごとの乗算を実行することによってこれを行います。 および重量 配列を作成し、その乗算によって生成された配列内の要素の合計を計算します。

 Output_Sum <0の場合： Output_Value =0 それ以外： Output_Value =1 

if-elseステートメントは、ユニットステップのアクティブ化関数を適用します。合計がゼロ未満の場合、出力ノードによって生成される値は0です。合計がゼロ以上の場合、出力値は1です。

ウェイトの更新

最初の出力計算が完了すると、重み値が得られますが、ランダムに生成されるため、分類の達成には役立ちません。入力データと目的の出力値の間の数学的関係を徐々に反映するように重みを繰り返し変更することにより、ニューラルネットワークを効果的な分類システムに変えます。重みの変更は、トレーニングセットの各行に次の学習ルールを適用することで実現されます。

\ [w_ {new} =w +（\ alpha \ times（output_ {expected} -output_ {calculated}）\ times input）\]

記号 \（\ alpha \） 学習率を示します。したがって、新しい重み値を計算するには、対応する入力値に学習率と、期待される出力（トレーニングセットによって提供される）と計算された出力の差を乗算し、この乗算の結果を加算します。現在の重み値に。デルタを定義する場合（ \（\ delta \） ）as（\（output_ {expected} --output_ {calculated} \））、これを次のように書き換えることができます

\ [w_ {new} =w +（\ alpha \ times \ delta \ times input）\]

これが私がPythonで学習ルールを実装した方法です：

 error =Expected_Output [datum] -Output_Value range（0、input_dim）のnの場合： Weights [n] =Weights [n] + Learning_rate * error * Training_Data [datum、n] 

結論

これで、単一層、単一出力ノードのパーセプトロンのトレーニングに使用できるコードができました。次の記事では、ニューラルネットワークトレーニングの理論と実践について詳しく説明します。