複素数の紹介

2つの都市間の距離を説明する必要がある場合は、マイル、キロメートル、またはその他の線形測定単位で構成される1つの数値で構成される回答を提供できます。

ただし、ある都市から別の都市への移動方法を説明する場合、これら2つの都市間の距離だけでなく、より多くの情報を提供する必要があります。 方向に関する情報も提供する必要があります 旅行にも。

線形距離など、単一の次元を表す種類の情報は、スカラーと呼ばれます。 数学の量。スカラー数は、これまでのほとんどすべての数学アプリケーションで使用した種類の数です。

たとえば、バッテリーによって生成される電圧はスカラー量です。ワイヤーの抵抗（オーム）、またはワイヤーを流れる電流（アンペア）も同様です。

ただし、AC回路の分析を開始すると、電圧、電流、さらには抵抗（インピーダンスと呼ばれる）の量がわかります。 ACで）は、DC回路での測定に慣れているおなじみの1次元量ではありません。

むしろ、これらの量は動的であるため（方向と振幅が交互に）、考慮しなければならない他の次元を持っています。周波数と位相シフトは、これらの2つの側面に関係しています。

単一の周波数のみを扱う比較的単純なAC回路でも、振幅に加えて、対処すべき位相シフトの次元があります。

AC回路の分析を成功させるには、これらの多次元量を表現できる数学的対象と手法を使用する必要があります。

ここで、より適切なもののためにスカラー数を放棄する必要があります：複素数 。ある都市から別の都市への方向を示す例のように、単一周波数回路のAC量には、振幅（アナロジー：距離）と位相シフト（アナロジー：方向）の両方があります。

複素数は、振幅と位相シフトのこれら2つの次元を一度に表現できる単一の数学的な量です。

複素数のグラフィック表現

複素数は、グラフで表すとわかりやすくなります。特定の長さ（大きさ）と角度（方向）で線を引くと、物理学ではベクトルとして一般に知られている複素数のグラフィック表現が得られます。 ：(下の図）

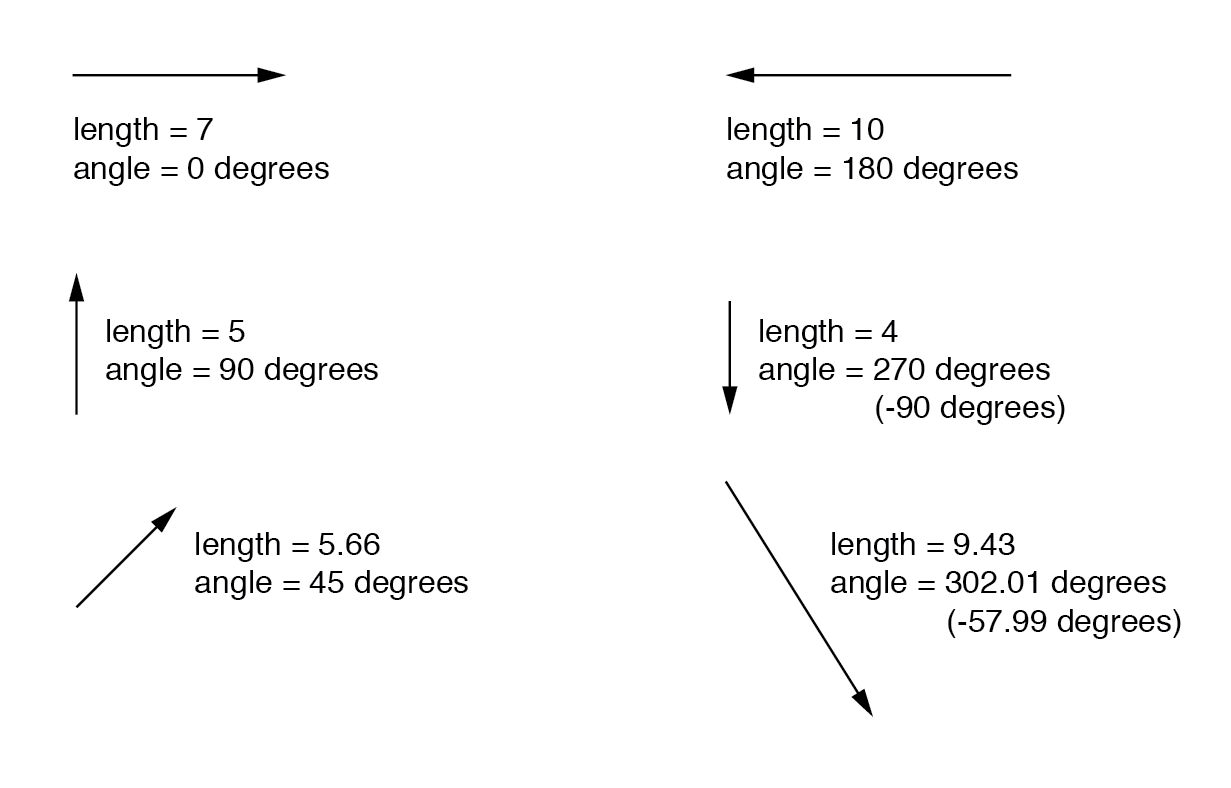
地図上の距離と方向として、角度の数値が意味を持つためには、いくつかの共通の基準枠が必要です。この場合、直接右は0 ^o と見なされます 、および角度は反時計回りに正の方向にカウントされます:(下の図）

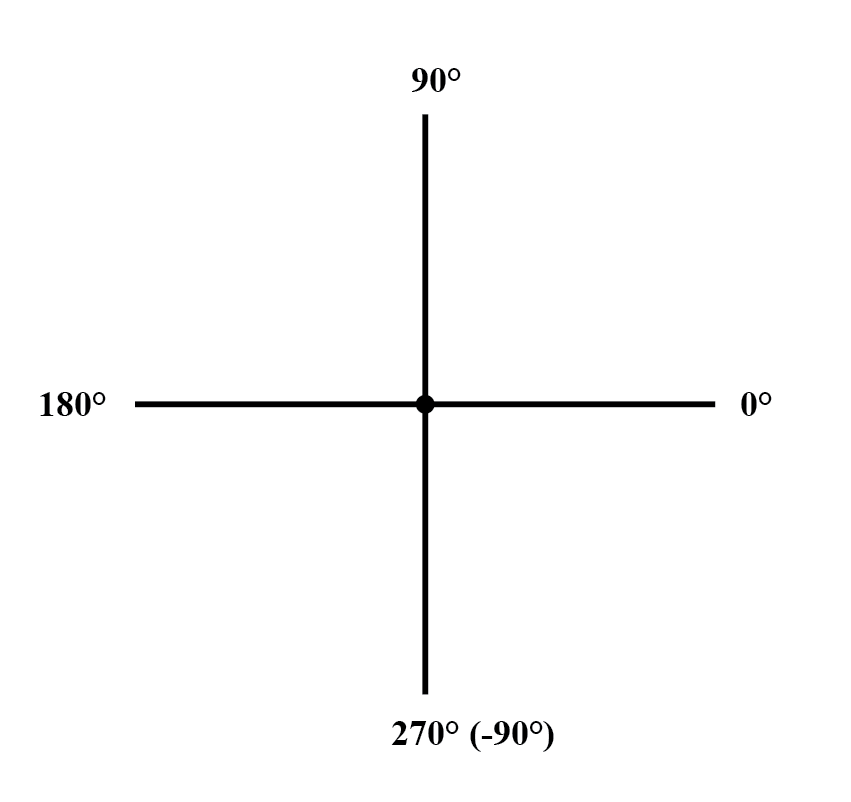
数値をグラフィック形式で表すという考え方は新しいものではありません。私たちは皆、小学校で「数直線」でこれを学びました:(下の図）

長さ（大きさ）がどのように積み重なって最終的な答えが得られるかを見て、足し算と引き算がどのように機能するかを学びました:(下の図）

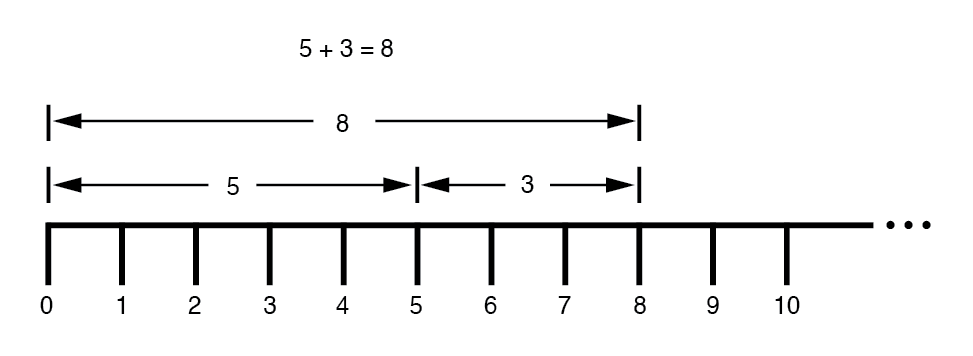
後で、 between の値を指定する方法があることを学びました。 行にマークされた整数。これらは小数または小数でした:(下の図）

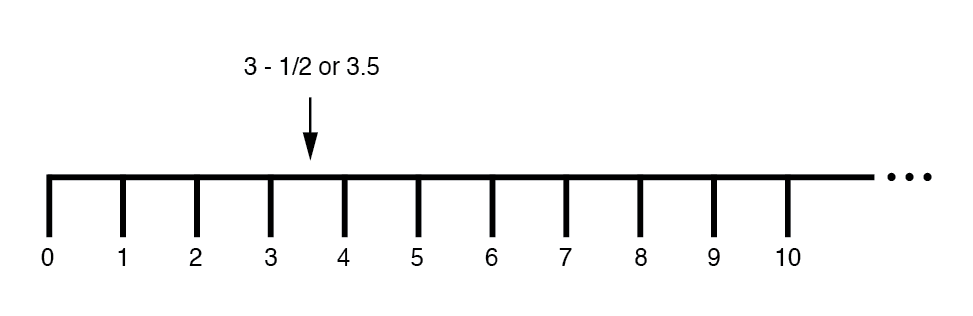
小学校で学んだこれらの数体（整数、有理数、無理数、実数など）は、共通の特徴を共有しています。これらはすべて一次元 。数直線の真直度は、これをグラフィカルに示しています。

数直線を上下に移動できますが、その線に沿ったすべての「動き」は1つの軸（水平）に制限されます。

1次元のスカラー数は、ビーズを数えたり、重量を表したり、DCバッテリー電圧を測定したりするのに完全に適していますが、距離や距離などのより複雑なものを表すには不十分です。 2つの都市間の方向、または振幅と AC波形の位相。

これらの種類の量を表現するには、多次元表現が必要です。言い換えれば、さまざまな方向を指すことができる数直線が必要であり、それがまさにベクトルです。

レビュー：

• スカラー 数は、人々が日常生活で使用するのに慣れている数学的対象のタイプです。温度、長さ、重量などの1次元量です。
• 複素数 は、大きさと方向の2つの次元を表す数学的量です。
• ベクトル 複素数のグラフィック表現です。矢印のように見え、始点、先端、明確な長さ、明確な方向があります。 フェーザという単語が ベクトルの角度が波形間の位相シフトを表す電気アプリケーションで使用されます。

関連ワークシート：

• ACフェーズワークシート