バイオインスパイアードナノポアにおける水の自己拡散係数からの溶媒和生体分子またはナノ粒子のナノメータリング

背景

水質モニタリング技術の必要性には、古くからの起源があります[1]。古代ローマでは、水源は人や動物の死体からの生物学的汚染物質や風呂からの廃水、鉛などの非生物学的汚染物質によって頻繁に汚染され[2]、深刻な病気や精神的な問題を引き起こしていました。何世紀にもわたる継続的な研究と進歩により、今日、世界のほとんどの人々が安全に飲める水道水を利用できるようになっています。それでもなお、8億5000万人以上がきれいな水への主要なアクセスを欠いています[3]。

多くの場合低濃度の水を汚染する可能性のある汚染物質の性質が異なるため、正確な品質監視は困難な作業です。特に、医薬品、化学物質、ナノマテリアルなどの微量レベルの新たな汚染物質のかなりの数は、環境や人間の健康に悪影響を与える可能性はありますが、既存の水処理プラントでは一般に監視および除去されていません[4]。 [5]。

過去数十年の間に、ナノテクノロジーの出現により、病原体、有機化学物質、無機化学物質など、水中のさまざまな汚染物質を検出するための調整された分子センサーの設計が可能になりました[6]。最も基本的なバージョンでは、これらのセンサーは、ナノ構造の材料、認識のための解析要素、および取得した情報を渡すためのアクティブなメカニズムで構成されています[7]。定量的な情報が取得されない場合、これらのシステムはむしろナノプローブ[8]と呼ばれ、化学物質を選択的に検出するために機能化された材料にも依存します。

生物医学の分野では、低濃度の生体分子の検出は、診断の精度を向上させ、患者のニーズに合わせて治療や薬を調整するために重要です。低濃度の生体分子の検出信号を増幅するために、さまざまな物理的および化学的現象に依存する超高感度の識別方法がこの目的のために開発されました[9–11]。

このフレームワークでは、ナノポーラス材料は、ボイドとチャネルを特徴とする独特の構造のために大きな注目を集めており、触媒作用[12]、吸着蓄熱[13]、分子などの多くのナノテクノロジーアプリケーションに特に適しています。ふるい分け[14]、選択的輸送（膜）[15]、ナノモーション[16]、ドラッグデリバリー[17]、および生体吸着[18]。

自然は、特定の機能を備えた効率的な階層的多孔質構造の優れた例を提供するため、これらのアプリケーションの開発に大きな影響を与えました[19、20]。インシリコ最適化と適切に設計された合成により、必要なアプリケーションの安定性が低く、過酷な環境への耐性が低いなど、考えられる制限を克服できます[21、22]。

珪藻の外骨格（フラスチュール）からインスピレーションを得て[23]、この研究では、水中の生体分子とナノ粒子のいくつかのクラスの濃度について、ナノポーラス計量タブレットを概念化します。重要なアイデアは、水分子がバルクおよびナノ閉じ込め条件、たとえばシリカナノポアで示すさまざまな自己拡散係数に依存することです。実際にナノ閉じ込めされると、水分子の移動度が低下し、拡散の余地が減少します。ナノ粒子や生体分子などの分子溶質の存在は、細孔のサイズと形状に加えて、そのサイズと性質に応じて移動度をさらに低下させます。この振る舞いは、以前に文献[24]で紹介されたスケーリング則によって正確に回復できます。したがって、ナノポア内の水の自己拡散係数により、そこに含まれる生体分子またはナノ粒子の濃度を間接的に定量化できることを示しています。シリカナノポア内のさまざまな濃度のタンパク質と酸化鉄ナノ粒子の分子動力学によって得られた結果は、提案された概念が満足のいく精度でそれらの濃度に関する明確な洞察をもたらすことを示しています。

仮説の提示

バイオインスパイアードナノメータリングのコンセプト

珪藻は、遍在する水性環境に生息する単細胞微生物（真核生物）です。それらの細胞は2つに分割され、二酸化ケイ素の殻（フラスチュール）に囲まれています。この多孔質マトリックス（外骨格）により、生細胞が外部環境と相互作用し、親水性表面と高い表面積対体積比を介してナノ粒子と活性生体分子の付着が最適化されます[23]。多孔質マトリックスのナノポアとスリットは、その化学的特性とともに、さまざまな用途向けの多数のナノテクノロジーデバイスのバイオインスパイアード設計に使用できます[25]。

珪藻の構造に基づいて、ここでは、水中のナノ粒子と生体分子のいくつかのクラスのナノ計量シリカ錠剤を概念化します。図1aは、中心珪藻 Thalassiosira pseudonana の走査型電子顕微鏡を示しています。 [26]。バルブは、チャネルによって特徴付けられる多孔質構造で構成されており、その直径は数ナノメートルのオーダーであり、この場合は特に約10 nmです（挿入図の詳細図を参照）。そのような規則的な多孔質構造の1つは、細孔サイズよりも大きい分子の自然なふるいを表しますが、それでも小さい分子の侵入を可能にし、ナノメータリングの概念に利用できる閉じ込め環境を提供します。

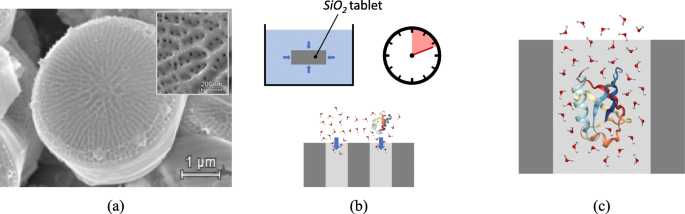
ナノメータリングシリカ錠剤のバイオインスパイアード概念化。 a Thalassiosira pseudonana の走査型電子顕微鏡 、バルブ全体とインサート内の多孔質ナノチャネルの詳細を示しています。 [26]から改作され、CC BY4.0ライセンスの下で使用されている画像。 b 最初は空のナノポアから始めて、水分子と溶媒和タンパク質は、特徴的な充填時間でシリカナノタブレットに侵入する傾向があります。 c シリカナノポアへのユビキチン（1UBQ）の侵入の詳細。タンパク質およびナノポア表面との静電相互作用により、水分子の移動度が低下します。

珪藻多孔質構造、または人工合成によって得られた同様の構造[27]が汚染物質を懸濁した水サンプルに浸されると、後者は毛細管現象と濃度勾配によって多孔質チャネルに移動します。平衡状態になるまで図1bを参照してください。に達した。ナノポアの内部では、ポアの表面と侵入したナノ粒子によって提供されるナノ閉じ込めのために、水分子の移動度が低下しています。結果として、ナノポア内の水の自己拡散係数は、バルクの自己拡散係数に比べて減少します。図1cを参照してください。ナノポアにおけるこの後者の自己拡散係数の知識は、例えば、拡散磁気共鳴画像法（D-MRI）[28、29]または準弾性中性子散乱（QENS）技術[30、31]を介して取得できます。 ]、次のセクションで説明する手順を介して汚染物質の濃度を推測することができます。

水の自己拡散係数による粒子濃度

固体表面の近くでは、水分子はファンデルワールスとクーロンの相互作用の影響を受けます。したがって、それらはバルク条件に関して異なる振る舞いを示します[32、33]。特に、これらの固液相互作用は、固体表面に近い水分子の層化を誘発し、それにより、それらの移動度が低下し、したがって、バルク状態に対する自己拡散係数が低下します。

この効果を含む水の自己拡散係数を予測するためのスケーリング則が[24]

ここで D _B および D _C は、それぞれバルク条件と完全にナノ閉じ込められた条件での水の自己拡散係数です。式で。 （1）、θ は、固体表面の形状と化学的特性に影響されるスケーリングパラメータであり、考慮される構成でのナノ閉じ込め水量と総水量の比率、つまりθです。 = V _c / V _tot 。特に、水がナノ閉じ込めされている特定の構成を考えると、 V _c 固液相互作用によって移動度が大幅に変化する水の量を表し、 V _tot 水がアクセスできる総量。ナノ閉じ込め水量 V _c i の合計として定義できます 溶媒にアクセス可能な表面 S A S _i 与えられたシステムに平均特性距離\（\ bar {\ delta} _ {i} \）を掛けると、それを下回ると水分子は i によって生成されるポテンシャル井戸の影響を大きく受けます。 固体表面、すなわち：

N であること システム内のさまざまな固液界面の数。特定の固体表面によって発揮される水のナノ閉じ込めの平均特性長\（\ bar {\ delta} _ {i} \）は、表面の幾何学的および化学的特性がわかれば、原子シミュレーションから簡単に推定できます[24、34 ]。ナノ粒子で満たされたナノポアの場合など、いくつかの固液界面が存在する場合、ナノ閉じ込め水量の部分的な重複が発生する可能性があることに注意してください。この場合、スケーリングパラメータθ 式で。 （1）は明らかであり、1より大きい値を取る可能性があるため、ナノ閉じ込め水の実際の割合を過大評価しています。この効果は、連続体パーコレーション理論（CPT）[35]によって考慮に入れることができます。これは、[24]

したがって、閉じ込めボリューム間の大きなオーバーラップの場合の水のナノ閉じ込めのより正確な推定は、θによって取得できます。 ^∗ したがって、これは式（1）でより適切に使用する必要があります。 （1）θの代わりに 。明らかに、θ ^∗ ≈θ θの場合 →0。

溶媒和ナノ粒子（または生体分子）の溶媒接触可能表面が S に等しい場合 A S _i 、式（2）を使用して、各ナノ粒子（または生体分子）あたりの平均ナノ閉じ込め水量を\（V _ {\ text {c} _ {\ text {i}}} ={SAS} _ {i} \、\バー{\ delta} _ {i} \）。これにより、浮遊ナノ粒子の数が\（\ phantom {\ dot {i} \！} n_ {i} =V _ {\ text {c}} / V _ {\ text {c} _ {\ text {i} }} \）、したがって、それらの数の集中。最終的に、質量に関する濃度は、考慮される種のモル質量を介して取得できます。

式1は、最初に原子シミュレーションから得られ、磁気共鳴画像法（MRI）実験に対して検証されました[24]。続いて、QENS測定[30、31]によっても検証され、固液界面での水のさまざまな特性を解釈するために適用されました[32、36]。

分子動力学

シミュレーションは、式（1）の有効性を実証するために実行されます。 （1）水和したナノポア内の水の自己拡散係数を考慮して、その中のナノ粒子または生体分子の濃度を推測する。分子動力学（MD）シミュレーションには、オープンソースソフトウェアGROMACS [37]が採用されています。バルク条件とナノ閉じ込め条件での水の移動度の違いを分析するために、2つの異なる幾何学的レイアウトが分析されます。バルク条件では、3つのデカルト軸に沿って周期性が適用される立方計算ボックスが採用されています。ナノ閉じ込め条件の場合、単一の円筒形ナノポアからなる、ナノメータリングシリカ錠剤のポアの簡略化された表現が採用されます（図1cを参照）。簡単にするために、一般性を失うことなく、規則的な細孔形状/サイズ分布が想定されているため、軸に沿って周期性が適用されます。

検討対象のタンパク質（ユビキチン-1UBQ;鶏卵白リゾチーム-1AKI）のジオメトリファイルはProtein Data Bank [38]データベースから取得しましたが、シリカナノポアとマグネタイトナノ粒子の両方は以前の研究[24]から入手できました。シリカナノポアと酸化鉄ナノ粒子の分子内結合相互作用は、[24]に詳述されているように、調和伸縮と角度ポテンシャルによってモデル化されます。それらの非結合相互作用は、[24]でも報告されているように、12-6レナードジョーンズと静電ポテンシャルによってモデル化されます。タンパク質の結合および非結合相互作用は、GROMOS96 43a2 [39]から取得されます。平衡化中、タンパク質のすべての結合は、LINCS（Linear Constraint Solver）アルゴリズムを使用して固定されていることに注意してください[40]。剛結合相互作用を伴うSPC / E水モデル[41]は、室温で水の最も関連性の高い特性を正確に回復するため、すべての場合に採用されます[42]。

バルク構成とナノ閉じ込め構成の両方で、システムは最初にエネルギーが最小化され、溶媒和されます（水密度は約1.00 g / cm ³ に等しい） ）そして、タンパク質の場合、正味電荷はイオン添加によって中和されます。詳細には、リゾチームの正味の正電荷を中和するために塩化物イオンがシミュレーションボックスに導入されますが、ユビキチンは中性であるため、イオンの追加は必要ありません。次に、水和システムは十分な時間、そのエネルギー最小値まで緩和されます。次に、システムの温度は、100 ps（ T ）のNVTアンサンブルでのシミュレーションによって平衡化されます。 =300 K、Nosé-Hooverサーモスタット）を使用して、シミュレートされた構成で位置エネルギーの収束を実現します（平衡値の周囲で約±1％の変動、追加ファイル1：図S1cを参照）。その後、バルク構成も100 ps（ T ）のNPTアンサンブルで平衡化されます。 =300 K、Nosé-Hooverサーモスタット; p =1バール、Parrinello-Rahmanバロスタット）、シミュレートされたセットアップで水密度の収束を達成します（平衡値の周りの約±2％の変動、追加ファイル1：図S1aを参照）。最終的に、本番稼働はNVTアンサンブル（ T ）で実行されます。 =300 K、Nosé-Hooverサーモスタット）。シミュレートされたすべてのケースで、100 psごとに評価される自己拡散係数が漸近値（つまり、移動平均の周りの±10％の変動、追加ファイル1：図S1bおよびd）。これは通常、バルク構成の場合は約500 ps、ナノ閉じ込め構成の場合は約1000 ps後に達成されるため、前者は1 nsまで継続され、後者は2nsまで継続されて統計が向上します。すべての実行で、タイムステップ0.001 psのリープフロッグアルゴリズムが使用され、ファンデルワールス相互作用には1.2 nmのカットオフ距離が採用され、静電相互作用には粒子メッシュエヴァルト（PME）法が採用されています（メッシュ間隔）。 0.16 nm）。固体ナノオブジェクトの溶媒接触可能表面は、生産実行から取得され、専用ルーチン（[24]の補足ソフトウェアを参照）に供給されます。このルーチンは、採用された力場に基づいて、ナノ閉じ込めの平均特性長を計算します。 （\ bar {\ delta} _ {i} \）各 i セットアップの固液界面。

仮説のテスト

さまざまなシステムの水の自己拡散

式のスケーリング則の有効性。 （1）は、文献（14構成）と新しいシミュレーション（9構成）の両方の結果を考慮して最初にテストされました。特に、文献から得られた構成は、直径 d の水和シリカナノポアです。 _P =8.13または11.04nm（[24]の補足表S1を参照）。直径 d の唯一のマグネタイトナノ粒子 _p =1.27または1.97nmを、それぞれ6または7 nmの側面を持つ立方体のウォーターボックスに浸します（[24]の補足表S4を参照）。それぞれ7.03または6.32nm側の立方体のウォーターボックスに浸された唯一の1AKIまたは1UBQタンパク質（[24]の補足表S10を参照）。直径 d の水和シリカナノポア _P =直径 d の2、4、8、または16個のマグネタイトナノ粒子で満たされた8.13 nm _p =1.97 nm（[24]の補足表S2を参照）または直径 d の16個のマグネタイトナノ粒子 _p =1.27 nm（[24]の補足表S3を参照）。直径 d の水和シリカナノポア _P =直径 d の36または66個のマグネタイトナノ粒子で満たされた11.04nm _p =1.27nmまたは直径 d のマグネタイトナノ粒子20個 _p =1.97 nm（[24]の補足表S3を参照）。さらに、新しいシミュレートされたセットアップは、直径 d の水和シリカナノポアです。 _P =8.13 nmは、1つの1UBQタンパク質と、直径 d の水和シリカナノポアで満たされています。 _P =11.04 nmは、2、3、または9個の1AKIタンパク質、または2、7、9、または12個の1UBQタンパク質で満たされています。

図2は、前述のさまざまなシステム、つまりバルク水（ D ）の水の自己拡散係数のスケーリング動作を示しています。 _B =2.60×10 ⁻⁹ m ² / s）、水和シリカナノポア、溶媒和タンパク質およびマグネタイトナノ粒子、およびタンパク質またはナノ粒子で満たされた水和シリカナノポア。予想通り、シリカナノポア内の水は、スケーリングパラメータθで表されるナノ閉じ込めの程度の増加と一貫して、自己拡散の減少を示します。 ^∗ 。浮遊分子（ナノ粒子とタンパク質）は、水の自己拡散係数に対して同様の効果を示します。図2では、実線は式（1）に対応します。 （1） D を使用 _C / D _B ≈0。これは、ナノ閉じ込め水分子に移動性がなく、したがって拡散できないと仮定する場合の限定的なケースを表します。代わりに、破線は、より現実的な値が D の同じ方程式に対応します。 _C =0.39×10 ^-9 m ² / s、[24]で報告されたシミュレーションで観察されたように：このモデルはシミュレーション結果を正確に回復することができます（ R ² =0.93）、したがって、式（1）の優れた予測機能を確認します。 （1）新しいシミュレートされた構成の場合も。

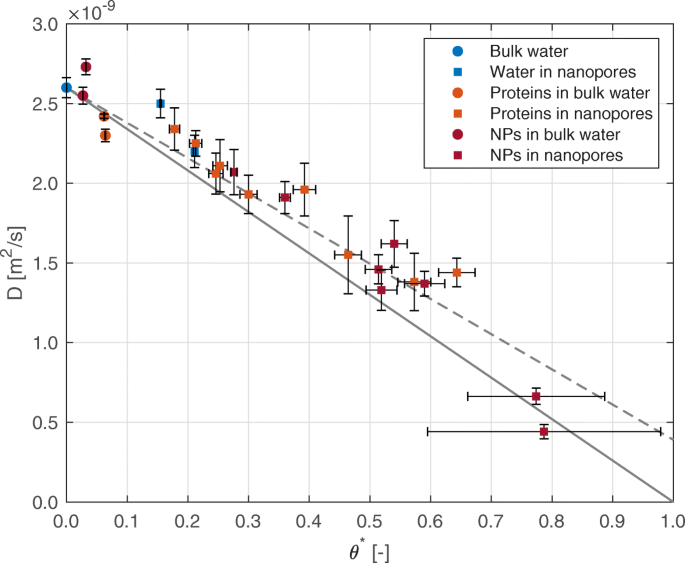
さまざまなシステムの水の自己拡散係数。水の自己拡散係数は、スケーリングパラメータθに対して表示されます。 ^∗ さまざまなシステム用。シリカナノポア内のタンパク質のデータは分子動力学法によって取得されていますが、残りのデータは[24]の補足情報から取得されています。凡例では、ナノ粒子はNPと略されます。 D の値に関する不確実性 平均二乗ゆらぎ（±1s.d。）のフィッティングを参照してください。 θの値の不確実性 ^∗ 水分子にアクセス可能な総体積の推定値（±1s.d。）。実線と破線は、式（1）のモデルを示しています。 （1） D の場合 _C =0および D _C =0.39×10 ^-9 m ² それぞれ/ s

提案されたプロトコルの実際の例

提案されているように、水中の既知の汚染物質の計量装置として使用されるナノポーラスシリカ錠剤を考えてみましょう。懸濁した汚染分子が錠剤に拡散し、平衡に達するように、錠剤を溶液試験サンプルに十分な時間浸したままにしておくと仮定します（これに関する詳細な説明については、次のセクションを参照してください）。次に、サンプルが抽出され、水の自己拡散係数 D 例えば、ＱＥＮＳ測定によって得られた錠剤の多孔質構造の内部。体積分率θ ^∗ 次に、式から簡単に取得できます。 （1）、両方の D _B および D _C 与えられた温度で知られています。次に、重なり合ったナノ閉じ込め量の水をCPTで考慮に入れることができるため、θになります。 =− ln（1− θ ^∗ ）。 1つのナノポアに封入された単一タイプの汚染物質の場合、式（1）は次のようになります。 （2）単純化して

下付き文字である p および P それぞれ粒子と細孔を指します。溶剤アクセス可能領域 SAS 粒子と細孔のナノ閉じ込めの平均特性長\（\ bar {\ delta} \）は分子動力学からわかっており、浮遊粒子の数は

このナノメータリング手順の結果は、タブに報告されています。図1および図3は、図2のシリカナノポア内のタンパク質およびナノ粒子のサンプルケースです。特に、図3の二等分線曲線により、浮遊粒子の推定数の精度を評価できます\（（n_ {p } ^ {e}）\）元の（実際の）1つ\（（n_ {p} ^ {o}）\）に関して、 R ² 0.85に等しい曲線の。

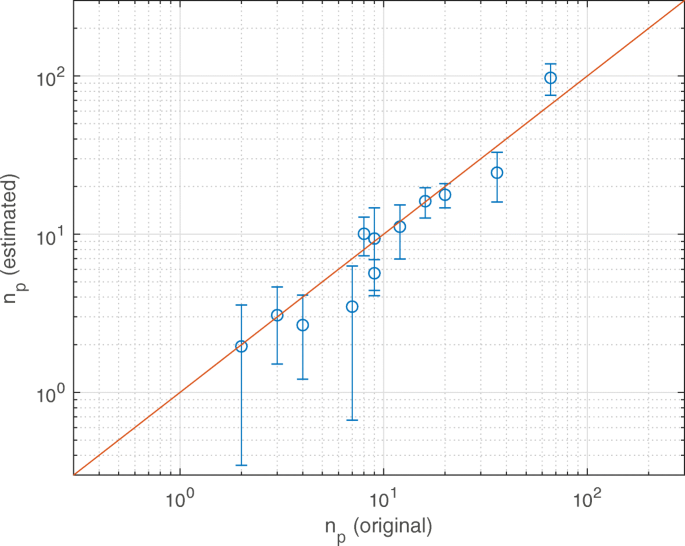
提案されたナノメータリングプロトコルの精度。提案されたプロトコルを使用した推定粒子数と元の粒子数。報告されたデータ（ドット）は、表1の構成を参照しています。実線は二等分線です。 \（n_ {p} ^ {e} \）の値のエラーバーは、 D の変動性から計算されます。 および V _tot 値（不確かさの定量化、±1 s.d。）

ナノポア内の生体分子またはナノ粒子の数を考えると、それらの数濃度は c として簡単に取得できます。 = n _p / V _P 、\（V _ {\ text {P}} =T \ pi d_ {P} ^ {2} / 4 \）である、円筒形のスルー構成の場合の細孔の自由体積[27]（ T は細孔の長さ、つまり、真っ直ぐな細孔の場合のシリカ錠剤の厚さです）。このナノメータリングプロトコルは、ここでは単一の細孔に対して提示されていますが、その多孔性、したがって水和ナノポアの数を考えると、ナノメータリングタブレット全体に簡単に外挿することができます。

ナノポアの充填

前のセクションで説明した例では、平衡状態を説明しているため、ナノポア内の粒子の濃度がバルク溶液の濃度と等しいと仮定しています。それにもかかわらず、この研究で提案されたナノメータリングプロトコルは、検出される溶媒和粒子によるナノポアの充填プロセスも含みます。このセクションでは、ナノポアの特徴的な充填時間に関して、提案されたナノメータリングプロトコルの実際的な実現可能性を評価します。

溶媒和ナノ粒子によるナノポアの充填を最大化するために一般的に使用される実験プロトコルには、超音波処理および遠心分離プロセスが含まれます[43]。 ]。ここでは、最初に乾燥したナノポアへの分散粒子の自発的な溶媒吸収と拡散を検討します。したがって、関連する現象の時間スケールが非常に異なるため、2つの連続するプロセスを考慮して、単純化されたアプローチを採用します。純粋な流体による乾燥細孔の毛細管吸収と、水和細孔を介した平衡状態へのFickianメカニズムによる粒子拡散です。

実験と分子動力学シミュレーション[48–50]は、平均毛細管直径が水の分子直径の約4倍より大きい場合[50、51]、吸収プロセスはLucas-Washburn（LW）方程式で記述できることを示しています。シャープフロント近似では、ダルシーの法則を使用して、移動するフロントの位置をモデル化できます h （ t ）、LW方程式の同じ形式を復元する[52]：

ここで、Δ p 駆動毛細管圧力、μ は流体（この場合は水）の動的粘度です。 ϕ _i は、取り込みプロセスの開始時の媒体の有効気孔率であり、 K その透磁率です。多孔質シリカ材料は、非常に規則的な構造と狭い細孔径分布を示します[46]。したがって、それらの透過性は[49、53]として計算できます。

ここで r ₀ は公称細孔径、 r _h は細孔の水力直径です（ r よりも小さい） ₀ キャピラリー表面に水分子の吸着層があるため）、 ϕ ₀ は媒体の公称気孔率であり、τ その屈曲度です。毛細血管圧は、ヤング・ラプラスの式で表すことができます。

ここで、σ は流体の表面張力であり、 𝜗 細孔表面に対するその動的接触角。シリカ-水界面の場合、 𝜗 ≈0[49、54]。

ナノポーラス錠剤は、直径5〜150 nmの範囲の真っ直ぐな円筒形の細孔と40〜90％の多孔度で正確に製造できます[27]。式6を使用して、このような幾何学的特性（ t ）を持つナノポーラス材料の完全な吸収に必要な時間を見積もることができます。 _i ）、希釈された汚染物質はこのプロセスに影響を与えないという単純化された仮説において。結果の t _i 1 μから変化する錠剤の厚さ（つまり、細孔の長さ）について、青いアスタリスクと点線を使用して図4に報告されています。 mから1mm。結果は、吸収プロセスの驚くべき速度を示しています。考えられる最も厚い巨視的な錠剤は、10秒未満で完全に水で満たされます。分子動力学セットアップによってシミュレートされたものとのコヒーレント構成を分析するために、 t の推定値 _i 最初に乾燥した材料を検討します（つまり、 ϕ ₀ = ϕ _i ）、 d の平均細孔径 ₀ =2 r ₀ =11.04 nm、気孔率と屈曲度は ϕ に等しい ₀ ≈40％ およびτ それぞれ約1。流体力学的半径は、吸着された水分子の影響を考慮に入れる必要があるため、 r _h = r ₀ −2 d _w 、ここで、吸着された水分子の2つの層（ d _w =0.275 nmの直径）が想定されています[24]。細孔内の残りの水は、バルク条件で合理的に考慮することができ、したがって、σ =0.072 N / mおよびμ =10 ⁻³ T でのパス =300K。これらの推定は、吸収プロセスに対する浮遊粒子の影響を無視して実行されます。ただし、粘度や接触角などの水の局所的な特性が変化する可能性があるため、粒子と壁の相互作用は、高体積分率または単位に近い粒子-細孔サイズ比では無視できません[55]。それでも、液体フロントの位置は、式（1）で表すことができます。 （6）粒子-細孔径比が10％以下の場合[55]。

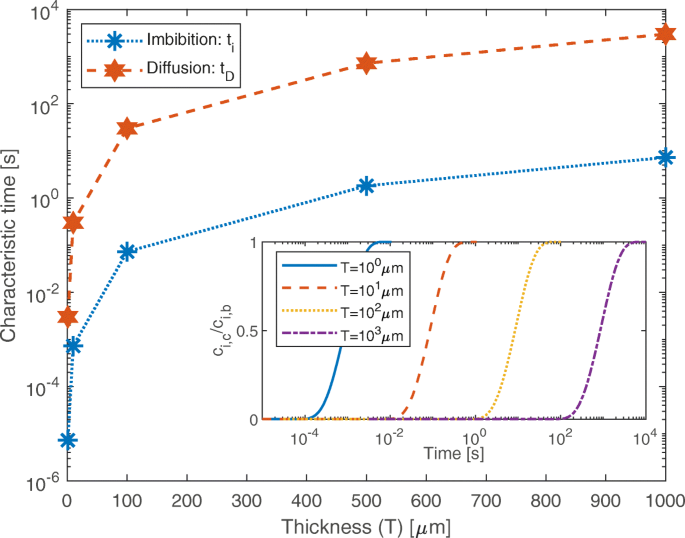
ナノポアの特徴的な充填時間。毛細管現象によるナノポア充填の特徴的な時間（青い点線、 t _i ）および粒子拡散（赤い破線、 t _D ）ナノポーラスシリカ錠剤の厚さを変える（直径11.04 nmのナノポア; 1％重量分率の1AKIタンパク質の水溶液）。完全に水和した細孔を通る粒子拡散プロセスには、特徴的な時間が必要です t _D t より2桁高い _i 、分析されたすべての構成で。挿入図は、ナノポアの中心での粒子濃度の比率を示しています（ c _{i 、 c} 、 x で = T / 2）とバルクのもの（ c _{i 、 b} 、 x で =0および T ）さまざまな厚さ（ T ）の時間の関数として ）錠剤の

次に、完全に水和した均質で真っ直ぐなナノポアへの粒子の拡散に必要な特徴的な時間を評価します。この充填プロセスは、純粋な拡散に依存していると想定されており[56、57]、粒子と細孔の相互作用が無視できると仮定すると、フィックの方程式で表すことができます。

c であること _i 粒子濃度、 D _e = ϕ ₀ D _p / τ 水和チャネル内の粒子の有効拡散係数、および D _p バルク流体におけるそれらの拡散係数。

最初の例として、 c で希釈されたリゾチーム（1AKI）溶液を考慮して計算が実行されます。 _{i 、 b} =3.4 mol / m ³ 濃度、すなわち、約1％の重量分率。 t を推定するために採用された構成と同様 _i 、平均細孔径が d のシリカ錠 ₀ =2 r ₀ =11.04 nm、さまざまな厚さ、 ϕ に等しい気孔率 ₀ ≈40％ 、および屈曲度τ ≈1が考慮されます。粒子が内部にない完全に水和した細孔から開始して、充填時間 t _D c に到達するのに必要な時間として推定されます _{i 、 c} =0.95 c _{i 、 b} 毛穴の中心、つまり x = T / 2。粒子濃度は一定で、 c に等しくなります _{i 、 b} チャネルの両端、つまり x =0および T 。水中でのリゾチームの拡散係数は、バルク値、つまり D に等しいと想定されます。 _p =11.08・10 ⁻¹¹ m ² / s [58、59]。式9は、有限要素法によって1次元で数値的に解かれます。結果は図4に赤い星と破線で報告されており、 t であることを示しています。 _D t よりも約2桁高い _i シリカ錠剤の所定の厚さに対して。提示された最悪の場合でも（ T =1 mm、 t _D 約3000秒）、充填時間は実際に関心のあるナノメータリングプロトコルと互換性があるようです。文献のシミュレーション[60]と実験[61]の両方が、粒子の拡散係数 D を示していることに注意してください。 _p 粒子の細孔表面との親和性が異なり、移動度の低いナノ閉じ込め水が存在するため、ナノ細孔内の粒子はバルク粒子よりも大幅に低くなる可能性があります。したがって、提案されたアプローチは、特徴的な充填時間に関する最初の指標を提供しますが、より正確な推定を達成するために、 D _p したがって、 t _D ケースバイケースで分析する必要があります[62]。

2番目の例として、溶媒和薬物の濃度を測定する可能性を評価します。これは、溶媒和薬物が現在、水源の新たな汚染物質と見なされているためです[5]。特に、癌治療に関連する薬剤の1つであるドキソルビシンを分析します。ドキソルビシンは化学療法に一般的に使用される疎水性分子です[63–65]。拡散時間の推定 t _D 水和シリカナノタブレットへのドキソルビシンの注入は、前のケーススタディですでに採用されている仮定の下で実行できます。非結合ドキソルビシンの拡散係数は D _p =1.6・10 ^-10 m ² / s [66];したがって、500 μのシリカタブレット mの厚さは、バルク濃度の95％で充填されます（ c _{i 、 b} =3.4 mol / m ³ ）約500秒で。この実例となる事例は、提案されたナノメータリングプロトコルが水中の薬物痕跡の濃度を検出するためにも潜在的に使用できることを示しています。この簡略化されたモデルでは考慮されていない追加の要因（たとえば、薬物と細孔表面間の化学親和力、pH、界面活性剤の存在または官能化）の影響は、特性時間を大幅に逸脱する可能性があるため、実験的に調査する必要があることに注意してください。考慮される単純化された条件に関して。

明らかに、ナノポアの充填時間は t の間にあるはずです。 _i （最良の場合、ナノ粒子は毛細管現象によって水と一緒に細孔に引きずり込まれます）および t _D （最悪の場合、水は最初に細孔を水和し、次にナノ粒子はフィキアン拡散が続きます）。最悪の調査の場合でさえ、ナノポアの充填時間のモデリング推定は、提案されたナノメータリングプロトコルの実際的な実現可能性を示しています。この考えは、文献のいくつかの有望な実験的証拠によっても裏付けられています。たとえば、平均直径300 nmの親水性カーボンナノチューブは、10〜50 nmの範囲の粒子を自発的に吸収することで簡単に満たされ[67、68]、構成の幾何学的および化学的パラメーターを適切に調整することで、ナノチャネルの高速で均一な充填により、提案されたナノメータリングプロトコルが実現可能になります。

仮説の意味

珪藻藻類フラスチュールの規則的なナノポーラス構造に触発されて、この作業では、水に分散したナノ粒子または生体分子の濃度を測定するための新しい概念を提示しました。藻類のフラスチュールの規則的な構造は、ナノポーラスシリカ錠剤によって人工的に再現できます。その細孔サイズ、厚さ、および形状は、粒子の選択的取り込みを最適化するために正確に調整する必要があります。提案されているナノメータリング方法は、タブレットの細孔内にナノ閉じ込められた水の自己拡散係数に対するこれらのナノ粒子または生体分子の影響に依存しており、次の手順で構成されています。

1. 1。

   ナノポアのサイズ分布が制御された多孔質タブレットを合成します。

2. 2。

   タブレットのナノポアに、毛細管吸収と粒子拡散によって検出される粒子を含む溶液を充填させ、ナノポアと周囲の溶液との間の平衡状態を実現します。

3. 3。

   タブレットを溶液から取り出し、QENSまたはD-MRI技術などによって、粒子で満たされた水和ナノポア内の水の自己拡散係数を測定します。

4. 4。

   測定された水の自己拡散係数を、式（1）を使用して粒子濃度と相関させます。 1から（5）。ナノポアと粒子の溶媒接触可能な表面（ SAS ）およびナノ閉じ込めの平均特性長（\（\ bar {\ delta} \））は、分子動力学から計算するか、利用可能なデータベースから取得する必要があります。

提案されたナノメータリングプロトコルの実現可能性を評価するために、分子動力学シミュレーションと文献からの証拠が採用されています。さまざまな濃度の酸化鉄ナノ粒子またはタンパク質で満たされた水和ナノポアが分析され、ナノ閉じ込め水の計算された自己拡散係数と予測された自己拡散係数の一致が見出され、粒子濃度を推定できるようになりました。ナノポアの充填に関与するメカニズムの予備分析も実施されました。時間スケールが異なるため、2つの異なる現象が別々に考慮されています。毛細管現象によって駆動される純水による乾燥錠剤の吸収と、濃度勾配によって駆動される水和細孔を介した粒子拡散です。結果は、充填プロセスの主要な特徴的な時間は、粒子が水和した細孔に拡散するのに必要な時間であることを示しています。ただし、考慮される最も厚い錠剤（1 mm）の場合でも、推定充填時間は1時間を超えないため、ナノメータリングプロトコルの実用的な実現可能性を損なうことはありません。

提案されたナノメータリング法は、数値の観点から有望な結果を示していますが、実際の実験の実装は、いくつかの追加の問題に直面する必要があるかもしれません。第一に、細孔表面と粒子の間の相互作用は無視できない可能性があり、したがって充填プロセスを変える可能性があります（例えば、細孔の詰まり）。この効果により、バルク溶液中の粒子の実際の濃度と細孔内で測定された粒子の濃度との間にバイアスが生じる可能性があります。このような問題は、検出される粒子と相互作用してはならない細孔の表面特性を正確に選択することで解決できます。第二に、現在の実験手法では、単一ナノポアの分解能で水の拡散係数を測定するのが難しい可能性があります。この問題は、数百または数千のナノポアにわたる平均自己拡散係数を測定することで軽減できます。これにより、錠剤全体に不均一な粒子が充填された場合に、より優れた統計的サンプリングが可能になります。第三に、ナノメータリングプロトコルの不確実性は実験によって評価されるべきです。分子動力学によって研究された構成は、最大±50 ％の予測誤差を明らかにしました ：この誤差範囲は、時間（複数の測定値）と空間（数百または数千の細孔の平均）の両方の観点から、より大きな統計サンプルを考慮することによって最終的に減らすことができます。第四に、ナノポアの最適な直径は、検出される粒子の予想されるサイズと濃度に基づいて決定する必要があります。一方では、細孔径はθが低くならないように選択する必要があります。 ^∗ （例：θ ^∗ これは、水の自己拡散係数のごくわずかな変動につながる可能性があり、最終的にはQENSまたはD-MRI技術の分解能を下回る可能性があるため、> 0.2）である必要があります。一方、高レベルの水のナノ閉じ込めも避ける必要があります（例：θ ^∗ 細孔の詰まりや粒子の凝集/分離のリスクを制限し、濃度の結果に偏りを生じさせるために、<0.8）にする必要があります。

結論として、この研究で議論された元のナノメータリングプロトコルを実験的に検証するには、さらなる研究が必要です。しかし、提示された数値結果は、このアイデアの可能性を証明しており、水または生体分子中の新たなナノ汚染物質の完全に新しいクラスの検出プロセスへの道を開く可能性があります。視点から見ると、ナノポーラスシリカタブレットなどの計量デバイスの微視的なサイズにより、ラボオンチップデバイスによるナノ計量プロセスの自動化が可能になる場合があります。

データと資料の可用性

現在の研究中に使用および/または分析されたデータセットは、合理的な要求に応じて対応する著者から入手できます。

略語

1AKI：

リゾチーム

1UBQ：

ユビキチン

CPT：

連続体パーコレーション理論

D-MRI：

拡散磁気共鳴画像法

IONP：

酸化鉄ナノ粒子

LINCS：

線形制約ソルバー

LW：

ルーカス-ウォッシュバーン

MD：

分子動力学

MOL：

分子

MRI：

磁気共鳴画像法

NP：

ナノ粒子

PME：

パーティクルメッシュエヴァルト

QENS：

準弾性中性子散乱

SAS：

溶媒接触表面積