Python実装のためのニューラルネットワークアーキテクチャ
この記事では、ニューラルネットワークのトレーニングと分類の実験に使用するパーセプトロン構成について説明し、関連トピックについても説明します。バイアスノードの数。
All AboutCircuitsニューラルネットワークシリーズの技術記事へようこそ。これまでのシリーズ(以下にリンク)では、ニューラルネットワークを取り巻く理論のかなりの部分を取り上げました。
- ニューラルネットワークを使用して分類を実行する方法:パーセプトロンとは何ですか?
- 単純なパーセプトロンニューラルネットワークの例を使用してデータを分類する方法
- 基本的なパーセプトロンニューラルネットワークをトレーニングする方法
- 単純なニューラルネットワークトレーニングを理解する
- ニューラルネットワークのトレーニング理論の概要
- ニューラルネットワークの学習率を理解する
- 多層パーセプトロンを使用した高度な機械学習
- シグモイド活性化関数:多層パーセプトロンニューラルネットワークでの活性化
- 多層パーセプトロンニューラルネットワークをトレーニングする方法
- 多層パーセプトロンのトレーニング式とバックプロパゲーションを理解する
- Python実装のためのニューラルネットワークアーキテクチャ
- Pythonで多層パーセプトロンニューラルネットワークを作成する方法
- ニューラルネットワークを使用した信号処理:ニューラルネットワーク設計での検証
- ニューラルネットワークのデータセットのトレーニング:Pythonニューラルネットワークをトレーニングおよび検証する方法
これで、この理論的知識を機能的なパーセプトロン分類システムに変換する準備が整いました。
まず、高級プログラミング言語で実装するネットワークの一般的な特徴を紹介します。私はPythonを使用していますが、コードはCなどの他の言語への翻訳を容易にする方法で記述されます。次の記事ではPythonコードの詳細なウォークスルーを提供し、その後、さまざまなトレーニング方法を検討します。 、このネットワークの使用と評価。
Pythonニューラルネットワークアーキテクチャ
このソフトウェアは、次の図に示されているパーセプトロンに対応しています。
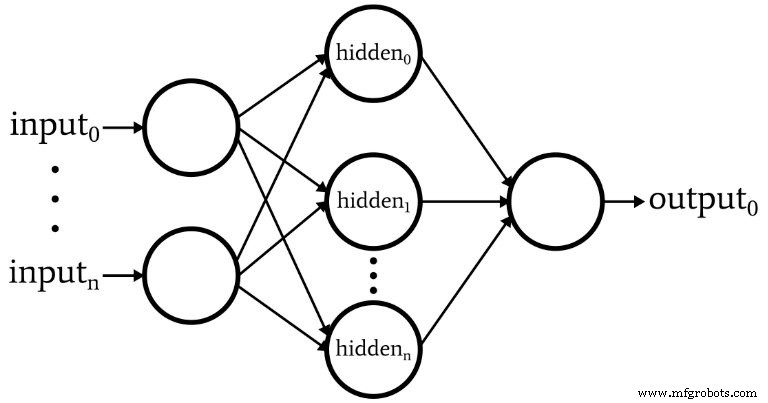
ネットワークの基本的な特徴は次のとおりです。
- 入力ノードの数は可変です。入力の次元は分類するサンプルの次元と一致する必要があるため、これは、かなりの柔軟性を備えたネットワークが必要な場合に不可欠です。
- コードは複数の非表示レイヤーをサポートしていません。この時点では必要ありません。非常に強力な分類には、1つの隠れ層で十分です。
- 1つの隠れ層内のノードの数は可変です。最適な数の非表示ノードを見つけるには、試行錯誤が必要ですが、妥当な開始点を選択するのに役立つガイドラインがあります。隠れ層の次元の問題については、今後の記事で説明します。
- 現在、出力ノードの数は1つに固定されています。この制限により、最初のプログラムが少し簡単になり、可変出力の次元を改善されたバージョンに組み込むことができます。
- 非表示ノードと出力ノードの両方の活性化関数は、標準のロジスティックシグモイド関係になります。
\ [f(x)=\ frac {1} {1 + e ^ {-x}} \]
バイアスノードとは何ですか? (パーセプトロンの場合、別名バイアスは良いです)
ネットワークアーキテクチャについて説明している間、ニューラルネットワークにはバイアスノードと呼ばれるものが組み込まれていることが多いことを指摘しておく必要があります(または、「ノード」なしで単に「バイアス」と呼ぶこともできます)。バイアスノードに関連付けられた数値は、設計者が選択した定数です。例:
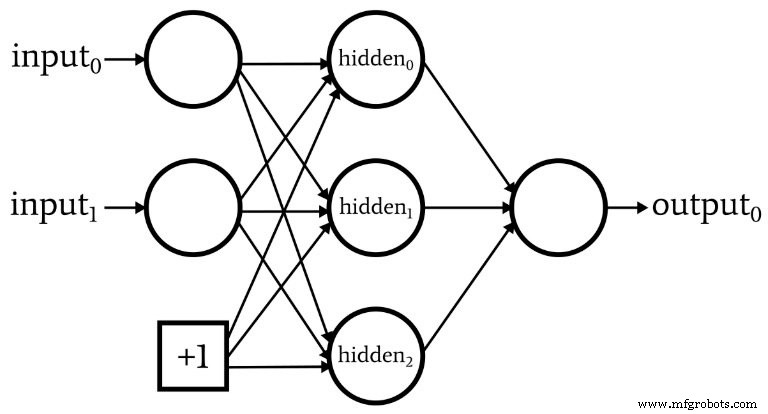
バイアスノードは、入力レイヤーまたは非表示レイヤー、あるいはその両方に組み込むことができます。それらの重みは他の重みと同様であり、同じバックプロパゲーション手順を使用して更新されます。
バイアスノードの使用は、入力ノードまたは非表示ノードの数を簡単に変更できるニューラルネットワークコードを作成する重要な理由です。1つの特定の分類タスク、可変入力層および非表示層の次元のみに関心がある場合でも、バイアスノードを使用して便利に実験できるようにします。
パート10では、ノードの事前アクティブ化信号は内積を実行することによって計算されることを指摘しました。つまり、2つの配列(または必要に応じてベクトル)の対応する要素を乗算してから、個々の積をすべて合計します。最初の配列は前のレイヤーからのアクティブ化後の値を保持し、2番目の配列は前のレイヤーを現在のレイヤーに接続する重みを保持します。したがって、前層のアクティブ化後の配列がxで示され、重みベクトルがwで示される場合、アクティブ化前の値は次のように計算されます。
\ [S_ {preA} =w \ cdot x =sum(w_1x_1 + w_2x_2 + \ cdots + w_nx_n)\]
これがバイアスノードと一体何の関係があるのか疑問に思われるかもしれません。バイアス(bで示される)は、この手順を次のように変更します。
\ [S_ {preA} =(w \ cdot x)+ b =sum(w_1x_1 + w_2x_2 + \ cdots + w_nx_n)+ b \]
バイアスは、活性化関数によって処理される信号をシフトし、それによってネットワークをより柔軟で堅牢にすることができます。バイアス値を示すために文字bを使用することは、直線の標準方程式の「y切片」を連想させます。y=mx + b 。そして、これは偶然の一致ではありません。バイアスは確かにy切片のようなものであり、重みの配列が勾配と同等であることに気付いたかもしれません。
\ [S_ {preA} =(w \ cdot x)+ b \]
\ [y =mx + b \]
ウェイト、バイアス、アクティベーション
トレーニング中にノードの活性化関数に提供される数値を考えると、重みは入力データの傾きを増減し、バイアスは入力データを垂直方向にシフトします。しかし、これはノードの出力にどのように影響しますか?さて、アクティベーションに標準のロジスティック関数を使用していると仮定しましょう:
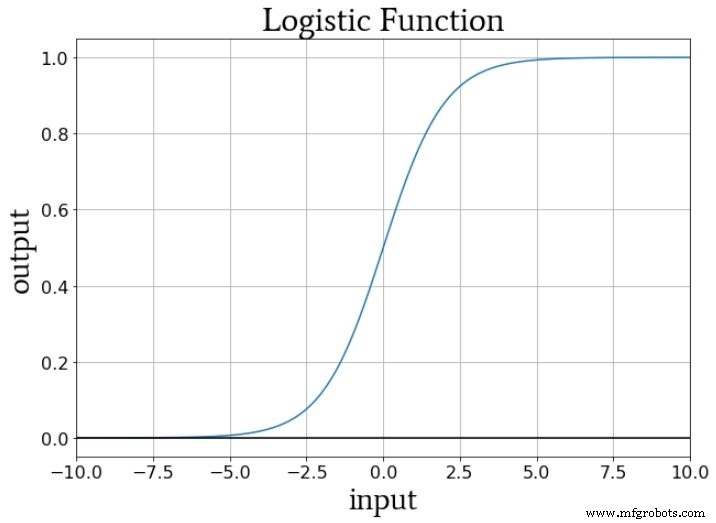
f A からの移行 (x)=0からf A (x)=1はx =0の入力値を中心とします。したがって、バイアスを使用して事前アクティブ化信号を増減することにより、遷移の発生に影響を与え、アクティブ化関数を左または右にシフトできます。 。一方、重みは、入力値がx =0を「すばやく」通過する方法を決定します。これは、活性化関数の遷移の急峻さに影響します。
結論
バイアスノードと、ソフトウェアに実装する最初のニューラルネットワークの顕著な特徴について説明しました。これで実際のコードを確認する準備が整いました。これが次の記事で行うことです。
産業用ロボット



