多層パーセプトロンのトレーニング式とバックプロパゲーションを理解する

この記事では、重み更新の計算を実行するときに使用する方程式を示し、バックプロパゲーションの概念についても説明します。

機械学習に関するAACのシリーズへようこそ。

ここまでのシリーズに追いつく：

1. ニューラルネットワークを使用して分類を実行する方法：パーセプトロンとは何ですか？
2. 単純なパーセプトロンニューラルネットワークの例を使用してデータを分類する方法
3. 基本的なパーセプトロンニューラルネットワークをトレーニングする方法
4. 単純なニューラルネットワークトレーニングを理解する
5. ニューラルネットワークのトレーニング理論の概要
6. ニューラルネットワークの学習率を理解する
7. 多層パーセプトロンを使用した高度な機械学習
8. シグモイド活性化関数：多層パーセプトロンニューラルネットワークでの活性化
9. 多層パーセプトロンニューラルネットワークをトレーニングする方法
10. 多層パーセプトロンのトレーニング式とバックプロパゲーションを理解する
11. Python実装のためのニューラルネットワークアーキテクチャ
12. Pythonで多層パーセプトロンニューラルネットワークを作成する方法
13. ニューラルネットワークを使用した信号処理：ニューラルネットワーク設計での検証
14. ニューラルネットワークのデータセットのトレーニング：Pythonニューラルネットワークをトレーニングおよび検証する方法

ニューラルネットワーク理論の基本的なトピックを慎重に検討する必要がある段階に到達しました。多層パーセプトロン（MLP）の重みを微調整して、入力サンプルを正確に分類できるようにする計算手順です。これにより、ニューラルネットワーク設計の重要な側面である「バックプロパゲーション」の概念が導き出されます。

ウェイトの更新

MLPのトレーニングに関する情報は複雑です。さらに悪いことに、オンラインリソースではさまざまな用語や記号が使用されており、さまざまな結果が得られるようです。ただし、結果が本当に異なるのか、同じ情報を異なる方法で提示しているだけなのかはわかりません。

この記事に含まれている方程式は、このブログ投稿でDustinStansbury博士によって提供された派生と説明に基づいています。彼の治療法は私が見つけた中で最高のものであり、最急降下法とバックプロパゲーションの数学的および概念的な詳細を掘り下げたい場合は、ここから始めるのが最適です。

次の図は、ソフトウェアに実装するアーキテクチャを表しています。以下の式は、このアーキテクチャに対応しています。これについては、次の記事で詳しく説明します。

用語

明確な用語を維持しないと、このトピックはすぐに管理できなくなります。次の用語を使用します：

• 事前アクティベーション （省略形 \（S_ {preA} \） ）：これは、ノードの活性化関数への入力として機能する信号（実際には1回のトレーニング反復のコンテキスト内の単なる数値）を指します。 ドット積を実行して計算されます 重みを含む配列と、前の層のノードから発生した値を含む配列の例。内積は、2つの配列の要素ごとの乗算を実行し、その乗算の結果として配列内の要素を合計することと同じです。
• アクティベーション後 （省略形 \（S_ {postA} \） ）：これは、ノードを出る信号（ここでも、個々の反復のコンテキスト内の数値）を指します。これは、活性化機能を事前活性化信号に適用することによって生成されます。 \（f_ {A}（）\）で表される活性化関数の私の好みの用語 、ロジスティック シグモイドではなく。
• Pythonコードでは、 ItoH でラベル付けされた重み行列が表示されます。 および HtoO 。これらの識別子を使用するのは、「隠れ層の重み」のようなものを言うのが曖昧だからです。これらは、前に適用される重みでしょうか。 隠しレイヤーまたは後 隠された層？私のスキームでは、ItoHは入力ノードから非表示ノードに転送される値に適用される重みを指定し、HtoOは非表示ノードから出力ノードに転送される値に適用される重みを指定します。
• トレーニングサンプルの正しい出力値は、ターゲットと呼ばれます。 T で表されます 。
• 学習率 LR と略されます 。
• 最終エラー 出力ノードからのアクティブ化後の信号の差です（ \（S_ {postA、O} \） ）およびターゲット。 \（FE =S_ {postA、O} --T \）として計算されます。 。
• エラー信号 （ \（S_ {ERROR} \） ）は、出力ノードの活性化関数を介して隠れ層に向かって伝播される最終エラーです。
• グラデーション エラー信号への特定の重みの寄与を表します。この寄与を差し引くことによって重みを変更します（必要に応じて学習率を掛けます）。

次の図は、ネットワークの視覚化された構成内にこれらの用語の一部を示しています。私は知っています—それは色とりどりの混乱のように見えます。謝罪します。これは情報が密集した図であり、一見少し不快かもしれませんが、注意深く研究すれば非常に役立つと思います。

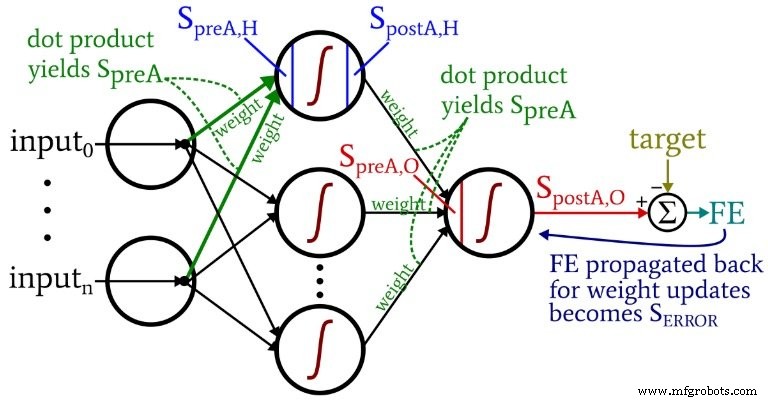
重み更新方程式は、変更する重みに関して、誤差関数の偏導関数（合計二乗誤差を使用しています。活性化関数を扱うシリーズのパート8を参照）を使用して導出されます。数学を見たい場合は、スタンズベリー博士の投稿を参照してください。この記事では、結果に直接スキップします。非表示から出力への重みについては、次のものがあります。

\ [S_ {ERROR} =FE \ times {f_A} '（S_ {preA、O}）\]

\ [gradient_ {HtoO} =S_ {ERROR} \ times S_ {postA、H} \]

\ [weight_ {HtoO} =weight_ {HtoO}-（LR \ timesgradient_ {HtoO}）\]

エラー信号を計算します l 最終エラーを乗算します 導関数を適用したときに生成される値によって 活性化関数の 事前アクティベーションシグナルへ 出力ノードに配信されます（\（{f_A} '（S_ {preA、O}）\）の1次導関数を示すプライム記号に注意してください）。 グラデーション 次に、エラー信号を乗算して計算されます。 アクティベーション後のシグナルによる 隠された層から。最後に、このグラデーションを差し引いて重みを更新します 現在の重み値から、勾配を掛けることができます 学習率による ステップサイズを変更したい場合。

入力から非表示への重みについては、次のようになります。

\ [gradient_ {ItoH} =FE \ times {f_A} '（S_ {preA、O}）\ times weight_ {HtoO} \ times {f_A}'（S_ {preA 、H}）\ times input \]

\ [\ Rightarrowgradient_ {ItoH} =S_ {ERROR} \ times weight_ {HtoO} \ times {f_A} '（S_ {preA、H}）\ times input \]

\ [weight_ {ItoH} =weight_ {ItoH}-（LR \ timesgradient_ {ItoH}）\]

入力から非表示への重みを使用すると、エラーを追加のレイヤーに伝播して戻す必要があります。これを行うには、エラー信号を乗算します。 出力に隠された重みによる 対象の隠れノードに接続されています。したがって、入力から非表示への重みを更新する場合 これが最初の隠れノードにつながり、エラー信号を乗算します。 最初の隠れノードを出力ノードに接続する重みによって。次に、非表示から出力への重みの更新と同様の乗算を実行して計算を完了します。 導関数を適用します。 活性化関数の 隠れノードの事前アクティベーション信号へ 、および「入力」値は、アクティブ化後の信号と考えることができます。 入力ノードから。

バックプロパゲーション

上記の説明は、バックプロパゲーションの概念にすでに触れています。この概念を簡単に補強し、ニューラルネットワークの議論で頻繁に現れるこの用語に明確に精通していることを確認したいと思います。

バックプロパゲーションにより、パート8で説明した隠れノードのジレンマを克服できます。ネットワークで生成された出力とトレーニングデータによって提供されたターゲット出力値の差に基づいて、入力から非表示への重みを更新する必要がありますが、これらの重みは影響します。生成された出力は間接的に。

バックプロパゲーションとは、エラー信号を1つ以上の隠れ層に送り返し、隠れノードから発生する重みと隠れノードの活性化関数の導関数の両方を使用してそのエラー信号をスケーリングする手法を指します。全体的な手順は、出力エラーへの重みの寄与に基づいて重みを更新する方法として機能します。ただし、その寄与は、入力から非表示への重みと生成された出力値の間の間接的な関係によって不明瞭になります。

結論

多くの重要な資料を取り上げました。この記事には、ニューラルネットワークのトレーニングに関する非常に貴重な情報があると思います。ご同意いただければ幸いです。シリーズはさらにエキサイティングになり始めるので、新しい記事をチェックしてください。