eの電力関数の導関数
eの導関数の例
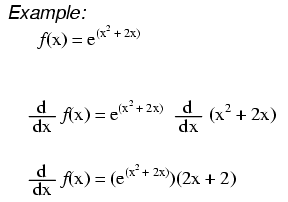
比例定数
関係や現象が「指数関数的」であると言うとき、電流、利益、人口などの量は、量が増えるにつれてより急速に増加することを意味します。言い換えると、特定の変数に関する変化率は、その変数の値に比例します。これは、指数関数の導関数が、元の指数関数に定数( k )を掛けたものに等しいことを意味します。 )比例関係を確立します。
$$ \ frac {\ text {d}} {\ text {d} x} a ^ x =ka ^ x $$
比例定数は、指数の底の自然対数に等しくなります:
$$ \ frac {\ text {d}} {\ text {d} x} a ^ x =\ ln(a)\ times a ^ x $$
したがって、底の自然対数が1に等しい場合、関数の導関数は元の関数に等しくなります。これはまさにeのべき乗関数で起こることです。eの自然対数は1であり、その結果、$$ e ^ x $$の導関数は$$ e ^ x $$です。
$$ \ frac {\ text {d}} {\ text {d} x} e ^ x =e ^ x $$
「連鎖」ルール
指数式が単純なx以外の場合は、連鎖律を適用します。最初に式全体の導関数を取得し、次に指数の式の導関数を乗算します。
$$ \ frac {\ text {d}} {\ text {d} x} e ^ {x ^ 2 + 2x} =e ^ {x ^ 2 + 2x} \ times \ frac {\ text {d}} { \ text {d} x}(x ^ 2 + 2x)=(2x + 2)e ^ {x ^ 2 + 2x} $$
この手法は、ダイオード電圧に対するダイオード電流の変化率を見つけるために使用できます。次の式は、ダイオード両端の電圧($$ V_D $$)とダイオードを流れる電流($$ I_D $$)の間のおおよその関係を示しています。
$$ I_D =I_S \ times e ^ \ frac {V_D} {0.026} $$
(ダイオードの電流-電圧方程式の詳細については、ダイオードと整流器のページを参照してください。また、$$ I_S $$は定数であり、変数ではないことに注意してください。)電圧に対する電流の変化率を見つけるには、派生物を取ります:
$$ \ frac {\ text {d} I_D} {\ text {d} V_D} =\ frac {\ text {d}} {\ text {d} V_D}(I_S \ times e ^ \ frac {V_D} { 0.026})=I_S \ times e ^ \ frac {V_D} {0.026} \ times \ frac {1} {0.026} $$
したがって、ダイオード電圧$$ V_D $$の特定の値で、電圧の増分増加は、$$ \ frac {I_S} {0.026} e ^ \ frac {V_D} {0.026} $$に等しい電流の増加を作成します。 。
関連するワークシート:
-
電気回路ワークシートの微積分
産業技術



