ナノスケール脂肪フラクタルからの小角散乱

はじめに

ナノスケールおよびマイクロスケールで生成された多くの階層構造は、スケール拡張下で不変であり、自己相似性を示し、したがってフラクタル特性を有する幾何学的特性を持っています[1、2]。材料科学とナノテクノロジーの最近の進歩により、正確な自己相似性を備えたさまざまな人工ナノ/マイクロスケールの決定論的フラクタルの作成が可能になりますが[3–7]、自然過程の大部分はランダムで統計的に自己相似なフラクタルを生成します。自然なフラクタル形成の構造研究における良い近似は、ランダムなものと同じフラクタル次元で、決定論的なフラクタルモデルに頼って行うことができます。このアプローチは、ランダムなフラクタル表面を横切る転送が決定論的モデルジオメトリの応答に非常に近いことを示すためにうまく使用されました[8]。決定論的フラクタルの構築アルゴリズムに多分散度を導入することにより、ランダムフラクタルに対応するものと同様の小角散乱（SAS）強度を得ることができます[9]。さらに、「決定論的」アプローチは計算効率が高く、フラクタル形式、構造因子、回転半径などのさまざまなプロパティの分析的記述が可能になります。

決定論的フラクタルとランダムフラクタルの両方の構造特性を決定するための最も信頼できる方法の1つ[10、11]は、中性子または電磁波（x -光線、光など）[12]。このため、この研究分野での実験的決定に関連する理論的記述の基本的なタスクの1つは、フラクタルの構造とそれに対応する回折スペクトルまたは散乱強度分布と散乱波数ベクトルの関係を明らかにすることです。多くの実験的および理論的研究がこの方向で実施されました[13–21]。

標準的な理論計算と補間を使用して、これらの種類の実験測定から決定されるパラメーターは、質量フラクタル次元 D です。 _m （付録1を参照）、 D _m D _s 、 d -1 < D _s < d 。 d で表しました フラクタルが埋め込まれているユークリッド次元。質量フラクタル次元は、質量 M の方法を表します。 （ r ）半径 r のディスクに埋め込まれると変化します 。得られた質量半径 関係\（M（r）\ p​​ropto r ^ {D _ {\ mathrm {m}}} \）は、散乱強度\（I（q）\ propto q ^ {-D _ {\ mathrm {m} }} \）。明らかに、 D _m 散乱波数ベクトル q の関数としての散乱強度のべき乗則依存性の指数で識別できます。 [18、22]。 D の値が高いほど _m 、よりコンパクトな構造です。同様に、表面フラクタルの場合、その表面分布は\（S（r）\ p​​ropto r ^ {2-D _ {\ mathrm {s}}} \）に従い、したがって\（\ phantom {\ dot { i} \！} I（q）\ propto q ^ {-（2 \ mathrm {d} -D _ {\ mathrm {s}}）} \）[19、23]。 3次元ユークリッド空間での作業 D _s 表面がほぼ完全に滑らかになると、最小値の2に近づきます。折りたたんでほぼ完全にスペースを埋める場合は、最大3つになる傾向があります。

さまざまな化学合成および生物学的システムからの多くの実験的回折強度は、一定の強度の領域によってインターリーブされたべき乗則の減衰の連続によって、二重対数スケールで特徴付けられます。この挙動は、一部のポリマーゲル[24]、セロビオース基質のグリコシドヒドロラーゼ[25]、高分子電解質複合コアセルベート[26]、またはナノポーラスカーボン[27]で確認できます。従来のBeaucageモデル[28]は、これらのシステムに関する基本的な構造情報（つまり、質量または表面のフラクタル次元と各構造レベルの全体的なサイズ）を提供できますが、対応する構成の数が多いため、より完全な特性評価が必要です。フラクタル次元の固定値。この問題は最近、Cherny etalによって部分的に対処されました。 [29]小角散乱（SAS）モデルのコンテキストで。単一スケールの決定論的質量フラクタルの場合、フラクタル反復数、基本構成単位の数、スケーリング係数などの追加情報を取得できることが示されました。このアプローチは、べき乗則の崩壊の連続が散乱分布に存在する場合、脂肪フラクタルの新しいモデルを開発するためにさらにうまく使用されました。これは、基本コンポーネントユニットの全体的なサイズがそれらの間の距離と同じオーダーである構造に適用できます[30、31]。

この記事で紹介する理論モデルは、以前のモデルを組み合わせて適用範囲を拡張します。散乱指数の値が任意に減少するおよびを使用して、べき乗則の減衰の連続を記述します。 一定の強度の領域によってインターリーブされます。私たちのモデルは、ナノ/マイクロフラクタルの各構造レベルに関するより詳細な情報を提供することもできます。この目的のために、反復数に依存するスケーリング係数を持つ2次元の決定論的質量フラクタルで表される脂肪フラクタルを検討しますが、表面積が消失しないため、反復回数が多いため、正の値になります。ルベーグ測度。フラクタル形式と構造因子の分析式を導き出し、各構造レベルでフラクタル次元とスケーリング因子を決定する方法を示します。

理論的背景

ここでΣで示される、同様に配向された同一の回折アパーチャのアレイを検討します。 、 N を含む j でラベル付けされた透明な領域 、各アパーチャから得られた振幅の合計を考慮に入れる必要があります。したがって、単一アパーチャの回折振幅のよく知られた度数分布（付録2の式（37））は、[32]と書き直すことができます。

j のローカルフレーム内の点の座標 絞りは（ x _j 、 y _j ）、および T （ x、y ）は、各透明領域に対応する個々の透過関数を表します。私たちの場合、アパーチャは同じ個別の分布関数で記述されているため、合計と積分を交換できます。 （1）次のように書き直すことができます：

前の等式からの積分係数は、上記のように、同一のアパーチャのそれぞれの分布関数のフーリエ変換を表します。この振幅は、合計を含む係数によって変調され、\（A _ {\ delta}〜=〜\ sum _ {j〜 =〜1} ^ {N}（x〜）の形式のディラックのデルタ分布のフーリエ変換を表します。 -〜x_ {j}）（y〜-〜y_ {j}）\）。したがって、アレイ内のアパーチャの空間分布も考慮されます。したがって、式。 （2）配列定理[32]として知られる形式で書き直すことができます：

フーリエ面での回折像の強度分布は次のようになります。

予想通り、積の最初の要素は単一の穴の散乱強度に対応し、2番目の要素はこれらの穴が回折開口内に分布する方法を明らかにしますΣ 。これらの量は、フォームファクター F とも呼ばれます。 （ p、q ）およびそれぞれ、構造因子 S （ p、q ）。そのため、論文全体で得られた結果は、次の形式の散乱強度を使用して表されます。

ファットフラクタルモデルとメソッド

薄い（通常の）Cantorフラクタルを構築するための詳細な手順はよく知られています[33]。ここでは、主要な建設手順のみを要約します。上から下へのアプローチが採用されています。エッジ l の最初の正方形（または他のユークリッド形状）から開始します ₀ （ m =0）、その中心がデカルト座標系の原点と一致し、エッジが座標系の軸に平行である場合、正方形内の任意の点が条件- l を満たします。 ₀ /2≤ x ≤ l ₀ / 2および- l ₀ /2≤ y ≤ l ₀ / 2。最初の反復時（ m =1）、正方形は他の4つの正方形に分割され、辺の長さは\（\ beta _ {\ mathrm {s}} ^ {（1）} l_ {0} \）です。 \（\ beta _ {\ mathrm {s}} ^ {（1）} \ equiv（1- \ gamma _ {1}）/ 2 \）、\（0 <\ beta _ {\ mathrm { s}} ^ {（1）} <1/2 \）、最初の反復スケーリング係数、およびγ ₁ m の場合の図1a、b）に見られるように、この時点で除去された長さの割合。 =1.（⋯）の間に配置された数値は、上位インデックスとして表示され、反復回数を数値化します。べき関数の指数として解釈してはなりません。スケーリング係数に関して、4つの正方形の位置はベクトル\（\ boldsymbol {a} _ {j}〜=〜\ left \ {\ pm \ beta _ {\ mathrm {t}} ^ { （1）} l_ {0}、\ pm \ beta _ {\ mathrm {t}} ^ {（1）} l_ {0} \ right \} \）すべての可能な符号の組み合わせ。ここで\（\ beta _ { \ mathrm {t}} ^ {（1）}〜=〜\ left（1- \ beta _ {\ mathrm {s}} ^ {（1）} \ right）/ 2 \）は、定式化をさらに単純化するために使用されます。数値計算が簡単なため、初期形状として正方形を選択しました。円など、他の任意の幾何学的形状を考慮することができます。別の形状を選択した場合の影響は、フォームファクタのPorod領域でのみ観察されます。これは、このホワイトペーパーの範囲を超えています。

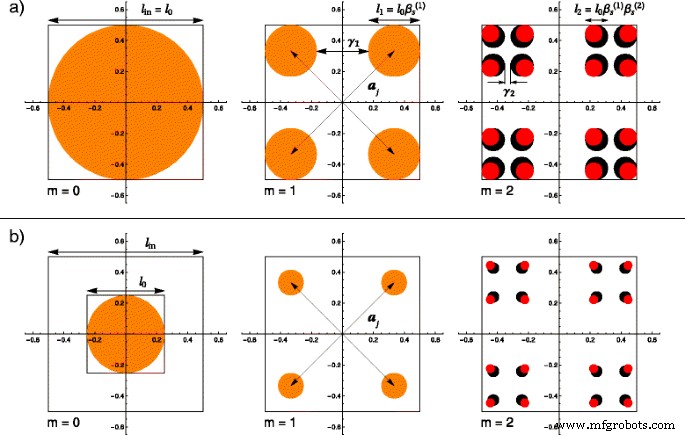
（オンラインカラー）最初の2回の反復での通常のフラクタルとファットフラクタルの比較。ここで、 m の基本形状 =0は直径 l のディスクです ₀ フラクタルサイズは l _in ： a l ₀ = l _in ; b l ₀ = l _in / f 、 f を使用 =2.どちらの場合も、 m で =1スケーリング係数が等しいため、構造は一致します\（\ beta _ {\ mathrm {s}} ^ {（1）} \）。 m で始まる =2、ファットフラクタルのスケーリング係数は大きくなります\（\ left（\ beta _ {\ mathrm {s}} ^ {（2）}> \ beta _ {\ mathrm {s}} ^ {（1）} \右）\）、したがって、ディスクの直径は大きくなります（黒いディスク ）通常のフラクタル（赤いディスク）の場合よりも ）; a _j は位置ベクトルとγです _i i で削除された長さの割合です 3回目の反復

上記の最初の2つの手順は、反復 m の場合、ファットフラクタルのクラシックバージョンの構築にも適用されます。 =0および m =1.これが、これまで、これら2つの構造が一致する理由です。ファットフラクタルを取得するために、反復 m で使用されるアルゴリズムの変更 =1は、 m で別のスケーリング係数を選択して実行する必要があります =2、\（\ beta _ {\ mathrm {s}} ^ {（2）} \ equiv（1- \ gamma _ {2}）/ 2 \）。反復回数が多い場合にアルゴリズム全体を適用すると[34、35]、古典的なバージョンのファットフラクタルが再取得されます。構造から明らかなように、各反復でスケーリング係数が等しくなるように選択された場合、フラクタルの通常のバージョンが復元されます\（\ beta _ {\ mathrm {s}} ^ {（1）}〜=〜 \ beta _ {\ mathrm {s}} ^ {（2）}〜=〜\ cdots =\ beta _ {\ mathrm {s}} ^ {（m）} \）。

SAS強度の振る舞いにおける2つのべき乗則の崩壊の間の一定のプラトーを得るために、散乱ユニット間の距離がそれらの全体のサイズよりもはるかに大きいことを考慮に入れる必要があります。このようなアプローチは、最初に表面フラクタルモデルのコンテキストで使用されました[36、37]。比率 f を考慮する 散乱ユニット間の全体的な距離の l _in とその全体のサイズ l ₀ 、1つは：

2つのフラクタル領域間で一定の強度のプラトーを表示する散乱実験の場合、 f の値 ≫1を選択する必要があります。表面フラクタルの場合、 f の値を増やします 一方では総SAS強度と、他方では独立した散乱単位の近似との間のより良い一致につながります[36、37]。

上記の考慮事項を使用して、通常のフラクタルと脂肪フラクタルの違いを説明できます。因子 f の影響 上で紹介した、も視覚化できます。これが、図1で、半径 r のディスクを使用した比較をグラフで例示している理由です。 ₀ ≡ l ₀ / 2 = l _in /（2 f ）私たちの基本的な形として。図1の各行に表示されている最初の2回の反復の結果は、通常のフラクタル（赤いディスクでマーク）とファットフラクタル（黒いディスクで表されている）で得られた構造を表しており、これらも完全にオーバーレイできます（オレンジ色のディスクとしてマークされています）。図1aのラベルが付いた行では、係数 f 古典的な構造とフラクタル形状が得られるように、単位と等しいと見なされます。図1bで示される図の2行目は、上記の要因の影響を示しています。これらの計算では、 f の任意の値を選択しました =2。反復で m であることがわかります =0および m =1、aとbの両方の場合で、得られた通常のカントール集合と太いカントール集合の構造は同一であり、完全にオーバーレイされています。これは、一般的な倍率のために予想されます。ただし、図1の最後の画像ペアに見られるように、 m で始まります。 =2、ファットフラクタルのディスクの半径は、そのスケーリング係数\（\ beta _ {\ mathrm {s}} ^ {（2）} \）が通常のものよりも定義上大きいため、大きくなります。図2bの最後の画像では、係数 f の値が単一ではないため、ディスクのサイズは図2aの対応する画像よりもはるかに小さくなっています。 。

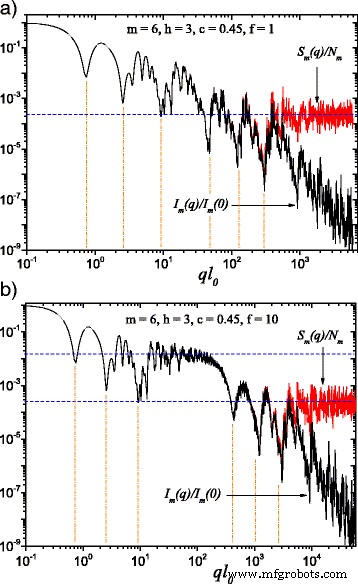
（オンラインカラー）式で与えられる散乱強度の比較。 （22）（黒い曲線 ）および式で与えられる構造因子。 （24）（赤い曲線 ） m で =6であり、式（1）に従って方向全体で平均化されます。 （25）。ここで、 h =3（つまり、スケーリング係数は3回の連続した反復で一定に保たれます）、散乱強度を計算する際の基本的な形状は、エッジサイズの2乗です l ₀ ： a l ₀ = l _in ; b l ₀ = l _in / f （ f を使用 =10）。 f の場合 ≠1、2つの一般化されたべき乗則の減衰の間に一定の強度のプラトーが現れます（図2b）。 水平線 構造因子≃1/ N の漸近線を示します _m 、最小位置は式（1）に従って推定されます。 （26）

べき乗則自体を取得するには、古典的な脂肪フラクタルモデルをさらに一般化する必要があります。これは、スケーリング係数の変更がすべての反復で行われるのではなく、2番目、3番目、⋯、または一般的には h ごとに行われることを考慮して行われます。 3回目の反復。 m で削除された長さの割合 3番目の反復は次のとおりです。

0 < c <1。関数 p _m は次のように定義されます：

m の正の整数値の場合 、 h =1、⋯、 m 、床関数⌊⋯⌋が使用された場所。したがって、 m に対応する倍率 3番目の反復は次のように与えられます：

関数 p の目的が明らかになりました _m h のスケーリング係数を一定に保つことです 反復（ h < m 。

各正方形の位置ベクトルの成分は、次のように書くことができます。

一方、各正方形の辺の長さは次の式で与えられます：

係数 f 長さ l の式で使用されます ₀ （ h の間の反復については、それを考慮に入れます。 +1）番目と m th、正方形のサイズはそれらの間の距離に応じて減少します：

ここで h < m 。各反復での正方形の数は次のとおりです。

したがって、一定のスケーリング係数での反復と見なされるすべてのスケールで、[29、38、39]で与えられる異なるフラクタル次元があります。

反復回数が多い場合、構築されたフラクタル集合のフラクタル次元は[34]になります。

これは、2次元のファットフラクタルの期待値です。最後に、 a の場合 _i i で削除された相対領域です 3回目の反復、\（\ prod _ {i =1} ^ {m}（1-a_ {i}）> 0 \）if \（\ sum _ {i =1} ^ {\ infty} a_ {i} <\ infty \）、したがって、モデルは脂肪フラクタルの定義と特性を満たします[35]。

結果と考察

バビネの原理によれば、 m でそれを結論付けることができます 反復では、格子の開口部はフラクタルの残りの正方形ですが、削除された部分は放射に対して不透明になります。

単分散散乱強度と構造因子

脂肪カンターフラクタルの散乱強度の解析式を導出するために、1 D に対応する任意の反復に対する格子透過率の漸化式を記述することから始めます。 場合。 m で =0、

フラクタルの構築アルゴリズムを考慮に入れると、最初の反復後の透過率は次の式で与えられます。

$$ \ begin {aligned} T_ {1}（l_ {1}、x、）=T_ {0}（l_ {1}、x）\ ast \ delta \ left（\ frac {x-l_ {0} \ beta _ {\ mathrm {t}} ^ {（1）}} {l_ {1}} \ right）+ \\ T_ {0}（l_ {1}、x）\ ast \ delta \ left（\ frac {x + l_ {0} \ beta _ {\ mathrm {t}} ^ {（1）}} {l_ {1}} \ right）、~~~~~~~~~~~~ \ end {aligned} $$ （17）

ここで、δ （ x − a ）は、 x での1次元のディラックのデルタ分布です。 = a 。記号∗は畳み込み演算子を表します。したがって、 m で 3回目の反復では、次のように記述できます。

$$ \ begin {aligned} T_ {m}（l_ {m}、x）=T_ {m-1}（l_ {m}、x）\ ast \ delta \ left（\ frac {x-u_ {m} } {l_ {m}} \ right）+ \\ T_ {m-1}（l_ {m}、x、y）\ ast \ delta \ left（\ frac {x + u_ {m}} {l_ {m }} \ right）、~~~~~~~~~~~~ \ end {aligned} $$（18）

ここで、\（u_ {m}〜=〜l_ {0} \ beta _ {\ mathrm {t}} ^ {（m）} \ prod _ {j =1} ^ {m-1} \ beta _ {\ mathrm {s}} ^ {（j）} \）。式でフーリエ変換を実行します。 （18）、 m での散乱振幅が 3番目の反復は次のとおりです。

$$ A_ {m}（p）=2 ^ {m} \ frac {\ sin（\ pi p l_ {m}）} {\ pi p l_ {m}} \ prod \ Limits_ {i =1} ^ { m} \ cos（2 \ pi p u_ {i}）。 $$（19）

2 D 以降 ファットフラクタルモデルは、2つの1次元ファットフラクタルの直接積であり、そのフーリエ変換は、2つの1次元フーリエ変換の積として記述できます。したがって、2次元散乱振幅は次のように書くことができます。

$$ A_ {m}（p、s）\ equiv A_ {m}（p）A_ {m}（s）、$$（20）

したがって、

$$ \ begin {aligned} A_ {m}（p、s）=N_ {m} \ frac {\ sin（\ pi p l_ {m}）} {\ pi p l_ {m}} \ frac {\ sin （\ pi s l_ {m}）} {\ pi s l_ {m}} \ times \\ \ prod \ Limits_ {i =1} ^ {m} \ cos（2 \ pi p u_ {i}）\ cos （2 \ pi s u_ {i}）、\ end {aligned} $$（21）

散乱強度が次のようになるようにします。

$$ \ begin {aligned} I_ {m}（p、s）=\ left（\ frac {\ sin（\ pi p l_ {m}）} {\ pi p l_ {m}} \ frac {\ sin（ \ pi s l_ {m}）} {\ pi s l_ {m}} \ right）^ {2} \ times \\ N_ {m} ^ {2} \ left（\ prod \ Limits_ {i =1} ^ {m} \ cos（2 \ pi p u_ {i}）\ cos（2 \ pi s u_ {i}）\ right）^ {2}。 \ end {aligned} $$（22）

前の式の最初の係数は、式（1）で述べられているように、フォームファクターによる回折強度を表します。 （5）：

$$ F_ {m}（p、s）=\ left（\ frac {\ sin（\ pi p l_ {m}）} {\ pi p l_ {m}} \ frac {\ sin（\ pi s l_ { m}）} {\ pi s l_ {m}} \ right）^ {2}、$$（23）

エッジの単一の正方形から得られる散乱強度に対応します l _m 。式（1）で述べられているように、構造因子による回折強度を表す2番目の因子。 （5）：

$$ S_ {m}（p、s）=N_ {m} ^ {2} \ left（\ prod \ Limits_ {i =1} ^ {m} \ cos（2 \ pi p u_ {i}）\ cos （2 \ pi s u_ {i}）\ right）^ {2}、$$（24）

正方形が分散される方法を説明します。総散乱放射線強度は、 F の積です。 _m （ p、s ）および S _m （ p、s 。

式（1）で定式化された、強度のべき乗則の減衰。 （22）は、すべての方向の平均を実行した後に取得されます[29]。任意の方向の確率が等しいことを考慮すると、2次元フラクタルの場合、散乱ベクトルのすべての方向を積分することで平均を計算できます q =（ p、s ）：

$$ \ langle f（p、s）\ rangle =\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} f（q、\ phi）\ mathrm {d} \ phi、$ $（25）

ここで p = q cos ϕ および s = q sin ϕ 。したがって、散乱強度 I （ q ）は、運動量伝達係数 q の関数として取得されます。 ≡| q |。

なぜなら、構造因子の定義から、\（S_ {m}（0）〜=〜N_ {m} ^ {2} \）があり、ここで N _m 式で定義されているように、は正方形の数です。 （13）、正規化の標準手順 S _m （0）=1は、[11、29]で説明されているように採用できます。

単分散散乱強度 I に対して計算された結果 _m （ q ）および構造因子 S _m （ q ）、 m =6は、古典的な脂肪フラクタル（ f ）について図2に表示されています。 =図2a）の1であり、この作業で開発された拡張脂肪フラクタルモデルの場合（ f =図2b）の10。図2bを取得するために、 h を検討しました。 =3であるため、最初の3回の反復のスケーリング係数\（\ beta _ {\ mathrm {s}} ^ {（1）} \）は一定に保たれ、その後、他の定数値\（\ beta _ {\ mathrm {s}} ^ {（2）} \）次の3回の反復。予想どおり、どちらの場合も（ f の場合） =1および f =10）、一方の散乱強度と他方の構造因子の違いは、\（q \ gtrsim 1 / l_ {m} \）のときに観察できます。この領域では、散乱強度にはべき乗則の減衰があります I （ q ）∝ q ^-3 。構造因子の漸近値は1 / N になる傾向があります _m 、図2aの水平線または図2bの下の水平線で表されます[29、33]。

図2aに、単純なべき乗則の減衰に対する、最大値と最小値の重ね合わせとして識別できる2つの一般化されたべき乗則の減衰の連続を示します。しかし、図2bでは、ドメイン20≲ ql のほぼ一定の強度の領域です。 ₀ ≲100は明確に区別でき、2つの連続する一般化されたべき乗則の崩壊に含まれます。これは、正方形のサイズが1桁（ f ）減少したためです。 =10）それらの間の距離と比較して。図2bの上部の水平線の周りで観察できるこの領域には、漸近線1 / N があります。 ₃ 、古典的なファットフラクタルの構造因子の1つと同じで、最初の3回の反復のみを考慮した場合と同様の動作を示します。

さらに、図2から、各スケールでの最小値の数が、一定のスケーリング係数の反復回数と一致していることがわかります。これらの最小値は、フラクタル内のさまざまな正方形を通過する放射線が干渉し、位相が逆になっている場合に発生します。したがって、正方形の中心間で最も頻繁に遭遇する距離（2 u _m ）はπと同じです / q 。これが、最小値のおおよその位置が次の関係から得られる理由です。

$$ q_ {i} \ simeq \ frac {\ pi} {2 u_ {i}}、~~~~ i =1、\ cdots、m $$（26）

図2に縦線で示されています。最初の6回の反復では、式（1）を使用して計算された位置の間に非常に良い一致が見られます。 （26）、および散乱強度、または構造因子に見られるもの。この近似は、反復回数が特定の値を超えると、反復回数が増えると精度が低下する可能性があります。これらの場合、最も頻繁に遭遇する距離に匹敵する距離が増えるためです。それにもかかわらず、この近似は実際にはかなりうまく機能するはずであり、そのような最小値を4つまたは5つ以上区別することはほとんど期待できません。

個々のスケールごとに、指定された範囲1 /（2 u _i ）≲ q ≲1/（2 u _{i +1} ）、回折パターンは i のみの干渉によって生成されます フラクタル反復。これを使用して、この間隔内で関数 I が機能することを示すことができます。 _m （ q ） q ^D および S _m （ q ） q ^D 対数周期[29]であり、 D は、特定のスケールに対応するフラクタル次元です。特に、図１および２に示される結果については、 2と3、関数 I _m （ q ） q ^−1.1 および S _m （ q ） q ^−1.1 I である間、最初の3回の反復では周期\（1 / \ beta _ {\ mathrm {s}} ^ {（1）} \）で対数周期です。 _m （ q ） q ^−1.51 および S _m （ q ） q ^−1.51 3回の反復の2番目のグループでは、\（1 / \ beta _ {\ mathrm {s}} ^ {（2）} \）で対数周期です。

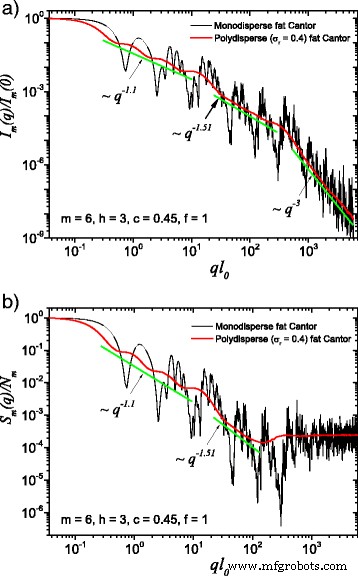
（オンラインカラー）単分散システムと多分散システムの比較： a 散乱強度（式（22））; b 構造因子（式（24））は、式（24）に従って、フラクタルのすべての方向で平均化されます。 （25）。ここで、 f =1、 m =6、 h =3（つまり、スケーリング係数は3回の連続した反復で一定に保たれます）、基本形状は初期エッジ長の2乗 l ₀ = l _in 。どちらの場合も、多分散性は単分散散乱曲線を塗りつぶし、フラクタル次元は各構造レベルで回復できます

決定論的質量フラクタルと同様の方法で、式。 （26）は、脂肪フラクタルを特徴付けるいくつかの構造パラメータを取得するために使用できます。まず、最小値の総数はフラクタル反復の総数と一致します。図2は、フラクタルが倍率\（\ beta _ {\ mathrm {s}} ^ {（1）} \）の3回の反復と、倍率\（\ beta _ {\ mathrm {s}）の3回の反復で構成されていることを示しています。 } ^ {（2）} \）。第二に、これらの最小値の周期性から（または I の周期性から） _m （ q ） q ^D および S _m （ q ） q ^D ）、スケーリング係数を回復できます。図2bでは、スケーリング係数\（\ beta _ {\ mathrm {s}} ^ {（1）} \）は、 ql での最小値の周期性から取得できます。 ₀ ≃7、25、および90、スケーリング係数\（\ beta _ {\ mathrm {s}} ^ {（2）} \）は、 ql での最小値の周期性から取得できます。 ₀ ≃400,1000および2500。さらに、フラクタル領域間の中間プラトーの長さは、比率（ f ）の指標として使用できます。 ）散乱ユニット間の距離、およびそれらの全体的なサイズ。図2bでは、この範囲は13≲ ql に対応します。 ₀ ≲130。

多分散散乱強度と構造因子

作業のこの部分では、格子サイズが分布関数 D に従っていると見なすことができます。 _N （ l ₀ ）、 D となるように定義されています _N （ l ₀ ）d l ₀ フラクタル格子のサイズが区間（ l ）にある確率を示します ₀ 、 l ₀ + d l ₀ ）。このステップでは、脂肪フラクタルモデルに多分散度を導入します。対数正規分布を選択することでこれを例示します：

$$ D _ {\ mathrm {N}}（l_ {0}）=\ frac {1} {\ sigma l_ {0}（2 \ pi）^ {1/2}} e ^ {-\ frac {\ left （\ log（l_ {0} / \ mu）+ \ sigma ^ {2} / 2 \ right）^ {2}} {2 \ sigma ^ {2}}}、$$（27）

相対分散付き\（\ sigma _ {\ mathrm {r}} =\ left（\ left \ langle l_ {0} ^ {2} \ right \ rangle _ {D}-\ mu ^ {2} \ right）^ {1/2} / \ mu \）、平均値μ =〈 l ₀ 〉 _D 、および分散\（\ sigma =\ left（\ log \ left（1+ \ sigma _ {\ mathrm {r}} ^ {2} \ right）\ right）^ {1/2} \）。式を使用します。 （21）と（27）は、分布関数全体で平均化された多分散強度を取得します。

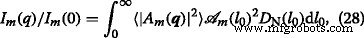
どこ 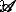は、 m の対応する領域です。 3回目の反復。構造因子は同様の方法で計算されますが、項はありません 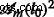[29]。

多分散（赤い曲線）および単分散（黒い曲線）の散乱強度（aでラベル付け）および構造因子（bでラベル付け）の場合の計算結果を図1および2に示します。 3と4。それらの違いは、 f の値によって与えられます。 要素。図3では、ファットフラクタルの古典的な構造が使用され、 f =1、基本単位のサイズが小さいことを考慮しながら、 f を選択することになります =図4の10。多分散度は、σの相対分散に対して計算されます。 _r =0.4。振動が不鮮明になり、全体の振幅が減少するため、散乱曲線が滑らかになることがわかります[29、40]。ただし、σのこの特定の値の場合 _r 、主な最小値と最大値の位置はまだ観察可能です。

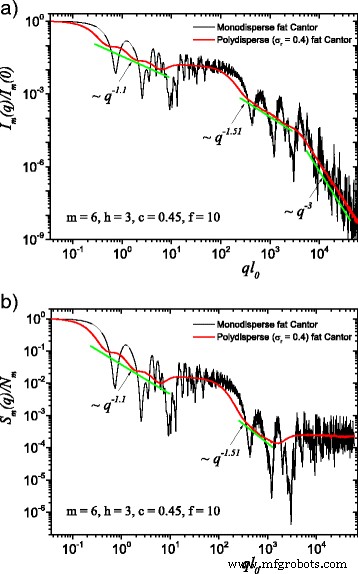
（オンラインカラー）単分散システムと多分散システムの比較： a 散乱強度（式（22））; b 構造因子（式（24））は、式（24）に従って、フラクタルのすべての方向で平均化されます。 （25）。ここで、 f =10（したがって、一定の強度の領域は約20≲ ql に現れます ₀ ≲100）、 m =6、 h =3（つまり、スケーリング係数は3回の連続した反復で一定に保たれます）、基本形状は初期エッジ長の2乗 l ₀ = l _in 。どちらの場合も、多分散性は単分散散乱曲線を塗りつぶし、フラクタル次元は各構造レベルで回復できます

より一般的には、σの値が小さい場合 _r （つまり、振動が観測できるほど小さい）、式（1）で与えられる推定値。 （26）は引き続き使用できます。したがって、フラクタル反復の数、各構造レベルでのスケーリング係数、散乱ユニット間の距離の比率、およびそれらの全体的なサイズを回復できます。 σの場合 _r 振動が完全に不鮮明になるように十分に高い値に増加すると、散乱曲線は単純なべき乗則の減衰になります。狭いベル型の分布を使用したため、散乱指数が保持されます。さらに、べき乗則の減衰ごとに、その特定の構造レベルのフラクタル次元が得られます。これは、式（1）の理論的推定とよく一致しています。 （14）。これは、ほとんどすべての散乱曲線がある程度の多分散性を持っている実験設定にも一致しています。したがって、一定の強度のインターリーブ領域を備えた開発済みの脂肪フラクタルモデルは、多分散実験データから各構造レベルでフラクタル次元を回復します。

結論

この記事では、ナノスケールの脂肪フラクタルの標準モデルを一般化する理論モデルを提案します。これは、基本ユニットの形状の初期エッジサイズがフラクタルの全体のサイズよりもはるかに小さく、したがってフラクタル内の基本ユニット間の距離よりもはるかに小さいという事実によって特徴付けられます。図1bは、これらの量の中間にそれぞれ1/2の商を考慮した場合の、基本モデルを示しています。

このモデルに基づいて、分析式が計算され、式（1）に示されます。 （22）散乱強度については、式（22）を参照してください。 （24）構造因子。可能なすべての方向の平均化は、式（1）に従って行われます。 （25）。これらの平均量は、2つの対数スケールで、2つの構造レベルの存在によって特徴付けられます。したがって、図1および2に示すように、プラトーで表される一定の強度の領域によってインターリーブされた2つのべき乗則の減衰によって特徴付けられます。 2 bおよび4。このプラトーは、スケーリング係数が一定に保たれている場合に、最初の構造レベルからの寄与のみを考慮したかのように、脂肪フラクタルの構造因子の漸近領域と一致します。プラトーの漸近値を使用して、各構造レベルの散乱単位の数を取得できます。プラトーの長さは、 f の値によって制御されます。 。プラトーを含むべき乗則の減衰は、有限数の反復、この例では、合計6つのうち3つについて、スケーリング係数を一定に保つことによって得られます。スケーリング係数の値は、定義上、各構造レベルで増加するため、2番目のべき乗則の減衰の傾きは大きくなります。これは、図1および2に示すように、数値計算によって確認されます。 2、3、および4。

また、脂肪フラクタルモデルの多分散の場合についても説明しました。ここで、構成単位のサイズは、例として、対数正規分布関数に従います。散乱強度と構造因子の平滑化された曲線が得られました。相対分散の値が十分に小さい単分散散乱曲線と多分散散乱曲線により、スケーリング係数を取得できます。 各構造レベルで、多分散曲線の散乱指数はフラクタル次元を示します。 各構造レベルで。相対分散に選択された値0.4は、散乱特性の最小値がまだ観察でき、曲線がべき乗則の減衰に近い形状を保持している場合を示すためのものです。

提案されたモデルのフレームワークで得られた結果は、フラクタル次元の変化の規則的な法則によって特徴付けられるフラクタル材料の構造特性を明らかにするために使用できます。提案されたモデルは、基本ユニットのさまざまな形状、3つ以上の構造レベルなどの他の機能を含めるように拡張したり、他のユークリッド次元で機能するように適合させたりできるため、非常に用途の広いモデルでもあります。これらの結果は、さまざまな複雑なナノおよびマイクロスケールの階層構造から得られた小角散乱のコンテキストでの実験的な回折データの詳細な説明に役立ちます。

付録

フラクタル次元

質量とそれぞれの表面フラクタル次元は、おそらくフラクタルを特徴付ける最も重要な量です。実際には、決定論的な質量フラクタルのみを扱い、質量フラクタル次元を単にフラクタル次元（ D ）と呼びます。 _m 。

一般的に、質量半径 関係は[2]のように書き直すことができます：

ここで、スケーリング則の修正 A （ r ） r の場合、定数値になる傾向があります →∞ 。

構造が上限数のフラクタルであることがアプリオリにわかっている場合、フラクタル次元は最初の反復から直接見つけることができます。この手順を説明するために、サイズ l のフラクタルを考えてみましょう。 ₀ 、 k で構成されます 最初の反復での基本単位、それぞれのサイズはβ _s l ₀ 、ここでβ _s はスケーリング係数です。 質量半径以降 関係、式で与えられます。 （29）は、スケール不変性と同等です。 関係[2]：

M と書くことができます （ l ₀ ）= kM （β _s l ₀ ）。式を使用して。 （29）、次の方法でフラクタル次元を計算する直接法を取得します。

フラウンホーファー回折と配列定理

2次元の回折アパーチャΣを考えてみましょう。 、（ x、y ）平面、正の z で照らされます 方向。観測面（ u、v ）、Σと平行 、ホイヘンス・フレネル原理に従って、回折のスカラー理論のフレームワークを使用して計算された、得られた回折画像の複素数値の振幅は、[41]と書くことができます。

前の式で、\（r =\ sqrt {z ^ {2} +（ux）^ {2} +（vy）^ {2}} \）は、平面からそれぞれ取られた2つの任意の点の間の距離です。 Σを含む そして観測面から。フラウンホーファー回折モデルを適用するには、この距離が波長λよりもはるかに大きいという条件を満たす必要があります。 。

式（1）の平方根の二項式展開を実行します。 （32）最初の2つの項のみを保持すると、[41]が得られます。

この近似により、フレネル回折積分が得られます。

ここで、プリファクター P （ u、v ）は

および k =2 π / λ 。さらに、条件 z ≫ k Max（ x ² + y ² ）/ 2が満たされ、\（\ text {Exp} {\ left（\ frac {k} {2z}（x ^ {2} + y ^ {2}）\ right）} \ simeq 1 \）があります。式を書き換えます。 （34）、フラウンホーファー近似は次のようになります。

p で空間周波数を表す = u /（λ z ）および s = v /（λ z ）そして乗法位相因子 P を無視します （ u、v ）式の積分の前に。 （36）、振幅は単純にΣの分布のフーリエ変換になります 絞り。照明が法線入射で単色の単位振幅平面波を使用して行われ、開口部全体の電界分布がその透過関数 T に等しいことを考慮すると （ x、y ）、位相空間での回折振幅の度数分布を取得します。