10進数からの変換

8進数と16進数の記数法には、2進数の倍数の基数（基数2）があるため、16進数または8進数と2進数の間の変換は非常に簡単です。

また、10進法に精通しているため、2進数、8進数、または16進数を10進数形式に変換するのは比較的簡単です（暗号値と桁の重みの積を合計するだけです）。

ただし、10進数からこれらの「奇妙な」記数法への変換は別の問題です。

トライアルアンドフィット方式

おそらく最も理にかなっている方法は、「試行と適合」法です。この方法では、10進形式で表される目的の値に、2進、8進、または16進表記を「適合」させようとします。

たとえば、87の10進値を2進形式で表現したいとします。まず、場所の重みの値を含む2進数のフィールドを描画します。

ええと、128の代わりに「1」ビットがないことはわかっています。これは、すぐに87より大きい値を取得するためです。

ただし、右側の次の重み（64）は87未満であるため、そこに「1」が必要であることがわかります。

右側の次の場所も「1」にすると、合計値は64 ₁₀ になります。 + 32 ₁₀ 、または96 ₁₀ 。これは87 ₁₀ より大きい 、したがって、このビットは「0」でなければならないことがわかります。

次の（16の）桁を「1」に等しくすると、合計値は64 ₁₀ になります。 + 16 ₁₀ 、または80 ₁₀ 、これは目的の値（87 ₁₀ ）に近いです ）それを超えることなく：

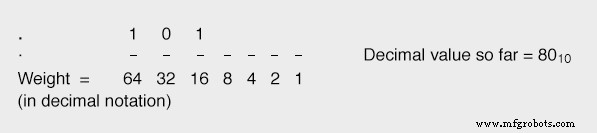
この進行を継続し、必要に応じて各軽量ビットを設定して、それを超えずに目的の合計値に到達することで、最終的に正しい数値に到達します。

8進数および16進数での試行と適合の方法

このトライアルアンドフィット戦略は、8進数と16進数の変換でも機能します。同じ10進数の87 ₁₀ を見てみましょう。 、8進数に変換します：

64の代わりに「1」の暗号を配置すると、合計値は64 ₁₀ になります。 （87 ₁₀ 未満 ）。 64の場所に「2」の暗号を配置すると、合計値は128 ₁₀ になります。 （87 ₁₀ より大きい ）。これは、8進数の数え上げが64の位の「1」で始まる必要があることを示しています。

ここで、8の代わりに暗号値を試して、87にできるだけ近い合計（10進数）値を超えないようにする必要があります。最初のいくつかの暗号オプションを試してみると、次のようになります。

8の代わりに「3」の暗号値を指定すると、必要な合計87 ₁₀ を超えることになります。 、つまり「2」です！

もちろん、8進数/ 2進数の変換に関する最後のセクションで注意を払っていた場合は、（10進数の）87 ₁₀ の2進数表現を使用できることに気付くでしょう。 、以前は1010111 ₂ であると判断しました 、そしてそれから8進数に簡単に変換して、作業を確認します：

10進数から16進数への変換も同じように実行できますか？もちろんですが、誰がしたいですか？この方法は理解しやすいですが、実行するのは面倒です。

これらの変換を行う別の方法があります。これは基本的に同じですが（数学的には）、簡単に実行できます。

繰り返し分割テクニック

この他の方法では、（10進表記を使用して）除算の繰り返しサイクルを使用して、10進数を2進数、8進数、または16進数の桁の重み値の倍数に分割します。

除算の最初のサイクルでは、元の10進数を取得し、変換先の記数法の基数で除算します（binary =2 Octal =8、hex =16）。

次に、除算結果の整数部分（商）を取得し、それを再び基数で除算します。以下同様に、商が1未満になるまで続けます。

2進数、8進数、または16進数は、各除算ステップで残った「余り」によって決定されます。これがバイナリでどのように機能するかを見てみましょう。10進数の例は87 ₁₀ ：

バイナリビットは、LSBから始まり、MSBに進む、連続する除算ステップの余りから組み立てられます。この場合、1010111 ₂ の2進表記に到達します。 。

2で割ると、常に「.0」または「.5」で終わる商、つまり0または1の余りが得られます。前述のように、この変換の繰り返し除算手法は、数え上げに有効です。バイナリ以外のシステム。

8進数に変換するために8など、異なる数値を使用して連続した除算を実行する場合、必ず0から7までの余りが得られます。同じ10進数87 ₁₀ でこれを試してみましょう。 ：

1未満の数量を処理する記数法を変換するためにも、同様の手法を使用できます。

1未満の10進数を2進数、8進数、または16進数に変換するには、繰り返し乗算を使用し、各ステップの積の整数部分を変換された数値の次の桁とします。

10進数0.8125 ₁₀ を使用しましょう 例として、バイナリへの変換：

整数の繰り返し除算プロセスと同様に、各ステップで「ポイント」からさらに離れた次の桁（またはビット）が得られます。

整数（除算）では、LSBからMSB（右から左）に作業しましたが、乗算を繰り返すと、左から右に作業しました。

1より大きい10進数を1未満のコンポーネントで変換するには、両方を使用する必要があります。 テクニック、一度に1つずつ。 54.40625 ₁₀ の10進数の例を見てください 、バイナリへの変換：

関連するワークシート：

• 記数法ワークシート