公差スタッキングのベストプラクティス

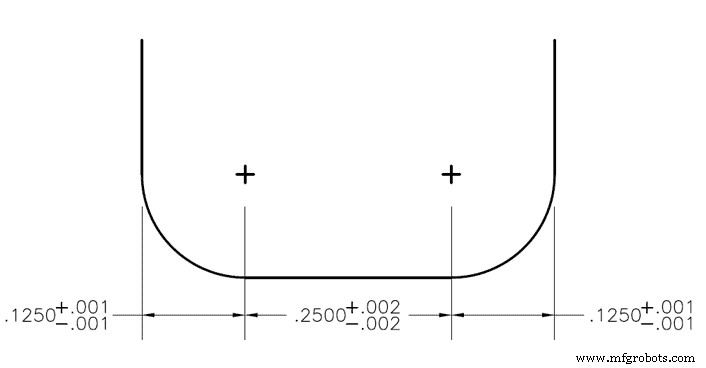
部品のすべてのフィーチャーに上限と下限の公差がラベル付けされている場合、寸法超過が問題になる可能性があります。たとえば、右と左のコーナー半径を持つコーナー半径エンドミルの許容誤差は+/- .001インチであり、それらの間のフラットの許容誤差は.002インチです。この場合、カッター直径の許容範囲ウィンドウは+/- .004インチになりますが、部品の寸法記入中に誤って計算されることがよくあります。さらに、このコールアウトに公差を設定すると、寸法が大きくなりすぎるため、公差の代わりに参照寸法「REF」を残す必要があります。

統計的公差分析を利用する：

統計分析では、標準偏差に基づいて、3つの公差すべてが寸法スロット幅より下または上になる可能性を調べます。この確率は、正規確率密度関数で表されます。これは、下の図2に示されています。設計でさまざまな部品と寸法のすべての確率を組み合わせることにより、部品の寸法と公差に基づいて、部品に問題があるか、完全に故障する確率を判断できます。通常、この分析方法は、公差が4つ以上のアセンブリにのみ使用されます。

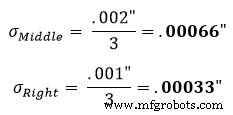
統計的公差分析を開始する前に、公差分布係数を計算または選択する必要があります。標準分布は3です。これは、ほとんどのデータ（またはこの場合は許容誤差）が平均の3標準偏差以内にあることを意味します。すべての許容誤差の標準偏差をこの許容誤差分布係数で割って、3の分布から1の分布に正規化する必要があります。これが完了すると、ルートの合計の2乗を使用して、アセンブリの標準偏差を見つけることができます。

3つの異なるサイズの豆で作られた一杯のコーヒーのように考えてください。おいしい一杯のジョーを作るには、まずすべての豆を同じサイズに粉砕して、コーヒーフィルターに追加できるようにする必要があります。この場合、豆は標準偏差であり、グラインダーは許容誤差分布係数であり、コーヒーフィルターは二乗和の二乗方程式です。一部の公差は、公差範囲の狭さに基づいて異なる分布係数を持つ可能性があるため、これが必要です。

統計分析方法は、スロットの幅が.500インチ、許容誤差が+/- .003インチである必要があるが、半径（.125インチ）とフラット（.250インチ）が必要ない場合に使用されます。 ）スロット内に収まる限り正確に。この例では、標準偏差がすでに利用可能な3つの両側公差があります。それらは両側性であるため、平均からの標準偏差は、+または–の許容値が何であれ単純になります。外側の半径の場合、これは.001 "になり、中央の平坦な領域の場合、これは.002"になります。

この例では、式1を使用して各セクションの標準偏差（σ）を求めます。この式では、標準偏差を表します。

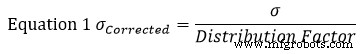
標準的な仮定では、部品の公差は+/-3の正規分布を表します。したがって、分布係数は3になります。図1の左側のセクションの式1を使用すると、修正された標準偏差は次のようになります。

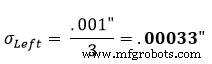
次に、これを中央と右のセクションで繰り返します。

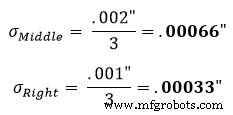
これらの標準偏差に到達した後、結果を式2に入力して、許容範囲の標準偏差を求めます。式2は、二乗和の二乗方程式として知られています。

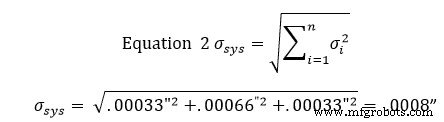
この時点で、スロットの68％が+/-.0008インチの許容範囲内にあることを意味します。この許容誤差に2を掛けると、95％の信頼ウィンドウになり、3を掛けると、99％の信頼ウィンドウになります。

スロットの68％は+/-.0008インチ以内になります

スロットの95％は+/-.0016インチ以内になります

スロットの99％は+/-.0024インチ

これらの信頼ウィンドウは、通常の分散データポイントセットの標準です。標準の正規分布を上の図2に示します。

統計公差解析は、公差部品が4つを超えるアセンブリにのみ使用する必要があります。この単純な分析では、多くの要因が考慮されていませんでした。この例は、許容誤差が平均からの標準偏差を表す3つの両側次元の場合です。標準の統計公差分析では、角度、振れ、平行度など、補正係数を必要とする他の変数が関係します。

Harvey Performance Companyのブランドが業界のプレミアカムソフトウェアプロバイダーと提携して、ツールライブラリを提供していることをご存知ですか？

詳細はここをクリック

最悪のケースの分析を使用する：

最悪の場合の分析は、部品のすべての公差を合計して、部品の総公差を見つける方法です。このタイプの分析を実行する場合、各許容値はそれぞれの範囲で最大または最小の制限に設定されます。次に、この総公差を部品の性能限界と比較して、アセンブリが適切に設計されていることを確認できます。これは通常、1次元のみ（1平面のみ、したがって角度は含まれません）および部品数が少ないアセンブリに使用されます。

最悪のシナリオでは、工具の公差を部品の公差に追加できるため、最悪の場合の分析を使用して、作業に適した切削工具を選択することもできます。このシナリオが特定されると、機械工またはエンジニアは適切な調整を行って、部品を印刷で指定された寸法内に保つことができます。最悪のシナリオが実際の本番環境で発生することはめったにないことに注意してください。これらの分析は製造に費用がかかる可能性がありますが、すべてのアセンブリが適切に機能することを保証することにより、機械工に安心を提供します。多くの場合、この方法では、最大条件でのスタックの合計が設計で使用される主要な機能であるため、厳しい許容誤差が必要になります。公差が厳しくなると、削り取り量の増加、検査のための製造時間、およびこれらの部品に使用される工具のコストが増加するため、製造コストが増大します。

図1に関連する最悪のシナリオの例：

仕様の下限を見つけます。

左隅の半径の場合

.125” – .001” =.124”

フラットセクションの場合

.250” – .002” =.248”

右隅の半径の場合

.125” – .001” =.124”

これらすべてを一緒に仕様の下限に追加します：

.124” + .248” + .124” =.496”

仕様の上限を見つける：

左隅の半径の場合

.125” + .001” =.126”

フラットセクションの場合

.250” + .002” =.252”

右隅の半径の場合

.125” + .001” =.126”

これらすべてを一緒に仕様の下限に追加します：

.126” + .252” + .126” =.504”

2を引き、この答えを2で割ると、最悪の場合の許容誤差が得られます。

（上限–下限）/ 2 =.004”

したがって、このスロットの最悪のシナリオは.500” +/- .004”です。