平面ナノホールスラブを使用した連続体の二重束縛状態によって誘発される高品質係数デュアルバンドファノ共鳴

はじめに

光デバイスの性能向上に重要な光と物質の相互作用の強化は、高品質（Q）ファクターの応答を使用することで実現できます[1]。非対称の線形状と鋭いスペクトルプロファイルを特徴とするファノ共鳴は、光学メタマテリアルで高いQ値を達成するための効果的なアプローチを提供し、大きな注目を集めています[2]。過去10年間で、ファノ共鳴はプラズモンナノ構造によって可能になる多くのナノスケール発振器システムで報告されており[3、4]、ファノ共鳴は金属-誘電体界面での表面プラズマ共鳴によって励起されます。金属メタマテリアルは光操作の有望な候補ですが、プラズモニックメタマテリアルのファノ共鳴は、金属固有のオーム損失のために、通常、可視から近赤外（NIR）スペクトル領域のQ値が低いという問題があります。

一方、全誘電体メタマテリアルは、プラズモンメタマテリアルと同様の誘導変位電流を伴う強力な三重型共鳴を提供しますが、可視からNIRの範囲での散逸損失が少ないという特徴があります[5]。入射光のエネルギーは、電気および/または磁気双極子共鳴の励起により誘電体ナノ構造に高度に局在化する可能性があり、これにより散逸損失が減少し、電場と磁場の両方の大きな共鳴増強が達成されます。近年、連続体の束縛状態（BIC）が、全誘電体メタマテリアルで高Qファクター応答を達成するための最も有望なスキームとして浮上しています[6、7]。 BICは拡張状態の連続スペクトル内に存在しますが、理論的には無限の寿命で、直感に反して完全に空間に局在したままです[8、9]。非放射特性のため、BICは連続スペクトルからは観測できませんが、BICが準BIC（QBIC）に変換されるため、高Qファクターのファノ共鳴を実現できます[10、11]。レイジング[12]、光学フィルター[13]、非線形周波数変換[14]、超高感度センサー[15、16]および光渦ビーム[17]。

一般に、BICの形成は、その干渉性のために、フォトニック構造の対称性（平面および垂直対称性）に強く関連しています。より具体的には、BICは斜め入射または対称性が破られたナノ構造を介して摂動することができ、QBICは固有状態と自由空間の間の放射チャネルが開かれるときに実現できます[18、19]。ただし、非対称ナノクロス[20]、非対称ナノリング[21]、非対称ナノバー[22,23,24]、非対称ナノロッド[25,26、 27,28]、これは、フォトニック構造に深いサブ波長スリット[20,21,22,23,24]またはナノホール[25,26,27,28]を挿入する必要があるため、製造が困難です。再形成された長方形のバー[29、30]などの他のナノ構造は、鋭いエッジが増加しているため、従来のリソグラフィー技術で正確に製造することがより困難になります。追加の漏れのあるチャネル[31、32]。さらに、別のタイプの構造である傾斜ナノバー[33、34]は、ナノファブリケーションプロセスで維持される共振器間の深いサブ波長スペースでナノバーの配向を正確に制御するのが困難です。アプリケーションでは、ナノ構造の平面スラブなどのより単純なアーキテクチャを備えた全誘電体メタマテリアルを使用して、BICと高Qファクターのファノ共鳴を実現することは意味があります[35、36、37、38]。さらに、複数のファノ共鳴は、マルチバンド高調波生成の強化[39]、マルチチャネルセンシング[40]、発光[41]などのアプリケーションで非常に役立ちます。したがって、QBICの励起に基づく比較的単純なアーキテクチャを使用して、高Qファクターの複数のファノ共鳴を実現することには大きな利点があります。

この作業では、四量体化された穴からなる新しい平面ナノホールスラブ（PNS）を提案して、高Qファクターのデュアルバンドファノ共鳴を実現します。超格子の対角線に沿ってPNSの四量体化された穴を縮小または拡大することにより、2つのQBICが励起され、2つのファノ共鳴の位置とそれらのQファクターを柔軟に調整できます。超格子の遠方場多重分解と近接場分布を実行して、PNSの共鳴特性を明らかにします。これは、デュアルバンドファノ共鳴が電気トロイダル双極子または磁気トロイダル双極子間の共鳴結合から生じることを示しています。 PNSのデュアルバンドファノ共鳴は偏光に依存しない機能を備えており、PNSの幾何学的パラメーターが大幅に変更されても存続できるため、潜在的なアプリケーションにより適しています。

メソッド

格子の構造とデザイン

図1は、提案されたPNSの概略形状とその透過スペクトルを示しています。 PNSは、超格子の対角線に沿ってシフト距離Δで縮小（Δ<0）または拡大（Δ> 0）できる4つのナノホールで構成され、Δ=0は周期が半分に短縮された単純な格子に対応します。各ナノホールは、超格子の4分の1の領域の中央にあります。 PNSの周期と高さはそれぞれΛとHです。ナノホールの半径は r 。 PNSの屈折率は n です。 _s =3.2、背景は屈折率 n の空気です _a =1.図1cは、Δのシフト距離の関数としてのPNSのスペクトルを示しています。ここで、PNSは垂直に入射する x によって照らされています。 -偏光。この論文で提示されているPNSのスペクトルと電磁界分布は、COMSOLMultiphysicsの有限要素法の商用ソフトウェアを使用して計算されています。図1cに示すように、Δ=0の非収縮PNSにはファノ共鳴はありません。ただし、変調度が100％の2つのファノ共鳴（ファノピークとファノディップの透過率の差として定義）は、次の式で取得できます。ナノホールをわずかに縮小または拡大します。非収縮PNSの伝送応答と比較すると、収縮PNSの伝送応答は、側波帯がほぼ同じに保たれている間、急激に変化します。

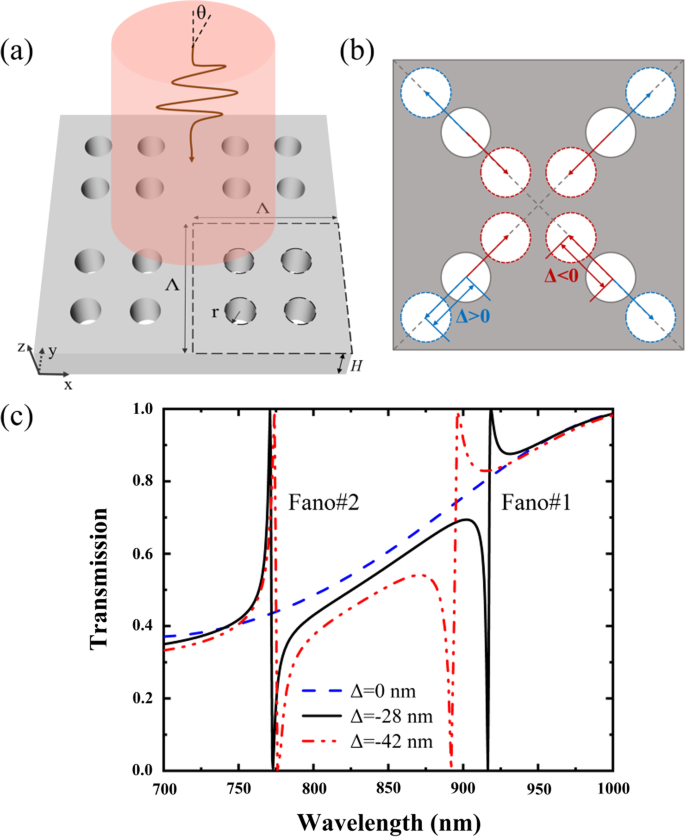
a PNSの斜視図。 b 4つのナノホールが超格子の対角線に沿って縮小（Δ<0）または拡大（Δ> 0）するときのPNSの垂直方向のビュー。 c Δのシフト距離の関数としてのPNSの透過スペクトル。 PNSは x の照明下にあります -入射角がθの偏光入射波 =0。PNSのパラメータは次のとおりです。Λ=350 nm、 r =35nmおよびH =175 nm

四量体化された正孔の収縮または拡大から生じるデュアルバンドファノ共鳴の進展を明確に示すために、Δのシフト距離の関数としてのPNSの透過2Dマップを図2aに示します。図2aに示すように、2つのBICが対象の波長領域でΔ=0として発生し、デュアルBICの同様の現象がデュアルグレーティングメタメンブレン[13]とスプリットリング共振器[21]の構造で以前に報告されました。 Δ≠0の場合、PNSの対称性の破れにより、つまり単純な格子の中心対称性から4回回転（C _{4 ）超格子の対称性。さらに、C 4 四量体化された正孔が超格子の対角線に沿って縮小または拡大されるため、PNSの対称性を維持できます。PNSの透過スペクトルは、同じ絶対値|Δ|に対して同じです。原則として、四量体化された穴の収縮または拡張は、PNSのユニットセルが単純な格子から超格子に変化するときにPNSの最初のブリルアンゾーンの面積を減らします。表面摂動の導入とPNSのブリルアンゾーンフォールディング[42、43]。一般に、対称性が保護されたBICのQファクターは、非対称性の程度に逆二乗依存性を示しますδ 摂動論に基づく[21]：}

ここでĸ は比例定数、 S 超格子の面積ω は角周波数で、非対称パラメータは\（\ delta {=} \ sqrt 2 \ Delta / \ Lambda \）です。

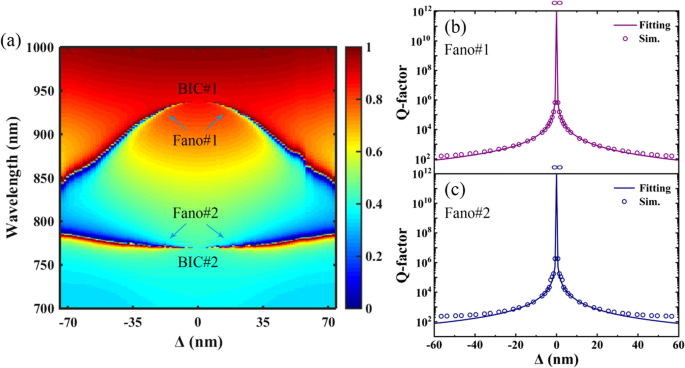
a 超格子の対角線に沿ったΔのシフト距離の関数としてのPNSの透過2Dマップ。 b および c それぞれFano＃1とFano＃2のQファクターとフィッティング結果。その他のパラメータは図1cと同じです

図2b、cは、それぞれFano＃1とFano＃2のQファクターとフィッティング結果を示しています。 PNSのQ値は、共振波長λ間の比率として計算されます。 _r 半値全幅（FWHM）Δλ。ここで、Δλはファノ共鳴のピークとディップの間の波長領域です。 PNSのフィッティング結果は、式（1）を使用して計算されます。 （1）。図2b、cに示すように、Q値がΔ=0で無限大に発散するPNSの発散軌道は、データを適合させるために逆二乗関係を使用して検証されます。優れたフィッティング結果を得ることができ、より大きな非対称性でのわずかな不一致は、式（1）の小さな摂動の仮定からの逸脱によるものです。 （1）。 PNSの重要な利点は、デュアルバンドファノ共鳴の位置とQファクターを、四量体化された正孔を縮小または拡大することで調整できることです。これにより、高Qファクターの複数の共振性能の動的制御が容易になります。ファノ共鳴。

物理的なメカニズムと解釈

PNSの四量体化された正孔を縮小または拡大することによってデュアルバンドファノ共鳴の起源を洞察するために、BICとファノ共鳴の遠方界放射をさまざまな多重極成分の寄与に分解して、それらの機能についてさらに説明します。多重極モーメントは、変位電流密度 j に基づいて計算できます。 PNSの超格子[26、44、45]：

ここで、 P 、 M 、 T 、 Q ^{（ e ）} および Q ^{（ m ）} それぞれ、電気双極子（ED）、磁気双極子（MD）、トロイダル双極子（TD）、電気四重極（EQ）、および磁気四重極（MQ）のモーメントです。 c は真空中の光速であり、α 、β = x 、 y 、 z 。ここで、電荷密度ρ 、通常EDおよびMQの定義に表示されますが、変位電流密度 j に置き換えられました。 \（i \ omega \ rho + \ nabla \ cdot {\ varvec {j}} =0 \）の電荷保存関係を介して。調和励振の場合〜exp（iωt ）、遠方場応答に寄与する誘導多重極モーメントの散乱力は、次のように書くことができます。

ここで、最初の2つの項は、従来のED（電荷）およびMD散乱に対応します。 3番目の項はTD散乱に対応します。 4番目と5番目の用語はEQとMQから来ています。最後の項は、高次の多重極散乱とそれらの間の結合を含む高次の項であり、通常は無視できます。式を使用することによって。 （2）–（7）、遠方場の散乱力に対するさまざまな多重極の寄与を取得できます。

図3は、Δのさまざまなシフト距離に対するPNSのさまざまな多重極の散乱力を示しています。他のパラメータは、図1cと同じです。図3a–dに示すように、Δ=0のPNSの場合、EDとMDが主要な双極子であり、対象の波長領域では共振しません。ただし、|Δ|≠0でPNSのナノホールを縮小または拡大することにより、共鳴双極子モードの励起により、デュアルバンドファノ共鳴を実現できます。観測されたデュアルバンドファノ共鳴の形成における共鳴双極子モードの重要な役割を明確に確認するために、図3e、fは、それぞれFano＃1とFano＃2の周囲にΔ=− 28nmのさまざまな多重極の正規化された散乱パワーを示しています。 。図3eに示すように、主な共振モードはFano＃1周辺のEDとTDであり、Fano＃1は電気トロイダルダイポールの共振結合の直接的な結果です。特に、EDとTDは、Fano＃1の共振チップ（918.5 nm）で同等の大きさに大幅に強化されています。したがって、EDとTDの間の破壊的な干渉により、100％の透過率を得ることができます。 Fano＃1の共鳴ディップ（916.5 nm）の場合、EDとTDの散乱が強化されるため、反射が最大化され、透過率がゼロになります。同様に、図3fに示すように、Fano＃2は磁気トロイダル双極子の共振結合から生じており、その先端（771.1 nm）はMDとTDの間の破壊的な干渉を示し、そのディップ（772.9 nm）はMDおよびTDの強化された散乱。電気トロイダル双極子または磁気トロイダル双極子の強い結合により、Δが変化しても、共振モードはFano＃1とFano＃2の両方で堅牢であることに注意してください。

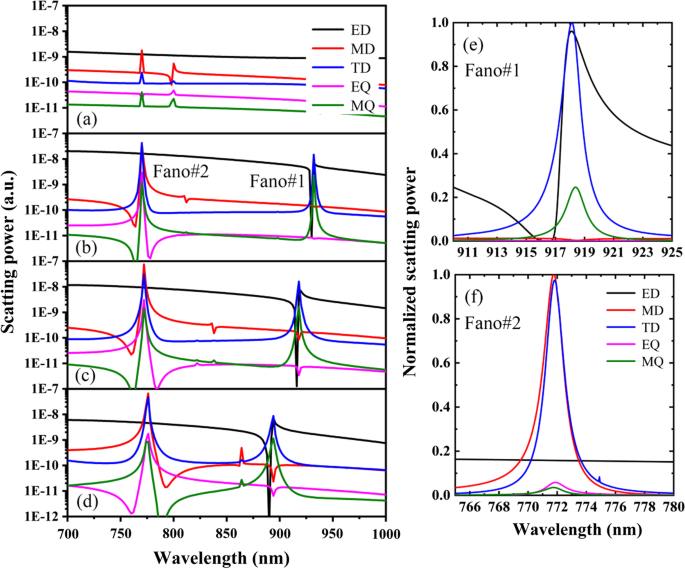
a の場合のデカルトED、MD、TD、EQ、およびMQの散乱力 Δ=0、 b Δ=− 14 nm、 c Δ=− 28nmおよび d Δ=− 42nm。 e および f それぞれFano＃1とFano＃2の周りにΔ=− 28nmの異なる多重極の正規化された散乱パワー。その他のパラメータは図1cと同じです

遠方界でのデュアルバンドファノ共鳴の伝達応答を、誘導された多重極モーメントの励起と関連付けるために、PNSの超格子のファノ共鳴の電磁場と変位電流の分布を図4に示します。図4a、b、Fano＃1の電磁界は、 x に沿った変位電流により、PNSの超格子に十分に閉じ込められています。 軸、ED共振モードを示します。さらに、Fano＃1の変位電流は、超格子の中心と端の間に2つの逆ループを形成し、磁場は yz でループを形成します。 x に沿ったTD共振モードに対応する平面 軸[44、46]。したがって、Fano＃1は、EDモードとTDモードの間の共振結合から発生します。これは、前述の多重極分解の予測結果と一致しています。実際、Fano＃1の電気トロイダルダイポールの共振機能により、Fanoの共振ピーク（918.5 nm）、中心波長（917.5 nm）、および共振ディップ（916.5 nm）での電磁界と変位電流の分布＃1は、フィールドの振幅にわずかな違いがあることを除いて、ほとんど同じです（追加ファイル1：図S1）。 Fano＃2の場合、図4cに示すように、電界が大幅に増強され、変位電流が超格子の中心とPNSの隣接する超格子の間に2つの逆ループを形成し、TD共鳴モードを示します。 z 軸。その上、Fano＃2の磁場は、 y に沿った方向で超格子に高度に局在化しています。 図4dに示すように、MD共振モードを特徴とする軸。結果として、Fano＃2は、磁気トロイダル双極子の共鳴結合の直接的な結果であり、PNSの遠方場の多重極分解の予測と一致しています。また、Fano＃2の磁気トロイダル双極子の結合により、Fano＃2の共振ピーク（771.1 nm）、中心波長（772.0 nm）、および共振ディップ（722.9 nm）での電磁界と変位電流は同様に示されます。ディストリビューション（追加ファイル1：図S2）。

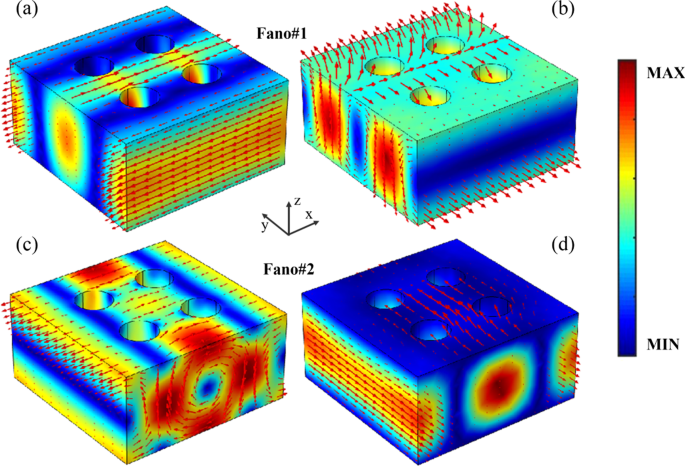
PNSの超格子のファノ共鳴の電磁界と変位電流の分布。カラーバーは電界の振幅を表し、赤い矢印は電界ベクトルまたは変位電流ベクトルを示します。その他のパラメータは図1cと同じで、Δ=− 28nmです。 a および c それぞれFano＃1とFano＃2の電界振幅と変位電流ベクトルの分布。 b および d それぞれFano＃1とFano＃2の磁場振幅と磁場ベクトルの分布

結果と考察

図5は、半径 r の関数としてのPNSの透過スペクトルを示しています。 ナノホールの値、およびその他のパラメータは図1cと同じで、Δ=− 28nmです。図5aに示すように、デュアルバンドファノ共鳴は r として維持できます。 0から最大値の67.5nmまで変化します。つまり 、四量体化された穴は超格子内で互いに接しています。ナノホール半径の増加 r PNSの表面摂動を増加させ、その実効屈折率（ERI）も減少させます。その結果、Q値が増加し、ファノ共鳴の青方偏移が発生します。具体的には、Fano＃1の共振位置は、 r の変動に対してより敏感です。 、およびデュアルバンドファノ共鳴は、四量体化された正孔が互いに近づくにつれて、1つの共鳴モードに融合する傾向があります。図5bに示すように、 r の増加 ファノ共鳴の共鳴位置をブルーシフトするだけでなく、FWHMも増加させます。 r として が25nmから45nmに増加すると、Fano＃1とFano＃2の共鳴ピークはそれぞれ936.7nmと793.2nmから887.6nmと743.8nmにブルーシフトされます。 FWHMは、それぞれ0.8nmと0.6nmから6.8nmと3.1nmに増加します。 r の増加に注意してください また、ファノ共鳴の変調度を改善し、100％の変調度を r として実現できます。 30nmより大きい。さらに、PNSの構造パラメータの影響を受けるファノピーク波長のシフトを評価することにより、ナノホール半径 r Fano＃1とFano＃2の両方で最も敏感な構造パラメータです（追加ファイル1：図S3）。したがって、 r のバリエーション PNSのデュアルバンドファノ共鳴の共鳴性能を動的に制御するための効果的なアプローチを提供します。

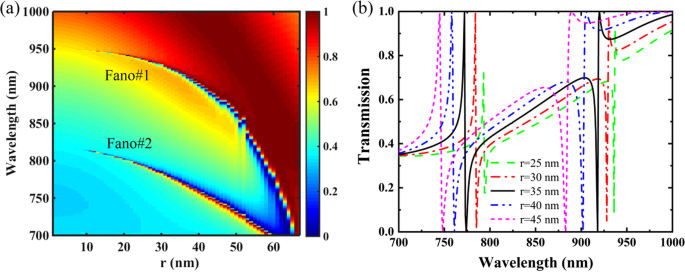
a 半径 r の関数としてのPNSの透過2Dマップ ナノホールの。 b さまざまなナノホール半径 r のPNSの透過スペクトル 。その他のパラメータは図1cと同じで、Δ=− 28 nm

図6は、PNSの伝送応答に対する構造の対称性の影響を示しています。ここで、半径 r ' 2つのナノホールの角度はゼロから互いに接するように変化し、他のパラメータは図1cと同じで、Δ=− 28nmです。図6aに示すように、 x に沿って鏡面対称の超格子の場合 軸（入射光の電界の方向）、半径 r 2つのナノホールの 'が増加し、PNSのERIの減少により、デュアルバンドファノ共鳴の共鳴位置がブルーシフトし、表面摂動の増加により、それらの帯域幅が広がります。ただし、図6bに示すように、 r を増やすと、2つのファノ共鳴を維持できます。 ′、 x に沿った超格子の鏡面対称性として、2つの追加のファノ共鳴が発生します。 軸が壊れています。一般に、 x に沿って構造の対称性を破る （ y ）軸も x に沿ったモードの対称性を破ります （ y ）周期格子の軸であり、非放射性の非縮退モードは、その縮退成分のために外部放射に結合することができます[47]。したがって、2つの追加のファノ共鳴が x に沿った鏡面対称性が破られた構造にのみ存在するという事実 軸は、それらが摂動された非縮退モードによるものであることを示しています。

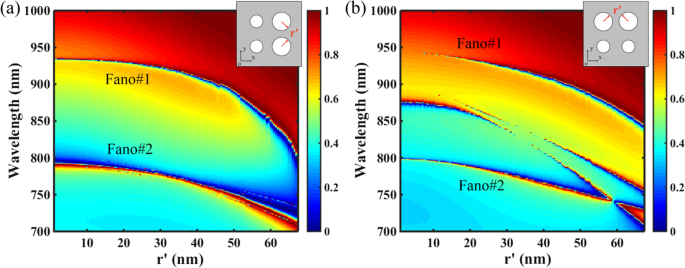
構造の対称性がPNSの伝達応答に及ぼす影響。その他のパラメータは図1cと同じで、Δ=− 28nmです。挿入図は、PNSの超格子の概略図を示しています。 a 半径 r の関数としてのPNSの透過2Dマップ x に沿った超格子の構造的対称性である2つのナノホールの ' 軸は維持されます。 b 半径 r の関数としてのPNSの透過2Dマップ x に沿った超格子の構造的対称性である2つのナノホールの ' 軸が壊れています

さらに、入射角と偏光角の影響下でのPNSの共振性能を特徴づけました。図7aに示すように、PNSのデュアルバンドファノ共鳴は、C ₄ による偏光角の変動の影響を受けません。 対称トポロジー。偏光角が0から90°、つまり x に変更されると - y への分極 -偏光、Fano＃1とFano＃2は同じに保たれます。ただし、入射角の場合、図7bに示すように、Fano＃1も入射角の変化に影響されませんが、Fano＃2は、入射角が通常の入射角から外れるとレッドシフトされ、追加のFano共鳴が発生します。 （Fano＃3）は、対称性が保護されたBICの放射減衰抑制が非垂直入射でキャンセルされたために発生します。一般に、BICのこのタイプの放射減衰抑制は、周期格子の阻止帯域の2つのエッジのいずれかで2つの逆伝播リークモードから放出された放射フィールド間の破壊的な干渉と密接に関連しています[48]。 Fano＃2とFano＃3の間の強い結合により、狭い誘導透明ウィンドウがそれらの間の近傍領域で励起される可能性があることに注意してください。

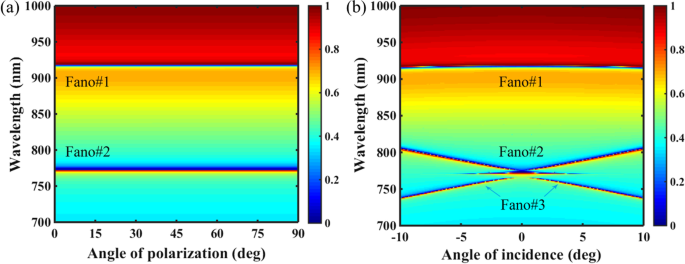
a 偏光角の関数としてのPNSの透過2Dマップ。 b 入射角の関数としてのPNSの透過2Dマップ。その他のパラメータは図1cと同じで、Δ=− 28 nm

最後に、PNSのスラブ高さHを大きくすることで、複数のファノ共鳴が得られることを示しました。図8は、非収縮（Δ=0 nm）および収縮（Δ=− 28 nm）構造のHの関数としてのPNSの透過2Dマップを示しています。図8aに示すように、Hが変化するときに、収縮していないPNSのファブリペロー（F–P）共鳴を除いて、ファノ共鳴はありません。 F–P理論によれば、収縮していないPNSのF–Pキャビティの共振条件は次のように記述できます。

ここで、δ は位相シフト、λ は自由空間の波長、 n _eff は、PNSの同等の均質スラブφのERIです。 追加フェーズであり、 m は共振次数を示す整数です。有効媒質理論[49]を使用することにより、PNSのERIは次のように推定できます。

ここで f はPNSの充填率であり、 f =1 −4π（ r /Λ） ² 。

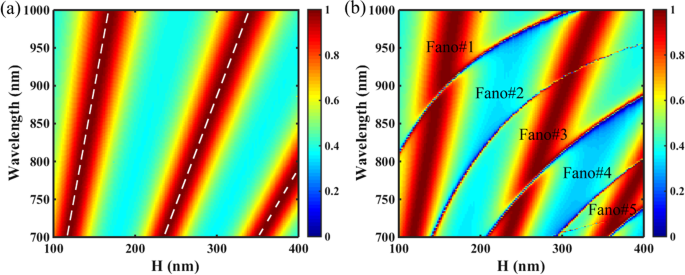
a Δ=0 nmのスラブ高さHの関数としてのPNSの透過2Dマップ。白い破線は、F–Pキャビティモデルの結果です。 b Δ=− 28nmのスラブ高さHの関数としてのPNSの透過2Dマップ。その他のパラメータは図1cと同じです

式を使用することによって。 （8）および（9）では、収縮していないPNSのF–P共鳴の位置は、λとして計算できます。 _F–P =2 π ・h・ n _eff /（mπ -φ ）。計算では、追加フェーズφ 明らかに位相シフトδに影響を与えるため、定数として扱うことはできません。 、その値は、線形フィッティング法[50、51]を使用して計算できます。図8aは、Δ=0 nmのPNSの透過2Dマップを示しており、F–P理論の結果は白い破線で示されています。図8aに示すように、F–Pキャビティモデルの白い破線はPNSの透過ピークの破線と一致しており、収縮していないPNSの透過を強化するのはF–P共振であることを確認しています。関心のあるスペクトル領域。ただし、図8bに示すように、Δ=− 24 nmの収縮したPNSの場合、Hが100〜400 nmの範囲で変化するため、Q値の高い5つのファノ共鳴が励起されてF–P共鳴と共存します。 、ファノ共鳴は非常に強いため、ファノ共鳴とF–P共鳴の間の交差領域でF–P共鳴を分割します。スラブ導波路理論によれば、フォトニック結晶スラブの厚さの増加は、構造内でより多くの漏れモードを保証します[32、52]。したがって、ファノ共鳴の数は、PNSの厚さを増やすだけで増やすことができます。四量体化された正孔のシフトはPNSのERIを変更しないことに注意してください。したがって、F–P共鳴の位置は、非収縮構造と収縮構造の両方でほぼ同じに保たれます。

結論

高Qファクターのデュアルバンドファノ共鳴は、デュアルQBICの励起に基づくPNSの比較的単純なアーキテクチャを使用することで実現できます。超格子の対角線に沿ってPNSの4つのナノホールを縮小または拡大することにより、2つの対称性保護BICをデュアルバンドファノ共鳴に変換し、それらの位置とQ値を柔軟に調整できます。 PNSのデュアルバンドファノ共鳴は、電気トロイダル双極子または磁気トロイダル双極子間の共鳴結合から生じ、超格子の遠方場多重分解と近方場分​​布の間のそれらの相関関係が検証されます。 PNSのデュアルバンドファノ共鳴は偏光に依存しない特徴を持っており、それらの高Qファクターの特徴は幾何学的パラメーターの変動に対してロバストです。 PNSの高さを増やすことにより、構造によってより多くの漏れモードをサポートできるため、高Qファクターのファノ共鳴の数を改善できます。私たちの結果は、より優れた性能を備えた高Qファクターの共振器を実現するための調整の自由度を高め、レイジング、センシング、および非線形フォトニクスの開発におけるさらなるステップを提供する可能性があります。

データと資料の可用性

現在の研究中に使用および/または分析されたデータセットは、合理的な要求に応じて対応する著者から入手できます。

略語

Qファクター：

品質係数

PNS：

平面ナノホールスラブ

BIC：

連続体の束縛状態

NIR：

近赤外線

QBIC：

準BIC

FWHM：

半値全幅

ED：

電気双極子

MD：

磁気双極子

TD：

トロイダルダイポール

EQ：

電気四重極

MQ：

磁気四重極

ERI：

実効屈折率

F–P：

ファブリペロー