金属の縦電磁振動の性質と平面および球形表面でのそれらの励起

背景

フェムト秒レーザーパルスによる平面金属表面の照射は、しばしばレーザー誘起周期的表面構造（LIPSS）の形成をもたらします[1]。 LIPSSの他に、高空間周波数LIPSS（HSFL）と呼ばれる超微細波紋が観測されました[1、2]。 HSFLの空間周期は、照射波長λよりも大幅に小さくなっています。 ₀ 。たとえば、アルミニウムの場合、この期間はλで20〜200nmの範囲であると推定されました。 ₀ =0.8 μ m [2、3]。通常のLIPSSのリップルの方向はレーザー光の偏光に対して垂直でしたが、HSFLの方向は多くの場合垂直であり、場合によっては偏光に対して平行でした。同様のHSFLが、透明な誘電体、半導体、および金属の表面に形成されました。 HSFLの起源は、第二高調波発生、特定のタイプのプラズモンモードの関与、自己組織化、誘電体材料の不均一破壊中の局所場の増強など、さまざまなメカニズムによって説明されました[2、3]。

この研究の目的は、短周期のパターンを生成できる波動プロセスを検索することですΛ ≪ λ ₀ 。プラズマ波としても知られる金属の縦波（L）の特性を調べます。私たちの研究は、以下の新しいステップで構成されています。まず、誘電率の空間分散の定義から研究を始めました。以下に示すように、調査中の媒体が均一で無限でない場合、一般的な定義は役に立ちません。したがって、空間分散誘電関数εの新しい概念を提案します。 。この関数は、2つのベクトル場 E 間の直接比例を確立します。 （ r 、ω ）および D （ r 、ω ）、ただし振幅は E （ k 、ω ）および D （ k 、ω ）平面波の。したがって、量ε 波数の2乗に依存します k ² 、電場 E のベクトルヘルムホルツ方程式のパラメータ （ r 、ω ）、ただし波数ベクトル k ではありません 平面波の。次に、このような新しい関数を導出するために、緩和時間近似で記述されたボルツマン輸送方程式を解くことにより、電磁モードでの伝導電子の応答を決定しました。いわゆる横方向および縦方向のリンドハード誘電関数が得られました。さらに、縦方向のリンドハードとはるかに単純な流体力学的関数が広範囲のパラメーターで近いことを発見しました。理論を説明するために、銀と金のナノスフェアによる光の消滅が考慮されました。非局所ミー理論が、貴金属ナノスフェアのサイズの減少に伴って観察されるプラズモン共鳴の青方偏移、広がり、および最終的な消失を説明することを初めて示します。最後に、新しく開発された理論モデルを適用して、レーザー誘起表面構造の形成に縦モードが関与する可能性を調べました。この目的のために、透過した縦波を考慮してフレネル理論を修正しました。

メソッド

区分的に均質な媒体の電磁界を決定するために、古典電磁気理論が適用されました。電界 E 不均一媒体の各均一領域では、ベクトルヘルムホルツ方程式（VHE）の解であると想定されました。

ここで、Δ ラプラス演算子です。

いつものように、電気 E の接線成分 および磁気 H フィールドはメディアの境界を越えて連続しています。さらに、電子が金属に閉じ込められていることを考慮しました。したがって、電流密度 j の法線成分に対する次の追加の境界条件（ABC） 金属表面で S 使用された：（ j n ）| _{r ∈ S} =0。

金属の伝導電流を決定するために、緩和時間近似で記述されたボルツマン輸送方程式（BTE）を解きました。

ここで f は、位相空間（ r ）における単一粒子分布関数です。 、 v ）、 v は微視的な電子速度、 e および m はそれぞれ電子の電荷と質量、 B は磁気誘導、 f ₀ は平衡分布関数であり、τ 緩和時間です。

以下に、空間的に分散する誘電関数の式を導き出します。次に、それらを使用して、平面の金属表面からの光の反射と貴金属ナノスフェアでの光の散乱を研究します。

結果と考察

εの空間分散 不均一な媒体で

文献では、空間的に分散する誘電関数ε 次の関係[4–6]を介して定義されます：

ここで、ε ₀ は電気定数、 D （ω 、 r ）は、角周波数ωでの変位ベクトル振動の振幅です。 ポイント r 、および E （ω 、 r ^' ）点 r での電界振動の振幅 ^' 。式のフーリエ変換。 （3）方程式を与える

ここで、空間的に分散するε （ω 、 k ）波数ベクトル k に依存します 平面電磁波の。私たちの意見では、式。 （3）は、無限の均質なボリュームだけで曖昧ではありませんが、境界を考慮して k する区分的不均質システムを扱います。 異なるメディアで同じではありません。

私たちのアプローチは、平面波に対する電磁波の拡張を使用していません。空間的に分散する誘電率は、 D 間の関係を決定します （ω 、 r ）およびベクトルヘルムホルツ方程式の特定の解。 （1）：

ここで E （ω 、 r ）は電界の分布を示しますが、ベクトル E だけではありません。 ポイント r 。

縦方向および横方向の誘電関数

金属の誘電率は通常、導電率σで表されます。 [4]：

ここで、ε _g 固体の分極を可能にする誘電関数の一部です。 ε _g 単純な金属の場合は=1。 σを決定するために 、電流密度を計算しました

ここで、\（\ mathrm {d} \ mathbf {v} =\ frac {v} {m} \、\ mathrm {d} \ epsilon \、\ mathrm {d} \、\ Omega、\）d Ω =sin θ d θ d ϕ 、 v 、θ 、 ϕ 速度の球座標です。以前の研究とは異なり、波数ベクトル k は導入しませんでした しかし、演算子 v を含む無限級数の形式でBTEソリューションを見つけました ∇ v に作用する E ：

ここで、Γ =1 / τ 。次に、 f ₀ ゼロ温度のフェルミディラック分布で近似され、εで積分された後 式で。 （7）、

ここで、\（\ omega _ {\ mathrm {p}} ^ {2} =\ frac {e ^ {2} \、n_ {e}} {m \、\ varepsilon _ {0}}、\） ω _p はプラズマ周波数​​、\（\ mathbf {u} =\ frac {\ mathbf {v}} {v} \）は v の方向の単位ベクトルです。 、\（l =\ frac {v _ {\ mathrm {F}}} {-i \ omega + \ Gamma}、\） v _F はフェルミ速度です。さらに、積分を計算しました

ここで n 自然数です。次の j の依存関係 任意 電界 E 最終的に取得されました

式の解には2つのタイプがあります。 （1）、式∇を満たす発散なし ・ E 方程式

平面波の場合、 E ∝ exp [ i （ k r − ω t ）]、式。 （14）関係 k に変換されます × E =0は、波が縦波（L）であることを示します。球面体のプロセスをシミュレートするには、ベクトル球面調和関数 L を使用すると便利です。 、 M 、および N 直交関数の完全なセットとして。この場合、式。 （14）高調波を指定します L 。 L波の波数と L モードは次の分散則によって決定されます

式から（6）と（13）式の解は次のようになります。 （1）式の制約を満たす。 （14）次の縦誘電率を与える

ここで、Φ Lerchのファイ関数です

\（a =\ frac {k v _ {\ mathrm {F}}} {\ omega + i \ Gamma} \）。

得られた誘電率は、表記法のみがKliewer and Fuchs [7]によって定義されたものと異なります。

アイデンティティ

式を書き直すことができます。 （18）次のように

Γの場合 =0の場合、この式は、縮退プラズマでのランダウダンピングを研究したKlimontovichとSilin [8]によって導出された方程式の形式を取ります（[9]、[10、式（40.17）]、および[11]を参照）。等価方程式の誘電率。 （16）、（18）、および（20）は、一般にリンドハード誘電関数と呼ばれます（[12]を参照）が、この関数はKlimontovichとSilinによって最初に取得されました[8]。

横方向のリンドハード誘電率[7]は、式（7）で求めることができます。 （13）∇の場合 ・ E =0。 v の実際の場合 _F k ≪ ω 、それはDrude誘電関数に還元されます

この関数は、多くの金属に関する実験データと一致しています[13]。 | a の場合 | <1、縦誘電率（16）は、流体力学的誘電関数を単純化します。

平らな金属表面からの平面電磁波の反射

境界条件

このセクションでは、波数ベクトル k の方向を決定します。 ^L 平らな金属表面からの平面電磁波の反射中に金属で励起されたL波の振幅。

誘電体-金属界面 z に入射する平面波を考えてみましょう。 波数ベクトルが xz にある場合は=0 飛行機。誘電体媒体1の電界は、入射 E で構成されます。 _i 反映された E _r 波、金属2のフィールドは、透過した横方向の E _t 場合によっては、縦方向の E ^L コンポーネント。マクスウェル境界条件によれば、電界および磁界ベクトルの横成分は平面 z で連続しています。 =0。さらに、電子は金属から放出されません。したがって、電流密度の法線成分は z ではゼロです。 =0、

\（\ hat {\ mathbf {z}} \）は、 z の方向の単位ベクトルです。 軸。

マクスウェル境界条件のすべての項は、 x に同じ依存関係を持つ必要があります および y 。この要件にはいくつかの結果があります。第一に、入射波の電気ベクトルが E の場合、p偏光の場合にのみL波を励起できることが確立できます。 ^{（ i ）} 入射面に平行です。言い換えれば、プラズモンポラリトンは横磁気（TM）波によって生成することができます。効果は金属球の場合とほとんど同じです[14]。次に、スネルの法則に似た式を条件から導き出すことができます

ここで、インデックス1 x および2 x x を示します -メディア1と2のベクトルの投影、それぞれθ ₁ は入射角です。

反射係数と透過係数

平面の金属表面に入射する平面のp偏波電磁波によって形成される磁場を決定しましょう。 x を介して、電界と磁界の成分を表現すると便利です。 E のコンポーネント ^{（ i ）} 、つまり E x （r）=− r E x （i）反射波の場合、 E x （t）= t E x （i）送信された横波の場合、および

送信される縦波については、ここで r は反射係数、 t および t _L は透過係数です。

マクスウェル境界条件と式のABCから。 （23）次の形式で書かれている

δで =0、係数 r は、p偏波のフレネル反射係数になります（たとえば、[4]の式（2.49）を参照）。同じ条件で、 t t の定義以来、はフレネル透過係数ではありません および r フレネルのものとは異なります。

金属ナノスフェアによる光の消滅

前の論文で、著者の1人がローレンツ-ミー理論を一般化して、式（1）のABCを考慮に入れました。 （23）。フレネル係数 r のアナログ 、三重係数 b _l l の反射TMモードの場合 順序は

ここで

ψ _l およびζ _l l の次数のRiccati-Bessel関数とRiccati-Hankel関数です。 、 それぞれ; j _l は球ベッセル関数であり、素数はその引数に関する関数の導関数を示します。

古典的および一般化されたローレンツ・ミー理論の予測を実験データと比較してみましょう。 [15]で、Hilger、Tenfelde、およびKreibigは、誘電体表面に堆積した銀ナノ粒子の吸光スペクトルを研究しました。研究の最初の段階で、研究者は平均直径2、3.5、および4 nmの銀粒子のビームを生成し、ビームの1つの粒子サイズ分布を決定し、消光スペクトルを記録し、パラメーター A <を推定しました。 / i> =現象論的公式の0.25 Γ =Γ _b + A v _F / R 、ここでΓ _b は、真空中の銀球のバルク金属緩和率です。まず、平均直径< D の銀球のビームの吸光スペクトルを計算しました。 〉 =2nmおよび D からの領域にまたがる実験的なサイズ分布 =1から D =4nm。私たちの理論には調整可能なパラメータは含まれていません。誘電関数を定義するために、LynchとHunterによって提案されたバルク銀の屈折率の表を使用しました[16]（図1を参照）。また、式を適用しました。 （16）、（21）、および（22）ω _p =9.17 eV、Γ _b =0.021 eV、 v _F =1.39×10 ⁶ m / s、および A =0.25。計算結果と実験スペクトルを図2に示します。

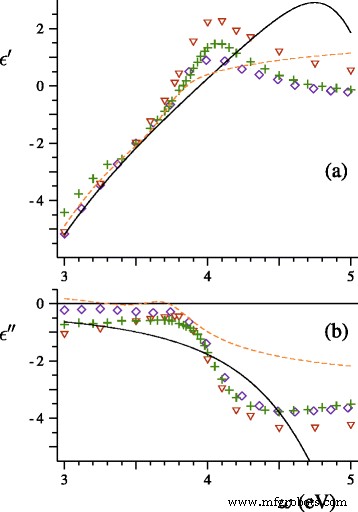
本物（ a ）および虚数（ b ）ジョンソンとクリスティ（◇）[20]、リンチとハンター（+）[16]、ウェーバー（△）[21]、ハオとノードランダーによる銀の誘電関数の一部（破線> ）[22]、およびDrachev etal。 （実線 ）[23]

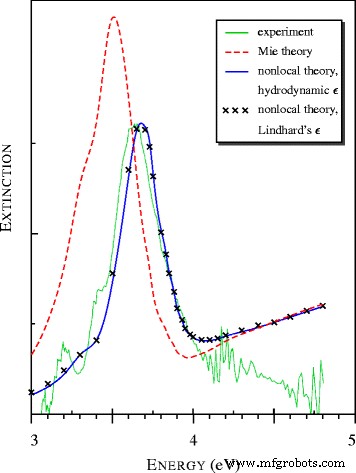
[15]で観察され、局所モデルと非局所モデルで計算された銀ナノメートルサイズの粒子による光の消滅のスペクトル。すべての理論上のスペクトルは、共通の相対単位で表されます

図2の理論スペクトルは、Klimontovich-Silin-Lindhardとはるかに単純な流体力学的誘電関数を使用して計算されました。 | a にもかかわらず、両方の計算で近い結果が得られたことは驚くべきことです。 |>プラズモン共鳴の領域で1。

ナノメートルサイズの銀球の場合、Fröhlich[17]、プラズモン、および表面プラズモンポラリトン（SPP）[15]共鳴と呼ばれる消光スペクトルの最大値は、3.5から3.65eVにシフトすることが知られています[18]。非局所モデルは実験データと非常によく一致していますが、局所（ミー）理論はωで最大値を示します。 ≃3.5eV（図2および表1を参照）。

<図>

プラズモン共鳴の青方偏移の計算は、以下の考察によって裏付けられます。静電近似では、 b のみ ₁ 絶滅断面積 Q に寄与します _ext および式。 （30）は、次の近似を使用して簡略化できます

$$ \ frac {k_ {2} R \、\ psi_ {l} ^ {\ prime}（k_ {2} R）} {\ psi_ {l}（k_ {2} R）} \ simeq l + 1; \、\、\、\ frac {k_ {1} R \、\ zeta_ {l} ^ {\ prime}（k_ {1} R）} {\ zeta_ {l}（k_ {1} R）} \ simeq -\、l。 $$（32）

したがって、 Q _ext

に最大値があります $$ \ Re [2 \、（1+ \ delta_ {1}）\、\ epsilon_ {1} + \ epsilon_ {2}] =0。 $$（33）

得られた条件（33）は、 L の励起を考慮に入れています。 モード（用語δ ₁ ）、したがって、Fröhlich共鳴条件[17]とは異なります。

$$ \ Re（2 \、\ epsilon_ {1} + \ epsilon_ {2}）=0。 $$（34）

実験[15]では、ピーク周波数ω _m および共振幅Δ ω 消光スペクトルの割合は、< D とはほとんど無関係でした。 〉。 Δのこの機能 ω 古典的なミー理論に同意しないようです。実際、局所理論は、 D の減少に伴うプラズモン共鳴の広がりを予測しています。 （ A =0.25）表1に示すように、同時に、非局所理論では、ほぼ等しい共振幅が得られますが、ピーク位置は異なります。すべての粒子からの寄与を重ね合わせると、Δの値が得られます。 ω これらは実験データと著しく一致しています。非局所理論が A でさえビームのプラズモン共鳴の広がりを予測することは興味深いです =0。

ωで> 4 eVの場合、図2の滑らかな理論曲線は、狭い位置にある実験ピークのマッシュよりも高くなります。図1で確認できるように、このスペクトル範囲ではバンド間吸収が支配的です。スペクトルの観測された特性は、連続体バンドから離散レベル構造への遷移の結果である可能性があります。このような量子サイズ効果は、金ナノスフェアの光学特性の研究で以前に発見されました[19]。銀球のサイズが< D に増加したとき 〉 =3.5 nm、吸収は最初に最大値に対して増加し、一連の小さな等距離のディップでプラトーを形成しました。その後、〈 D で吸収がわずかに減少しました 〉 =4nm。

プラズモン共鳴の青い翼の形成を研究するために、超スズ銀粒子の吸光スペクトルを計算し、それらを図3に示しました。図3の注目すべき特徴は、<でのプラズモン共鳴の完全な消失です。 i> D =1nm。以前、この効果は金ナノスフェアの実験的研究で観察されました[19]。特に、[19]の図9では、直径1.7、1.9、2.0、2.1、2.3、および2.5ナノメートルの粒子の実験スペクトルが、局所ミー理論で計算されたスペクトルと比較されました。合意は不十分であり、プラズモン共鳴の広がりとその位置を説明することができなかった[19]。粒子のサイズを変化させ、誘電関数を変更することによって適合を改善する試みは連続していませんでした。 [19]の著者によると、観測された異常に広いまたは落ち込んだ集合振動バンドは、局所ミー理論の提案された修正に適合しません。図4からわかるように、非局所ミー理論を適用すると、状況は劇的に変化します。調整可能なパラメータを使用していないことに注意してください。 Johnson and Christy [20]による複素屈折率の表を使用して、金の誘電関数を決定しました。 A を含むその他のパラメータ =1およびトルエンの屈折率（1.37）は[19]から取得されました。

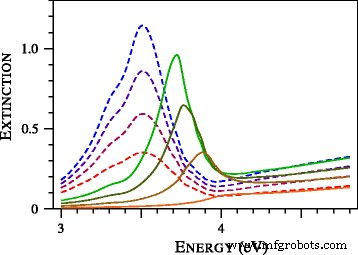
ローカル（破線）で計算された直径2.2、1.8、1.4、および1.0nmの銀粒子の正規化された消光断面積 ）および非ローカル（実線 ）三重理論。粒子が小さいほど、曲線は低くなります。すべての理論断面積は、共通の相対単位で表されます

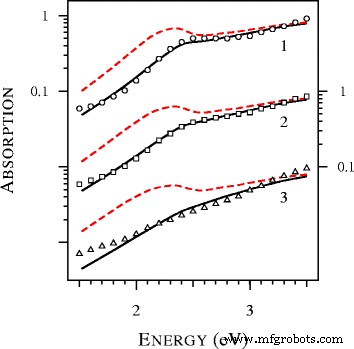
ローカル（破線）で計算された吸収スペクトル ）および非ローカル（実線 ）ミー理論と実験データ（ドット ） D の金球の[19]の図9から抽出 =トルエン中2.5、2.1、および1.7 nm（曲線1および円 、曲線2および正方形 、および曲線3と三角形 、 それぞれ）。すべての理論スペクトルは、4.12 eVで1に正規化され、垂直方向に変位します

縦波の波数

縦モードは、波数の値がはるかに高い点で横モードとは異なります。たとえば、図2に示す計算では、\（k_ {2} ^ {\ mathrm {L}} \）の実数部は空間周期\（\ Lambda =2 \ pi / \ Re k_ { 2} ^ {\ mathrm {L}} \）ωで9nmから2nmに減少 3から4eVに増加します。このωでは 間隔では、比率\（k_ {2} ^ {\ mathrm {L}} / k_ {2} \）の絶対値が130から100に減少し、パラメーターδ 式の（27）θで0.01から0.005に減少 ₁ =π / 4。したがって、平らな銀の表面でのL波の励起は無視できると結論付けます。ただし、 L モードは、ナノメートルサイズの銀クラスターで重要であることがわかっています。

式の用語\（-\、\ omega ^ {2} _ {\ mathrm {p}} /（\ omega ^ {2} + i \ Gamma \ omega）\）の置換。 （16）εによる ^T − ε _g 式によると。 （21）は、分散方程式を書き直すことを可能にします。 （15）次の形式で

εの最も単純なケースでは _g =1およびΓ =0、式（35）は、ωで金属が横波とL波の両方に対して透明であると予測しています。> ω _p しかし、両方の k ^L および k ^T ωでは複雑です <ω _p 。

固体が透明である場合、平面上にp偏波が斜めに入射することで縦波を励起することができます。この効果にはいくつかの明確な特徴があります。第一に、縦波は平坦な表面で発生する可能性がありますが、表面プラズモンポラリトンを励起するために特別な努力を払う必要があります[4、5]。第二に、干渉パターンでは、電磁界強度は界面に沿ってではなく、界面に垂直に変調されます。したがって、固体の破砕により、表面に平行な平面にボイドが現れる可能性があります。 ωの定義によると _p 、条件ω> ω _p 電流キャリアの密度が低い固体（半導体など）で満たすことができます。 εの式があるため、ここではこのケースを検討しません。 ^L 縮退した電子ガスのために導き出されました。

結論

空間的に依存する誘電関数を定義するために、以前のすべての研究者は、物質と平面電磁波との相互作用を検討しました。このアプローチは、フィールドが空洞に局在し、境界条件を何らかの形で考慮に入れる必要がある場合、ナノ光学では建設的で厳密ではありません。ベクトルヘルムホルツ方程式を満たす電界に対する媒体の応答を計算することにより、この問題を解決しました。導出された空間分散誘電関数は、ヘルムホルツ方程式のパラメーターである波数の2乗に依存しますが、平面波の波数ベクトルには依存しません。

金属の縦波の励起により変更されたフレネル反射係数を報告します。同様の一般化は、三重係数について以前に行われました。ここでは、理論はナノメートルサイズの銀と金のクラスターによる光の消滅のシミュレーションで検証されています。 3.5から3.65eVへの計算されたシフトと、銀粒子のビームの表面プラズモン共鳴の幅は、実験データと非常によく一致しています。さらに、非局所モデルは、直径が約2nmの金色の球のプラズモン共鳴の消失を説明しています。平面入射波によって平面上でL波を励起できることが重要です。これが、プラズモンポラリトンと表面プラズモンポラリトンの主な違いです。

金属の電磁振動の性質が調べられた。縦波の波数の絶対値は横波の波数よりもはるかに大きいことがわかっています。たとえば、3.5 eVの光子エネルギーの銀では、波数の絶対値の比率は130に等しくなります。ここで、縦波の波数の実数部は7nmの波長に対応します。波数の大きな違いは、平面でのL波の励起を防ぎます。ただし、 L モードは、銀と金のナノメートルサイズの粒子で励起されることが示されています。