二軸引張ひずみゲルマニウムナノワイヤの理論的研究

背景

グループIVの元素として、ゲルマニウム（Ge）はオプトエレクトロニクスとエレクトロニクスの両方で優位性を保持し、シリコン（Si）フォトニクスとの優れた互換性を備えています。 Geの本質的な特徴は、その直接バンドギャップが約0.8 eV（1.55 μ）であることです。 m）300 Kで。Geの電子と正孔の両方の移動度は、Siの移動度よりもはるかに高くなります。このように、Geは現在のSiベースの集積回路の高速デバイスで利用されてきました[1、2]。さらに興味深いことに、引張ひずみのあるGeは、上記の側面で最適化を提供します。 Geは間接バンドギャップ半導体であり、LバレーとΓの間に136meVのわずかな違いがあります。 -谷[3]。理論的には、<111> [4]に沿って一軸が約4.0％を超えるか、二軸[5、6]が約1.6〜2.0％を超えると、Γが低下する可能性があると予測されています。 -L-谷の下の谷。これにより、Geが直接バンドギャップ材料に変換され、グループIVの材料から放出される光の新しいルートが開かれます。もう1つの重要な点は、引張り歪みのあるGeが、高速相補型金属酸化物半導体デバイスを実現するためのキャリア移動度を大幅に向上させることです[7、8]。

ナノワイヤ（NW）は、表面積対体積比が大きく、キャリアと光子の両方が2次元（2D）に閉じ込められているため、魅力的な電子的および光学的特性を示します[9]。過去数年間、Si [10]またはGe / Siコア/シェルNW [11]上のGeNW（GeNW）は、Siマイクロエレクトロニクス用の金属酸化物半導体電界効果トランジスタ（MOSFET）での可能性があるため、広範囲にわたって研究されてきました。スケーリングされた相互コンダクタンスとオン電流の両方が、従来のSi p と比較して3〜4倍向上しました。 -MOSFET [12]。したがって、Si上に直接横方向GeNWをエピタキシャル成長させることで、高性能MOSFETを製造することが期待されています。張ら。 Si（001）上の極薄GeNWは、予測される表面エネルギーが最も低い{105} [13]のファセットにさらされていることに対処しました[14]。さらに、SiGe仮想基板上の歪みGe MOSFETは、正孔移動度を改善することが示されました[1]。圧縮ひずみのあるSi上の横方向のGeNWは、想定どおりにキャリア輸送の大幅な改善を示すことができますが、直接バンドギャップに変換することはできません。 GeNWに引張ひずみを導入するには、Geよりも格子定数が大きいGeSn合金[15]とIII-Sb化合物[16]が必要です。その機械的方法が一軸歪みGeNWの製造に適用されているにもかかわらず[17、18]、この製造技術の複合体は、Siベースのフォトニクスおよびエレクトロニクスにおけるモノリシック統合にはほとんど適していません。さらに、ひずみは自立型NWで簡単に解放されますが、横方向のGeNWはそれ自体で非常に高いひずみに対応できます。したがって、直接バンドギャップ遷移とキャリア移動度の向上を実現するには、2軸引張ひずみの高いエピタキシャル成長した横方向GeNWが必要です。

現在まで、InP（001）上の転位のない高二軸引張ひずみGe量子ドットは、有限要素法（FEM）によってシミュレートされた直接バンドギャップ放出の可能性を示しています[19]。これと同様に、この研究では、AlSbバッファー層を使用してSi上で直接成長させることができる緩和GaSbテンプレート上で、露出表面の形態と二軸引張ひずみGeNWの成長方向を理論的に予測します[16、20]。横方向GeNWの露出面として{110}、{105}、および{111}を選択し、定常状態システムでの総エネルギー変化を比較します。簡単にするために、この高度に歪んだシステムでは、転位と破壊の影響を無視します[21]。 FEMに基づくシミュレーションでは、臨界量のGeが存在することがわかります。臨界値を下回ると、GeNWは{105}で公開され、臨界値を超えると、{110}で公開されます。ほとんどすべてのGeNW領域は、直接バンドギャップに変換できます。これは、Γでの伝導帯の最小値と光正孔バンドの最大値の差です。 -点。また、Γでのひずみ依存キャリア有効質量の変化を定性的に分析します。 -電子と正孔の両方の移動度の向上を間接的に予測するポイント。

メソッド

横方向の北西部は通常、断面が三角形の形状を示します[22、23]。図1aに示すNWの1Dプロパティのおかげで、Zhang etal。に類似した有限NWモデル。参考文献の補足資料で。 [13]は、図1bに示すように、開始面と終了面の両方が固定されているシミュレーションに適切に使用できます。境界効果のため、北西の中央部分のみを説明し、この部分の断面は無限に長い北西の状況を表していると考えます。 FEMは、GaSbに対して7.7％の格子不整合があるGeNWの引張ひずみの分布をシミュレートするために使用されます。次の3つの状況で定常状態で同量のGeを堆積した後のシステム全体のエネルギー増分を計算します：（i）[100]成長方向（{110}ファセットが露出）（状況A）、（ii）[100]成長方向{105}ファセットが露出している（状況B）、および（iii）[110] {111}ファセットが露出している成長方向（状況C）。これら3つの状況の断面図を図1cに示します。断面積は同じに保たれ、等量のGeを表します。

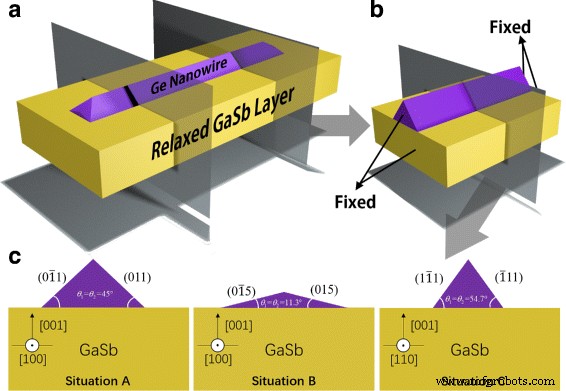
GaSbでのGeNWの概略図： a 3Dモデル、 b 簡略化された有限モデル、および c さまざまなファセットを持つGeNWの断面

単位長さ（J / nm）あたりのシステム全体のエネルギー変化には、ひずみエネルギー、表面エネルギー、およびエッジエネルギーの全体的な差が含まれ[24]、次の式で求めることができます。

第1項Δ E _{s t r a i n} Ge堆積前後の定常系のひずみエネルギー差を表し、単位体積で表されます。

結果と考察

GeとGaSbの間の7.7％の大きな格子不整合のために、システムは最初は完全な引張ひずみ下にあると考えられます。図2は、面内ひずみεを含む2D残留ひずみ分布を示しています。 _xx 、せん断ひずみε _xy 、および垂直ひずみε _zz ベース幅が w のシチュエーションAの =たとえば、緩和後の定常状態では40nmです。ここでのひずみの定義は（ a _Ges − a _Ge ）/ a _Ge 、ここで a _Ges および a _Ge それぞれ、歪んだGeと緩和したGeの格子定数です。図2aに示すように、ε _xx は、初期ひずみよりもはるかに大きい2つの基底エッジで約15.4％の最大値を持ちますが、最小値は約3.3％で、エッジから中央に向かって急激に減少します。 z で -GeNWの下部から上部への方向、ε _xx GeNWの緩和によりも低下します。 εの分布 _zz εと同様の特性を持つことがわかります _xx 図2b。 Ge薄膜の二軸ひずみとは異なり、図2cは、GeNWの非対称に分布したせん断ひずみ成分が直接バンドギャップ遷移に重要な役割を果たしていることを示しています。ひずみ分布は、3つの状況で非常に似ています。それにもかかわらず、ひずみ成分の値は、幅と高さの比率（ W ）が多様であるため、3つの状況で異なります。 / H ）その形状によって引き起こされます。 {105}面で露出したGeNWの状況Bは、最大の W を持っています / H 10の、Ge薄膜と同様の高ひずみを示します。 {111}表面が露出している状況Cは、[110]に沿った北西成長方向がひずみの不変値のままであり、εの値を上げるため、高いひずみも示します。 _xx およびε _yy 同時に。したがって、面内ひずみを緩和することはほとんどできません。

基底幅が40nmの状況AでのGeNWの残留ひずみ分布： a x成分ひずみε _xx 、 b z成分ひずみε _zz 、および c x-y平面のせん断ひずみε _xy 。下部のジグザグ形状は、部分的な基板層を示しています（以下は同じ意味です）

ひずみ分布に応じて、ひずみエネルギーの増分を求めることができます。前に説明したように、状況Bは最大のひずみエネルギー増分を保持し、状況Aは最小のひずみエネルギー増分を保持します。ただし、表面エネルギーの変化については、状況Bは断面積の増加に伴って負の値が減少し、他の2つの状況は同じ領域で非常に近い正の値を示します。エッジエネルギーの変化を除いた総エネルギー増分を図3aに示します。結果は、エネルギー増分が最低になることはないため、状況CでのみGeNWを形成する可能性が低いことを示しています。面積の増加に伴うエネルギー増加には2つの異なる結果があり、垂直の破線は面積の臨界値A _{c を示すようにマークされています。} =136.2nm ² 、これはGeの量を意味します。面積が136.2nm ² 未満の場合 、GeNWは、状況Bでは形状を形成する傾向がありますが、状況Aではより多くのGeを堆積した後です。計算結果は、GaSb上の引張ひずみGeNWが高い W を形成することを好む可能性があることを予測しています。 / H 少量のGeが堆積すると断面が三角形になり、 W は低くなります。 / H 臨界値を超えた後の1つ。図3b–eは、臨界領域の下の状況AとBにおける静水圧ひずみの分布とせん断ひずみ成分の絶対値の合計を示しています。状況AとBを比較すると、その状況にもかかわらず、Aは静水圧ひずみと| εの両方の最大値が大きくなります。 _xy | + | ε _yz | + | ε _xz |、状況Bの平均静水圧ひずみは大きくなりますが、| εの平均値は小さくなります。 _xy | + | ε _yz | + | ε _xz |。一方、状況Bは、静水圧ひずみと| εの両方の空間分布にわずかな違いがあることを示しています。 _xy | + | ε _yz | + | ε _xz |。これらの特性はGe薄膜と非常によく似ており、その高い W に起因します。 / H 価値。結果として、式を参照してください。 （5）と（6）では、状況BはΔの値が小さくなっています。 E _DT 状況Aの場合よりも、Geを直接バンドギャップ材料に変換する可能性が高くなります。

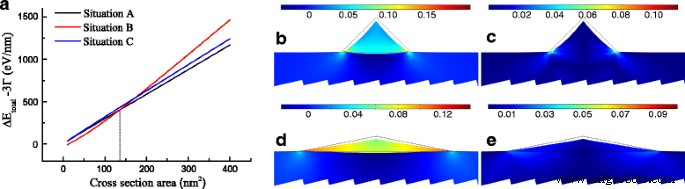
a エッジエネルギー変化を除いた総エネルギー変化3 Γ 対断面積（破線 最小値の臨界値は約136.2nm ² さまざまな状況で）。 b – e 静水圧ひずみと| ε _xy | + | ε _yz | + | ε _xz | b で 、 c 状況Aおよび d 、 e 臨界値での状況B

GeNWの引張ひずみが高いため、GeNWのほぼすべての領域を直接バンドギャップに変換できます。図4aは、Δの分布を示しています。 E _DT GeNWのサイズを大きくします。 Δの値 E _DT GeNWでは上から下にドロップします。興味深いことに、Δの最小値 E _DT は、状況Bでは断面の下端にありますが、状況Aでは下部中央にあります。この異なる分布の理由は、状況Aの下端での大きなせん断ひずみが\（\ Delta E_ {c} ^ {\ mathrm {L}} \）状況Bの場合よりも。臨界領域より下の状況BのGeNWの場合、平均Δ E _DT 図4bに示すように、臨界領域より上の状況Aの場合よりもはるかに低くなります。臨界点で、Δの平均 E _DT -0.308の値から-0.137eVに突然上昇します。さらに、同じ形状の場合、Δの分布と平均 E _DT サイズとの明らかな関係はありませんが、基本的には似ています。 GeNWのひずみとの固有の関係を発見するために、図5に基底幅のGeNWベースでの静水圧ひずみ成分をプロットします。GeNWのベースの相対位置に対するさまざまなサイズの静水圧ひずみ成分の曲線周辺領域の違いを除いて、ほぼオーバーラップしています。一貫した結果はεにあります _xx および絶対せん断成分の合計。したがって、Δのひずみ誘起値 E _DT 同じ形状のGeNWで同じ分布を持っています。

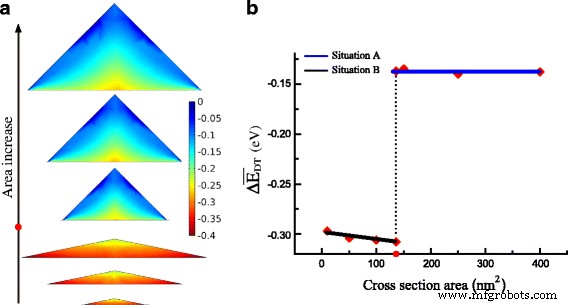
a Δの分布 E _DT 面積の増加に伴い（カラーバー Δの値を示します E _DT ）。 b Δの平均 E _DT 対エリア。臨界値は赤い点でマークされています エリア軸内

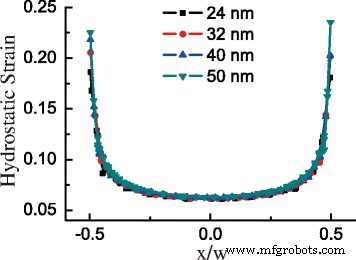
GeNWの基部の静水圧ひずみ成分と異なる基底幅のx / w

さらに、図6aに示す40nm幅のGeNWの断面におけるひずみ誘起バンドギャップマッピングをシミュレートします。バンドギャップの空間分布は、Γでのひずみ依存バンドエッジの可変値から導き出されます。 -点。図6bは、Γでのバンドエッジエネルギーを示しています。 - z に沿ってポイントします -GeNWの方向。伝導帯と価電子帯の両方のエッジ（軽いホールバンドと重いホールバンドを含む）が最初の15 nmで大幅に変化し、その後わずかに変化することがわかります。軽いホールバンドと重いホールバンドの上部は分離し、引張ひずみの増加に伴って反対方向にシフトする傾向があります。図6a、bから、バンドギャップは最初の15 nmで大幅に増加して約0.30eVに達し、その後、ほとんどのGeNW領域のバンドギャップである0.24eVの値を中心にわずかに変化します。 Γでは、軽いホールバンドの最大値が重いホールバンドの最大値よりも高いため -GeNWのポイントでは、価電子帯の正孔は、軽い正孔バンドの最大値に配置することを好みます。したがって、電子-正孔再結合は、Γで伝導帯の最小値と光正孔帯の最大値の間で発生します。 -空間に依存する電子と正孔の波動関数の重なりを無視した場合のポイント。興味深いことに、ライトホールバンドの最大値は、静水圧ひずみが約5.0％を超える、図6aで黒い曲線としてマークされた北西底の領域の伝導帯の最小値よりも上に移動します。高い引張ひずみの下で計算した負のバンドギャップは、半金属[31]や逆[32]バンド構造などの複雑な結果を引き起こす可能性があります。

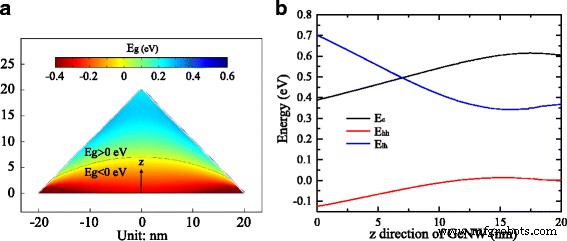
a 位置によって分布するGeNWのひずみ依存バンドギャップ。 b z に沿ったひずみ依存のバンドエッジエネルギー GeNWの方向

最後に、電子と正孔の移動度は、GeNWのこのような高張力下で強化されます。緩和されたGeの場合、電子輸送は主にLバレーに存在する電子によってもたらされます。 Geに引張ひずみがあり、Γ -谷は図3aに示すようにL谷の下にあり、電子伝達の主な寄与はΓからです。 -谷。一方、輸送における正孔の主な関与は、Γの軽いホールバンドからのものです。 -高い引張ひずみ下の点。一方、緩和された場合、重いホールバンドが価電子帯の最大値を占めます。 Γでの電子の有効質量がはるかに小さいため -L点よりもポイントが大きく、有効質量が重いホールバンドの最大値から軽いホールバンドの最大値に減少することで、電子だけでなく正孔の移動度も向上します。引張ひずみは、Γでの電子と正孔の有効質量を減少させると理論的に予測できます。 - Califano による量子ドットのモデル内の点 およびハリソン [29]。定量的な計算方法はNWモデルには適していませんが、引張ひずみが k での有効質量を変更する可能性があると定性的に想定しています。 小さい k の分散関係の曲率を大きくすることで=0 Γの近く -点。したがって、電子と正孔の両方の移動度は、引張ひずみのあるGeNWで強化できます。分裂する価電子帯はまた、強い電子-フォノン結合とバンド内散乱を誘発し[33]、これにより正孔移動度が電子移動度よりも低くなるように制限されます。

結論

要約すると、GaSb上の引張ひずみGeNWを提案し、Ge堆積前後の総エネルギー変化を介して3つの異なる状況を比較しました。結果は、GeNWが臨界量の前に〈100〉成長方向に沿って{105}表面を形成する傾向がある一方で、臨界量の後に{110}表面によって露出されることを示しています。残留ひずみ場とバンドギャップ分析は、同じ形状がひずみとΔの両方で同様の分布を持っていることを示しています。 E _DT サイズに関係なく。さらに、面内ひずみと静水圧ひずみは、すべての状況で、端から中央だけでなく、下から上にも減少します。引張ひずみが高いため、GaSb上のGeNWのほぼ全体が、2つの可能な状況で直接バンドギャップ材料に変換されます。また、光正孔は主にΓでの電子正孔再結合と電気輸送に関与します。 -光の穴のバンドの最大値が高張力ひずみの価電子帯の最大値になるため、ポイント。 Γでのキャリア有効質量の減少により、電子だけでなく正孔の移動度も向上させることができます。 -引張ひずみによって決定される点。理論的に予測される魅力的な性能は、引張り歪みのあるGeNWが、光源用のオプトエレクトロニクスと、Siフォトニクスとエレクトロニクスの高速デバイス用のマイクロエレクトロニクスにそれぞれ適用される可能性があることを意味します。