周期的ポテンシャルの下でのシリセンのスピンおよび谷に依存する電子構造

背景

シリセン[1、2]、遷移金属ジカルコゲナイド[3、4]、フォスフォレン[5]などのグラフェンが発見されて以来、六角形の格子構造を持つ2次元（2D）ディラック材料が広く研究されています。グラフェンには多くの特定の特性がありますが、その用途はゼロバンドギャップと弱いスピン軌道相互作用（SOI）によって制限されます。最近、グラフェンのシリコン類似体であるシリセンがエピタキシャル成長によって製造され[6–10]、その安定性は理論的研究によって予測されています[11、12]。グラフェンとシリセンは、 K の周りに類似したバンド構造を持っています および K ^' 谷、および両方の低エネルギースペクトルは、相対論的ディラック方程式[13]によって記述されます。グラフェンとは異なり、シリセンは強い固有のSOIと座屈した構造を持っています。強力なSOIは、ディラック点[13、14]でギャップを開き、スピンと谷の自由度の間の結合につながる可能性があります。座屈した構造により、シリセンシートに垂直な外部電場によってバンドギャップを制御することができます[14–16]。さらに、シリセンには、既存のシリコンベースの電子技術との互換性が高いという利点があります。これらの特性により、シリセンは次世代のナノエレクトロニクスにとって優れた材料になっています。特に、室温でのシリセン電界効果トランジスタは、実験[17]の成長移動製造プロセスによって首尾よく製造されました。

2D Dirac材料の発見は、谷の量子制御を探求する新しい機会を提供します。 2つの同等でない谷 K および K ^' 最初のブリルアンゾーンでは、量子情報と量子計算のための電荷とスピンに加えて、追加の自由度と見なすことができます[18–20]。たとえば、谷の自由度を組み込んで、電子スピン量子ビットをスピン谷量子ビットに拡張することができます[18]。したがって、谷の疑似スピンを生成、検出、および操作することを目的とするvalleytronicsはかなりの関心を集めています。グラフェンでは、独自のエッジモード[21、22]、三角ワーピング効果[23]、トポロジカルライン欠陥[24、25]、ひずみ[26、27]、および静電ゲートを利用して、谷分極を実現するさまざまなスキームが提案されています。 [28]。グラフェンと比較して、シリセンは谷の疑似スピンの研究において大きな利点があります。シリセンは、さまざまな外部場の変調の下で、多種多様なトポロジカル相とチャーン数を示すことがわかっています[13、16、29、30]。電界の存在下で E _z および交換フィールド h 、江沢は E の状態図を調べました _z − h スピンと谷のインデックスによって特徴付けられる平面[16]。さらにラシュバSOIを考慮すると、トポロジカルな相転移により、シリセンでは谷分極量子異常ホール状態が予測されます[31]。状態遷移に基づいて、弱い無秩序に対してロバストな、ほぼ100％のスピン偏極を備えたシリセンベースのスピンフィルターが提案されています[32]。横山は、強磁性（FM）シリセン接合を通る弾道輸送を研究し、制御可能なスピンと谷の分極電流を示しました[33]。反転対称性が壊れた遷移金属ジカルコゲナイドでは、時間反転対称性のために、固有のSOIから生じる価電子帯のスピン分裂が2つの谷で反対になります[3、34、35]。反転対称性が壊れていると、谷に依存する光学選択規則が生じる可能性があります。これを使用して、 K のキャリアを選択的に励起できます。 または K ^' それぞれ右または左の円偏光を介した谷[3、34]。実験では、谷の偏光の信号は、光学的[36、37]および輸送[38、39]測定によって精査されました。対称性を破るゲート電場にさらされた二層グラフェンで巨大な非局所的谷ホール効果が観察され、非局所的信号は室温まで持続します[38]。 2D Dirac材料のvalleytronicsの最近のレビューは、参考文献に記載されています。 [40]。

超格子は、半導体や2D材料の電子構造を設計する効果的な方法です[41]。グラフェンまたはシリセンを金属基板の上に配置すると、実験でナノスケールの超格子パターンが自然に発生する可能性があります[42、43]。グラフェンの超格子は、実験的に観察された[43、48、49]キラルな性質により、異方性フェルミ速度の繰り込み[44]と、スペクトル内の新しいディラック点の生成[45–47]につながる可能性があります。電場を伴うシリセン超格子 E _z および交換フィールド h 、スピンとバレーの両方の縮退が解除されます。超格子によって引き起こされるミニバンド構造とミニギャップは、スピンと谷の指数に依存することが確認されています[50]。さらに、スピンと谷の分極は、シリセン超格子によって強化される可能性があります[51]。グラフェンと同様に、シリセン超格子には多くの新しい電子構造が期待されています。しかし、シリセン超格子に関する研究は非常に少ない[50,51]。この論文では、補足的な側面、すなわち、スピンおよび谷に依存するバンド構造とシリセンの輸送特性について詳細に説明します。スピン指数と谷指数は、構造パラメーターによって調整できる追加のディラック点と異方性速度に異なる影響を与えることがわかりました。電界と交換電界により、速度が大幅に抑制されます。顕著なスピンと谷の分極が達成され、これは無秩序によって大幅に強化される可能性があります。

この論文は次のように構成されています。 「方法」のセクションでは、理論的な形式と分散関係を示します。バンド構造、スピンおよび谷偏光透過率の数値結果は、「結果と考察」のセクションに示されています。最後に、「結論」セクションの要約で締めくくります。

メソッド

単一粒子近似では、ディラック点の近くのシリセンの電子構造は、効果的なディラックハミルトニアンに従います。検討中のシステムは、一連の局所的なポテンシャル障壁 U によって形成された一次元シリセン超格子です。 、フィールドを交換する h 、および垂直電界 E _z 。 U 、 h 、および E _z バリア幅が d のバリア領域にのみ存在します _b 、一方、 U = h = E _z ウェル幅 d のウェル領域では=0 _w 、図1に示すように、クロニッヒペニー型の超格子は x に沿ってのみ変化します。 方向、および1ユニットの長さは d = d _b + d _w 。同様のモデルがRefsで説明されています。 [51、52]、これは、この研究で研究されたバンド構造と無秩序効果ではなく、主に熱電および電子輸送に焦点を当てています。実験的に、 U 金属製のゲートと h によって生成できます シリセン層の上に周期的に堆積するFM絶縁体EuO [33]による磁気近接効果によって生成できます（図1を参照）。電界 E _z シリセンに垂直に適用すると、千鳥状の副格子電位を誘発する可能性がありますΔ _z =ℓ E _z 、2 ℓ A の垂直方向の間隔は約0.46Å および B 座屈構造による2つの副格子の部位[16]。したがって、電子状態はハミルトニアンによって記述できます。

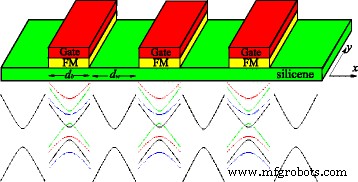
上：シリセン超格子の概略図。シリセンの上部にあるEuOやEuSなどのFM絶縁体は、グラフェンで提案されているように、シリセンの交換場を誘導します[53]。 FM絶縁体の上部にある金属ゲートは、フェルミ準位を局所的に制御します。下：外部場がある場合とない場合のシリセンのエネルギースペクトルの概略図

Δ _{η σ} =Δ _z − η σ λ _SO さまざまなスピンおよび谷のインデックスのバンドギャップについて説明します。これは、千鳥配置のポテンシャルΔによって制御できます。 _z およびSOI λ _SO 。 U _σ = U − σ h さまざまなスピン指数の有効ポテンシャルです。 η =±1は K を示します および K ^' 谷。 σ =±1はスピンアップとスピンダウンの状態を示します。 v _F はフェルミ速度です。シリセンでは、内因性および外因性のラシュバ効果は非常に小さく、無視することができます[15]。

y に沿った並進不変性のため 方向、横波ベクトル k _y 保存されています。谷の波動関数η σをスピンします 各地域の形式はΨです。 （ x 、 y ）=ψ （ x ） e ^iky _y

バリア領域では、ε _{η σ} =ε _b =（ E − U _σ ）+ Δ _{η σ} および x 波数ベクトルの成分\（q _ {\ eta \ sigma} =q_ {b} =\ sqrt {（E --U _ {\ sigma}）^ {2}-\ Delta ^ {2} _ {\ eta \ sigma} -（\ hbar v_ {F} k_ {y}）^ {2}} / \ hbar v_ {F} \）。井戸地域では、ε _{η σ} =ε _w = E − η σ λ _SO および\（q _ {\ eta \ sigma} =q_ {w} =\ sqrt {E ^ {2}-\ lambda _ {SO} ^ {2}-（\ hbar v_ {F} k_ {y}）^ { 2}} / \ hbar v_ {F} \）。 k _± = q _{η σ} ± i η k _y 。送信確率 T _{η σ} 伝達行列手法を使用して計算できます。ゼロ温度での特定の谷の特定のスピンの正規化されたコンダクタンスは、

ここで、θ x に対する入射角です。 方向。スピンおよび谷分解コンダクタンスは、\（G _ {\ uparrow（\ downarrow）} =\ left（G_ {K \ uparrow（\ downarrow）} + G_ {K ^ {\ prime} \ uparrow（\ downarrow）として定義されます。 ）} \ right）/ 2 \）および\（G_ {K（K ^ {\ prime}）} =\ left（G_ {K（K ^ {\ prime}）\ uparrow} + G_ {K（K ^ { \ prime}）\ downarrow} \ right）/ 2 \）、それぞれ。次に、スピン偏極 P を紹介します。 _s 谷の偏光 P _v ：

ブロッホの定理と波動関数の連続条件に基づいて、分散関係 E （ k _x ） K 付近のスピンアップおよびスピンダウン電子の場合 および K ^' 谷は計算できます、

および k _x ブロッホ波数です。計算を単純化するために、無次元単位が導入されています：\（E \ rightarrow E d / \ hbar v_ {F} \）、\（U \ rightarrow U d / \ hbar v_ {F} \）、\（\ lambda _ {SO} \ rightarrow \ lambda _ {SO} d / \ hbar v_ {F} \）、\（\ Delta _ {z} \ rightarrow \ Delta _ {z} d / \ hbar v_ {F} \） 、\（h \ rightarrow hd / \ hbar v_ {F} \）、 k _y → k _y d 、 k _x → k _x d 、 d _w → d _w / d 、および d _b → d _b / d 。 Δで注意してください _z =λ _SO = h =0、式（6）は、周期的ポテンシャルのギャップレスグラフェンで見られるものに還元され、スピンと谷の両方が縮退します[44–47]。式から（6）、その交換フィールド h を見ることができます 谷が縮退を維持している間、単独でスピンの分裂を引き起こす可能性があります。ただし、谷の縮退は電界 E によって解除できます。 _z SOI λの助けを借りて _SO 。したがって、交換場と電場の組み合わせは、図1に示すように、スピンと谷の縮退を持ち上げることができます[16、31–33]。提案されたシステムでは、異なる谷の近くで異なるスピンを持つ電子はさまざまなバンドを示します構造と輸送機能。

結果と考察

このセクションでは、上記の方程式を使用して、シリセン超格子のさまざまなスピンおよび谷指数のバンド構造と輸送特性を計算します。以下では、バリアとウェルの幅は同じであると想定されています。ウェルとバリア幅が等しくない場合の結果（ d _b ≠ d _w ）はギャップレスグラフェン[47]のものと似ています。一部のパラメータは d として設定されます _b = d _w =50nmおよびλ _SO 特に明記しない限り、シリセンで=3.9meV。フェルミ準位近くの最初の2つのミニバンド（最低の価電子帯と伝導帯のミニバンド）に集中します。

スピンおよびバレーに依存するバンド構造

まず、潜在的な U の影響 ミニバンドの場合を図2に示します。エネルギーバンドのギャップのあるケースとギャップのないケースを同時に説明するために、Δを設定します。 _z =7.8 meV =2 λ _SO 。可能性がない場合（ U =0）、 K 付近のスピンアップ電子 谷（ K ↑ 電子）および K 付近のスピンダウン電子 ^' 谷（ K ^' ↓ 電子）はギャップレスですが（図2（a1、a4）を参照）、 K 付近のスピンダウン電子 谷（ K ↓ 電子）および K 付近のスピンアップ電子 ^' 谷（ K ^' ↑ 電子）には大きなギャップがあります（図2（a2、a3）を参照）。スピンアップ（またはスピンダウン）電子のミニバンドは、 E から負（または正）のエネルギー範囲にシフトします。 =0 by h 、有効ポテンシャル U による _σ = U − σ h 。 K のバンド構造 ↑ （または K ↓ ）電子と K ^' ↓ （または K ^' ↑ ） E に関して電子が鏡面対称である =0、式と一致します。 （6）。ただし、この鏡面対称性は U の存在下で破壊されます 。明らかに、 U として 増加すると、余分なディラックポイントが表示され、その間にその数が増加します。余分なディラック点は、それらの近くの波動関数のキラリティーによって示されます[46]。図2に示すように、シリセンシステムのディラックポイントの機能は、スピンと谷の自由度に大きく依存しています。たとえば、 U = K の場合、図2（d1〜d4）の135 meV ↑ 、 K ↓ 、 K ^' ↑ および K ^' ↓ 電子の場合、ディラック点の数はそれぞれ5、6、4、7です。 U の特定の値について 、 U など = K の場合は40.66meV ↓ 電子（図2（b2）を参照）および U = K の場合は100.63meV ^' ↑ 電子（図2（c3）を参照）では、 k で新しいディラック点を生成できます。 _y =0であり、 k から反対方向に移動するペアに分割されます _y =0ポイントですが、常に k を維持します _x =0、 U として さらに増加し​​ます。結果として、 K のバンドギャップ ↓ および K ^' ↑ 電子は閉じられ（図2（b2、c3）を参照）、ギャップのあるシステムはギャップがなくなります。 U の臨界値を見つけるために 、 d を設定します _b = d _w および k _x =0。陰関数定理を考慮に入れると、ギャップレスグラフェンの規則[47]と同様に、新しいディラック点での縦波数ベクトルは q を満たすと結論付けることができます。 _b = q _w

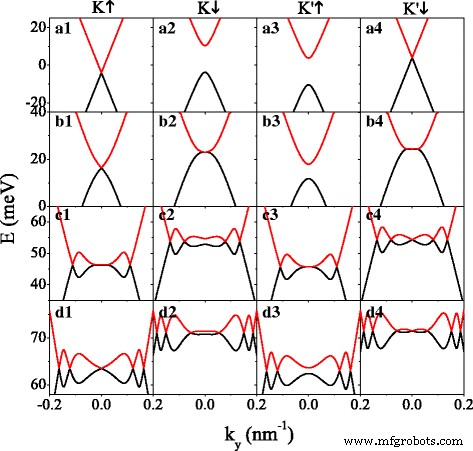
エネルギースペクトルと k _y 潜在的な U のいくつかの異なる値 。 （a1–a4） U =0; （b1–b4） U =40.66 meV; （c1–c4） U =100.63 meV; （d1–d4） U =135.0meV。パラメータの値は h です。 =8.0 meV、Δ _z =7.8 meV、および k _x =0

K の場合 ↑ および K ^' ↓ ηの電子 σ =1、Δの場合 _z =2 λ _SO 、式（7）に減らすことができます

同様に、式。 （6）は

これは、\（\ left（\ epsilon _ {b} ^ {2} + \ epsilon _ {w} ^ {2} \ right）q_ {w} ^ {2} +（\ epsilon _ {b}- \ epsilon _ {w}）^ {2} k ^ {2} _ {y} =-2 \ epsilon _ {w} \ epsilon _ {b} q_ {w} ^ {2} \）または q _w d =2 n π （ n は正の整数です）。式に基づく。 （8）、εがあります _b =− ε _w 、したがって、前者の等式は、 k の場合にのみ満たされます。 _{y 0} K の場合は=0 ↑ および K ^' ↓ Δの電子 _z =2 λ _SO 、元のディラックポイントに対応します。 q のソリューション _w d =2 n π フォームを持っている

\（\ sqrt {E_ {0} ^ {2}-\ lambda _ {SO} ^ {2}} d / 2 \ pi \ hbar v_ {F} \ geq n \）の場合、 k > _{y 0} は本物であり、（ E に正確に配置された新しいディラックポイントが発生します ₀ 、 k _{y 0} ）。 U の値が低い場合 、 k _{y 0} は虚数であり、 n の解決策はありません 、これは余分なディラックポイントがないことを意味します。ディラックポイントは、 U の臨界値の後にのみ表示されます 、 U など = K の場合は40.66meV ↓ n に対応する図2（b2）の電子 =1。式によると。 （10）、ディラックポイントの数 N _D 取得できる。 Δの場合 _z =2 λ _SO 、

K の場合 ↑ および K ^' ↓ 電子、

K の場合 ↓ および K ^' ↑ 電子。ここで、[...]は整数部分を示します。 U の臨界値で注意してください 、 U など =40.66meVおよび100.63meV、ディラックポイントの数は N _D =2 n K の場合は-1 ↓ および K ^' ↑ 電子（図2（b2、c3）を参照）。

式（7）と（10）は、ディラック点の位置と数が電界 E によって調整できることを示しています。 _z および交換フィールド h 。図3は、ディラックポイントの数を示しています N _D U の関数として E のさまざまな値の場合 _z および h 。 Δの場合 _z =7.8 meV（図3a）、 U の増加 、 N _D K の場合 ↑ および K ^' ↓ 電子は奇数の形で増加し、式（1）と一致します。 （11）。 N _D K の場合 ↓ および K ^' ↑ 電子は偶数の形で増加し、式（1）と一致します。 （12） N を除く _D 臨界値で。図3aとbを比較すると、 h 増加すると、スピンダウン（またはスピンアップ）電子の臨界値は徐々に減少（または増加）します。 Δの場合 _z =15meV≠2 λ _SO 図3cでは、 N _D N を除いて、すべての電子は偶数の形で増加します _D 臨界値で。明確に、 U の臨界値 スピンと谷が異なる電子では異なります。ディラックポイントは、パラメータ U の共同変調によって制御できます。 、 E _z 、および h 。

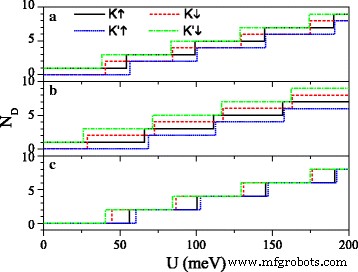
ディラックポイントの数 N _D 対潜在的な U 。 （ a ） h =8.0meVおよびΔ _z =7.8 meV; （ b ） h =20.0meVおよびΔ _z =7.8 meV; （ c ） h =8.0meVおよびΔ _z =15.0 meV

潜在的な U およびバリア幅 d _b 図4に示すように、バンドギャップを調整するために使用できます。 K のギャップ ↑ および K ^' ↓ 電子は小さいが、 K のギャップは小さい ↓ および K ^' ↑ Δのために電子が大きい _{η σ} =Δ _z − η σ λ _SO 。 U として 増加すると、すべてのミニバンドが徐々に高エネルギー領域に向かって移動し（図4aを参照）、すべてのバンドギャップが U で減衰振動を示します。 （図4bを参照）。 U の場合 =σ h 、実効電位はゼロで、ギャップは最大値に達します。ギャップは U の臨界値で閉じられます 、新しいディラックポイントの出現のため。図4c、dは、ミニバンドとバンドギャップのバリア幅への依存性を示しています d _b U で =0。外部フィールドがない場合（ d _b =0）、ミニバンドは縮退し続け、フェルミ準位でのギャップは2 λです。 _SO 。 d の外観で _b 、ミニバンドは分割され、谷とスピンは縮退しなくなります。 K のミニバンド ↑ （または K ↓ ）および K ^' ↓ （または K ^' ↑ ）電子は E について鏡面対称を保ちます =0（図4cを参照）。 d として _b 増加すると、 K のギャップが増加します ↓ および K ^' ↑ 電子は徐々に広がります。 K のギャップ ↑ および K ^' ↓ d のとき、電子はゼロに減少します _b d を満たす _b / d _w =λ _SO / Δ _z 、その後 d で増加します _b （図4dを参照）。 d がさらに増加すると、ギャップ幅は飽和状態に近づきます。 _b 。さらに、ミニバンドの幅は d として狭くなります _b 固有状態の結合が少ないため、増加します（図には示されていません）。バンドギャップに対する電界の影響は、以前の研究[50]の影響と類似しています。

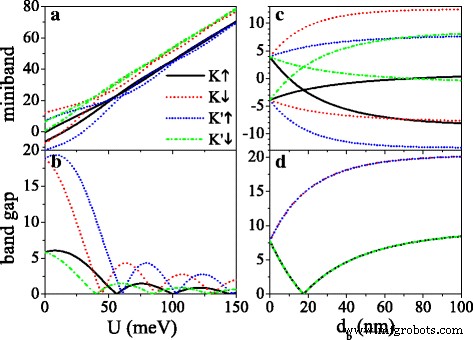
（ a ）フェルミ準位と（ b の近くのミニバンド ）元のディラック点と潜在的な U でのバンドギャップ 、 d で _b = d _w =50nm。 （ c ）フェルミ準位と（ d の近くのミニバンド ）元のディラック点と d でのバンドギャップ _b 、 U で =0および d _w =50nm。他のパラメータの値は h です =8.0 meV、Δ _z =15.0 meV、および k _x = k _y =0

群速度は、図5に示すように、スピンと谷のインデックスに強く依存します。成分（ v _x 、 v _y ）の速度は

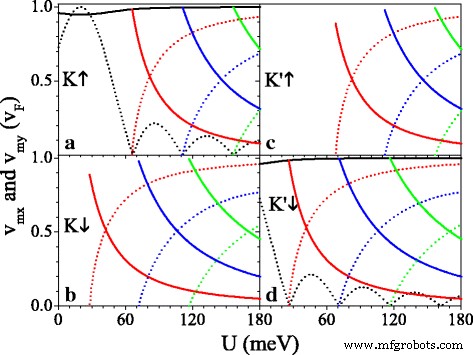
（ a – d ）速度と潜在的な U 、およびパラメータは h として設定されます =20.0meVおよびΔ _z =7.8meV。黒、赤、青、緑の実線の曲線は速度 v _{0 x} 、 v _{1 x} 、 v _{2 x} 、および v _{3 x} 、 それぞれ。黒、赤、青、および緑の破線の曲線は、速度 v です。 _{0 y} 、 v _{1 y} 、 v _{2 y} 、および v _{3 y} 、それぞれ

図5は、速度成分 v を示しています。 _mx および v _私の v の単位 _F 元のディラックポイントで（ m =0）および新しいディラックポイント（ m =1,2,3）。 U としてそれを見ることができます 増加、 v _{0 y} 減衰して振動し、 v _{0 x} ≈ v _F 影響はほとんどありません（図5a、dを参照）。 U の臨界値で 新しいディラックポイントが出現する場所、 v _mx ≈ v _F しかし v _{0 y} = v _私の =0、 k に沿ったコリメーション動作を示します _x 特定のスピンと谷の方向。 U の場合 臨界値を超えてさらに増加し​​、 v _私の v に増やします _F しかし v _mx 徐々にゼロに減少します。周期的ポテンシャルの効果は、キラルな性質の結果として、非常に異方性があります。異方性速度の特徴は、ギャップΔにより、スピンや谷によって異なります。 _{η σ} そして潜在的な U _σ 、 U を使用してコマンドを実行できます 。 U を取る =20 meV、たとえば v _{0 y} = v _F K の場合 ↑ 電子は v よりはるかに大きい _{0 y} =0.16 v _F K の場合 ^' ↓ 電子であり、 v はありません _{0 y} K の場合 ↓ および K ^' ↑ バンドギャップによる電子。 v _mx （または v _私の ）スピンアップ電子の場合は、同じ谷のスピンダウン電子の場合よりも常に大きい（または小さい）。特に、図5は、 U の値が小さい場合も意味します。 、 v _{0 x} 、 v _{0 y} 、および v _mx v 未満です _F Δによる _z および h 、ギャップレスシステム以外[44]。たとえば、 v _{1 x} =0.98 v _F 、0.89 v _F 、0.89 v _F 、および0.98 v _F K の場合 ↑ 、 K ↓ 、 K ^' ↑ および K ^' ↓ それぞれ、ディラック点が現れるときの電子。 Δの影響を明らかにするために _z および h 群速度については、図6に速度（ v ）を示します。 _{0 x} 、 v _{0 y} ）（a）Δの関数として _z および（b） h K の場合 ↑ 電子。図6aから、 v であることがはっきりとわかります。 _{0 x} Δで単調に減少します _z v _{0 y} Δの変化に鈍感です _z 。それどころか、 v _{0 x} h に対して鈍感です 、 v _{0 y} 最大値に増加 v _{0 y} = v _F h で =σ U その後、 h で減少します 。結果は、群速度がΔによって抑制できることを示しています。 _z および h シリセンで。

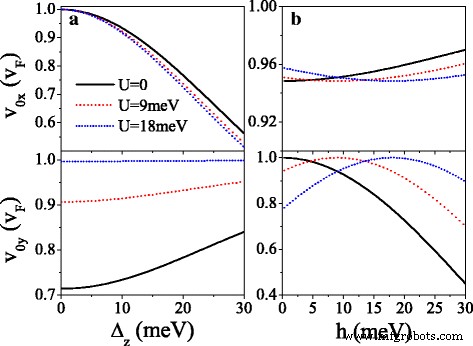
速度 v _{0 x} および v _{0 y} 対（ a ）Δ _z および（ b ） h 、 K の場合 ↑ 電子。 （ a ） h =20.0meVおよびλ _SO =Δ _z / 2。 （ b ）Δ _z =7.8 meV

スピンおよびバレー偏光トランスポート

スピンと谷に依存するバンド構造は輸送特性に反映され、輸送を制御するためのガイドを提供します。このセクションでは、有限のシリセン超格子を通るスピン分極および谷分極輸送の特性について説明します。図7は、伝送確率 T を示しています。 _{η σ} （a、c） K の場合 ↑ および（b、d） K ↓ 電子、および周期番号 n =10。赤い破線の曲線はミニバンドであり、送信を決定するさまざまな電子状態の境界でもあります。ミニバンド領域では送信が制限されており、バンドギャップ領域では送信が制限されていないことがわかります（図7a、bを参照）。透過率の分布は k を中心に対称です _y 対称ミニバンドのため=0。伝送の共振特性は、共振状態から生じます。トランスミッションは k の近くのギャップ領域にまだ存在することに注意してください。 _y 固有状態のトンネル効果のために=0。 T _{η σ} K のフェルミ準位 ↑ および K ↓ 電子はそれぞれ図7c、d）に示されています。 T の多くの薄い共振ピークがはっきりとわかります。 _{η σ} =1はディラック点の位置で正確に発生し、スピンと谷のフィルターとしてのシステムの適用を示唆しています。

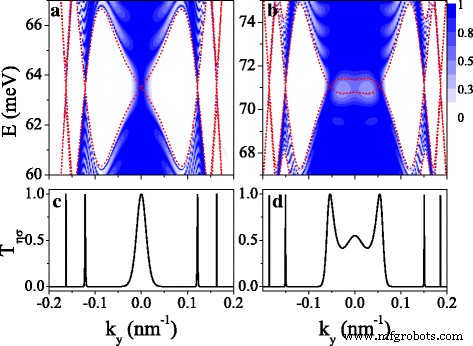
トランスミッションの等高線図 T _{η σ} （ E 、 k _y ）for（ a ）、（ c ） K ↑ 電子と（ b ）、（ d ） K ↓ 電子。パラメータの値は、図2（d1〜d4）の値と同じであり、 n =10

スピンと谷のインデックスへのバンド構造の強い依存性は、高いスピンと谷の分極の実現に有益です。図8は、ミニバンド、コンダクタンス G を示しています。 _{η σ} 、スピン偏極 P _s 、および谷の分極 P _v 潜在的な U の関数として 。コンダクタンスの分布はバンド構造と完全に一致していることがわかります。つまり、コンダクタンス（またはコンダクタンスギャップ）はミニバンド（またはバンドギャップ）に対応します。スピンアップ電子とスピンダウン電子のミニバンドは、 h を調整することで代替分布にすることができます。 ちゃんと。したがって、\（G_ {K（K ^ {\ prime}）\ uparrow} \）と\（G_ {K（K ^ {\ prime}）\ downarrow} \）は、代替分布、つまり\（G_ {K（K ^ {\ prime}）\ uparrow} \）は、\（G_ {K（K ^ {\ prime}）\ downarrow} \）が共鳴している領域ではほとんど消え、その逆も同様です。この結果は、顕著なスピン偏極に直接つながり、スピン偏極のスイッチング効果を提案します（図8aを参照）。 Δを変更する _z 、 K 付近の電子のミニバンドとコンダクタンス および K ^' 谷を制御して、完全に谷に分極した電流を発生させることができます（図8bを参照）。スピン偏極と比較して、谷分極は十分に完全ではありません。ただし、この欠点は、以下で説明するように、システムの無秩序構造によって改善できます。

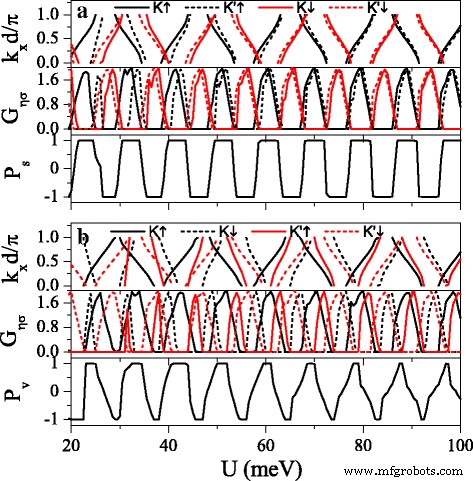
ミニバンド、コンダクタンス G _{η σ} 、スピン偏極 P _s 、および谷の分極 P _v 対潜在的な U 。 （ a ）Δ _z =4.0meV。 （ b ）Δ _z =12.0meV。その他のパラメータは h として設定されます =7.0 meV、 E =6.0 meV、 d _b = d _w =120 nm、および n =10

図9は、（a）スピン偏極 P を示しています。 _s （b）谷の分極 P _v in（ U 、 h ） 空。興味深いことに、両方の P _s および P _v 強磁性シリセン接合では観察されない、考慮された領域の現在の周期的変化[33]。 P の両方の分布 _s および P _v h に関して反対称です →− h 。フィールドの適切な調整により、完全なスピンと谷の分極を独立して達成することが可能です U および h 。たとえば、 h の場合 =6meVおよび U =42 meV、 P _s ≈1および P _v ≈1は、電流が主に K によって供給されることを意味します ↑ 電子。 h のとき =6meVおよび U =44 meV、 P _s ≈1および P _v P の間、≈-1 _s ≈-1および P _v h で≈-1 =6meVおよび U =46meV。結果は、スピンと谷の分極を効果的に切り替えることができることを示しています。

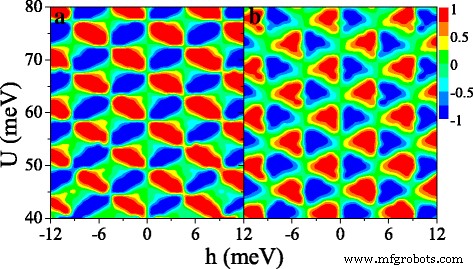
（ a の等高線図 ）スピン偏極 P _s （ U 、 h ）および（ b ）谷の分極 P _v （ U 、 h ）、Δで _z =10.0meV。他のパラメータの値は、図8の値と同じです

実験では、実験手法の限界により、モデルの構造的欠陥は避けられません。したがって、感染に対する障害の影響について議論する必要があります。電場または交換電場が無秩序を示す場合、コンダクタンス、スピン偏極、および谷分極を図1および2に示します。 10と11。Δの障害状況を設定します _z および h <Δで与えられる平均値を中心に変動します _z 〉 =Δ _{z 0} および〈 h 〉 = h ₀ 、 それぞれ。変動は

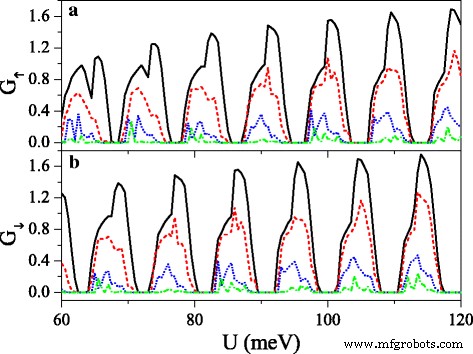
コンダクタンス（ a ） G _↑ および（ b ） G _↓ 対潜在的な U 、電界が無秩序を示す場合、 n =50およびΔ _{z 0} =20.0meV。実線、破線、点線、および一点鎖線の曲線は、無秩序の強さδに対応します。 =0.0、0.1、0.3、および0.6。他のパラメータの値は、図8の値と同じです

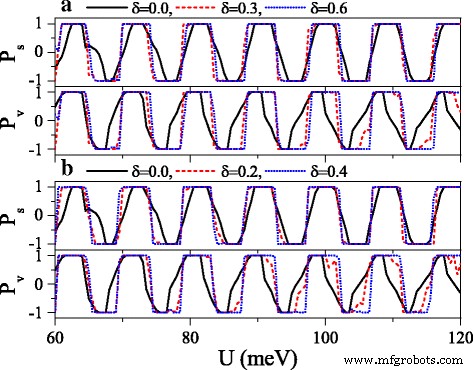
分極 P _s および P _v 対潜在的な U a の場合 電界または b 交換フィールドは無秩序を示します。 Δ _{z 0} =20.0meVおよび h =7.0 meV in（ a ）。 Δ _z =20.0meVおよび h ₀ =7.0 meV in（ b ）。他のパラメータの値は、図10の値と同じです

ここで、{ζ _i }は、無相関確率変数またはホワイトノイズのセットです。−1 <ζ _i <1、δ は無秩序の強さであり、 i サイトインデックスです。障害は x でのみ発生することに注意してください 方向、およびシステムは常に y で均一です 方向。したがって、 k _y まだ保全を続けています。図10は、コンダクタンスに対する電界の乱れの影響を示しています（a） G _↑ および（b） G _↓ 。障害の強さの存在と増加に伴いδ 、両方の G _↑ および G _↓ 徐々に抑制され、各共鳴ピークは多くの小さなピークに分割されます。コンダクタンスギャップ範囲が広がる一方で、コンダクタンス範囲が狭くなることがわかるかもしれません。したがって、 G の許容（または禁止）範囲 _↑ G の禁止（または許容）範囲に完全に該当します _↓ 、優れたスピン偏極を引き起こします（図11を参照）。さらに、コンダクタンスとコンダクタンスギャップの位置はδのようにほぼ不変です。 変化し、ミニバンドとバンドギャップが障害に鈍感であることを示唆しています。 G に対する電界の無秩序効果に注意してください。 _K および G _K ^' 図10で観察されたものと同様です。図11は、分極に対する（a）電界と（b）交換電界の無秩序な影響を示しています P _s および P _v 。明らかに、δの増加に伴い 、 P _s および P _v 大幅に増加し、偏光プラットフォームが広がります。したがって、完全なスピンと谷の分極が実現されます。図11aとbを比較すると、交換場の無秩序効果がより顕著であることがわかります。結果は、この無秩序が次数の場合と比較してスピンと谷の分極を強化する可能性があることを示しています。これは現実的なアプリケーションでの利点です。

結論

要約すると、周期的な場の下でのシリセンのバンド構造と輸送特性は、スピンと谷の自由度に強く依存することを詳細に示しました。数値結果は、スピンと谷が異なる電子は、ディラック点、バングギャップ、群速度にさまざまな特性を持っていることを示しています。特に、電場と交換場により、異方性速度が抑制され、特定のスピンと谷のコリメーション挙動を示します。したがって、透過率は、バンド構造と一致する、スピンと谷に依存する強い特徴を示し、スピンと谷の分極が大きくなります。さらに、この障害はスピンと谷の分極を大幅に強化する可能性があります。最後に、これらの結果がスピン指数と谷指数の潜在的な用途に役立つことを願っています。

略語

2D：

二次元

FM：

強磁性

SOI：

スピン軌道相互作用