GaAs / AlGaAs二次元電子ガスにおける外因性光誘起逆スピンホール効果の観測

背景

スピントロニクスは、情報技術への応用の可能性と、物性物理学における電子スピンの物理学に関する基本的な質問を明らかにすることで、大きな注目を集めています[1–4]。スピンホール効果（SHE）とそのオンセージャー相互作用である逆スピンホール効果（ISHE）は、スピン軌道相互作用を介して電荷電流をスピン電流に、またはその逆に変換する電気的方法を提供するため、スピントロニクスで重要な役割を果たします（ SOC）[2、5–8]。 SHEとISHEは、Pt、Ta、Py、IrMnなどの重元素を含む金属膜や、Bi ₂ などの新しいトポロジカル絶縁体で広く研究されています。 Se ₃ およびSnTe、SOCが強いため[9–14]。これらの2つの効果は、GaAs、ZnO、Si、Ge、GaN / AlGaN、GaAs / AlGaAs二次元電子ガスなどの半導体でも観察されます[15–20]。

半導体のスピンから電荷への電流変換は、スピントロニクスをエレクトロニクスと統合する道を開くため、重要な問題です[5]。光誘起ISHE（PISHE）は、半導体のISHEを調査するための効果的な実験ツールとして最近登場しています。これは、ガウス分布の円偏光を利用して半導体にスピン電流を導入し、ISHEを利用して電荷電流を生成します[ 2、19–22]。 PISHE電流は室温で観察でき、磁場や強磁性体を導入せずに半導体のISHEを調べるのに便利な方法です[20]。さらに、PISHEは新しい種類のスピンフォトニクスデバイスを設計する方法も提供します[22]。 PISHE電流は、GaN / AlGaN、GaAs / AlGaAs、およびMgZnO / ZnOヘテロ構造で観察されています[2、19、20]。ただし、PISHE電流の光パワーと光プロファイルへの依存性はまだ不明です。

ISHEには、内因性と外因性の2つのメカニズムがあります。内因性メカニズムは、ラシュバ[25–27]またはドレッセルハウスSOC [26]に由来する、完全に秩序化された材料[7、23、24]のバンド構造にのみ依存しますが、外因性メカニズムは、非対称のモットスキューまたは側面を指します。 -スピン軌道相互作用システムにおける不純物からのジャンプ散乱[16、24、28、29]。 ISHEの内因性または外因性のメカニズムを調査する研究はたくさんありますが、それらのほとんどは理論的研究であり、この問題に焦点を当てた経験的研究はほとんどありません[16、27、30–32]。実験的なメカニズム。

この論文では、GaAs / AlGaAs二次元電子ガス（2DEG）のPISHE電流を調べます。 PISHE電流は温度の上昇とともに増加することがわかり、PISHE電流は主に外因性メカニズムによって支配されていることを示しています。この推論は、サンプルの結晶方位に対するPISHE電流の弱い依存性によってさらに確認されます。さらに、PISHE電流の光パワーと光プロファイルへの依存性も調査します。これは理論モデルと非常によく一致しています。

メソッド

実験は、半絶縁性GaAs基板上に分子線エピタキシー（MBE）によって成長させた（001）配向の変調ドープGaAs / AlGaAs2DEGサンプルで実行されます。サンプルの電子密度とホール移動度は5.18×10 ¹¹ と測定されます。 cm ⁻² および3.97×10 ³ cm ² V ^-1 s ^-1 それぞれ室温で。 2DEGの移動度は、バックグラウンドドーピングのために少し低く、10 ¹⁵ のオーダーです。 または10 ¹⁶ cm ^-3 、サンプルの成長中に導入されたサンプル。サンプルは[110]および\（[1 \ bar {1} 0] \）方向に沿って10×10 mm ² の正方形に劈開されます。 。 [110]および[100]方向に沿ってそれぞれ8mmの距離にある2対のオーミック接触は、インジウム堆積によって作成され、窒素雰囲気中で約420°Cでアニールされます。

放射源として、波長1064nmのダイオード励起固体レーザーを使用します。レーザービームは、チョッパー、偏光子、および1/4波長板を通過し、最終的にサンプルを垂直に照射します。ここでは、偏光子と回転する1/4波長板を使用して、光のヘリシティを変更します P _c =sin2 φ 左利きから（σ ⁻ 、 P _c =− 1）から右利き（σ ⁺ 、 P _c =+ 1）継続的に、ここでφ は、入射光の偏光方向と1/4波長板の光軸との間の角度です。サンプルの光点はガウスプロファイルを持っています。電流は、プリアンプとチョッパーからの基準周波数229 Hzのロックインアンプによって、サンプルの[100]（または[110]）方向に沿って2つの接点間で収集されます。図1aは、PISHE電流の測定に使用されるセットアップを示しています。

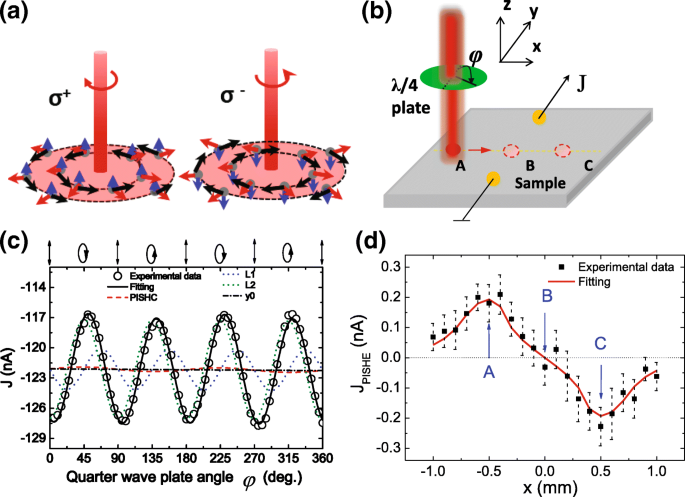
PISHE電流と300Kで測定されたPISHEを取得する方法。 a 左円偏光（σ）の通常の照明下でのスピン偏極電子の動きの図 ⁺ ）または右円偏波（σ ⁻ ） ライト。赤い矢印は電子の流れを示し、青い矢印は電子のスピン方向を示し、黒い矢印は電子に作用するスピン横力を示します。 b PISHE電流の測定に使用されるジオメトリ。 c 位相角φの関数として300Kで測定された光電流 点Aに光点が示されている場合の法線入射下。実線（黒）は、式（1）を使用したフィッティング曲線です。 （1）、破線（赤）はPISHE電流を表し、青と緑の点線は L を表します。 ₁ および L ₂ 成分。一点鎖線は、バックグラウンド電流 J を示します ₁ 。 d 300Kで測定された光スポット位置の関数としてのPISHE電流

パワー依存測定の場合、サンプルに照射される光のパワーは、減衰器を使用して250から40mWに変更されます。サンプル上の光点のプロファイルを変更するために、焦点距離の異なる光学レンズが採用されています。温度依存測定では、サンプルは光学クライオスタットに取り付けられ、77〜300Kの温度変化が可能になります。

ラシュバとドレッセルハウスSOCの相対比を取得するために、さまざまな結晶学的方向の円形光ガルバニック効果（CPGE）によって誘導される光電流を測定します。つまり、CPGE電流は、接点を介してそれぞれ[110]および[100]方向に沿って収集されます。 2つの接点の接続に垂直な光の入射面で。 CPGE測定では、[110]または[100]方向に沿った2つの接点の接続の中点、および入射角の範囲で光が斜めに照射されることを除いて、PISHE測定で使用されたものと同様の実験設定が採用されます。 −40から40°まで。特定の入射角でのCPGE電流は、光の偏光状態に依存する光電流 J をフィッティングすることによって抽出されます。 次の方程式[33]の2つの接点に沿って収集されます。 J = J _CPGE sin2 φ + L ₁₁ sin4 φ + L ₂₂ cos4 φ + J ₁₁ 。ここで、 J _CPGE はCPGE電流、 L ₁₁ および L ₂₂ は直線偏光によって誘発される光電流であり、 J ₁₁ は、光起電力効果またはデンバー効果から発生するバックグラウンド電流です[33]。

結果と考察

ガウスプロファイルの円偏光の照明下で、空間にガウス分布を持つスピン偏極キャリアが吸収不飽和領域で生成されます。その結果、半径方向に沿って流れる拡散スピン電流が現れます。次に、ISHE効果により、スピン偏極キャリアは接線方向に沿って「スピン横力」を経験し、軸方向に横方向の電荷電流、つまり渦電流（PISHE電流と呼ばれる）をもたらします[8、 20]、図1aに示すように。光の偏光状態が左側の円偏光（σ）から変化すると ⁺ ）右円偏光（σ ⁻ ）、電子のスピン偏極がスピンアップからスピンダウンに変化し、スピン横力とPISHE電流が逆転します。四分の一波長板が0から180°まで回転するとき、つまり角度φとして が0から180°に変更されると、光の偏光状態が垂直直線偏光（0°）から左側の円偏光（45°）、垂直直線偏光（90°）、右側に変更されます。図1cの上部に示すように、円偏光（135°）、および垂直直線偏光（180°）が続きます。したがって、角度としてφ が45°から135°に変更されると、PISHEが反転し、PISHEがsin2 φに比例することを示します。 。 φで注目に値する 角度が0、90、180°の場合、光は直線偏光になります。直線偏光は、 L と名付けられた光運動量整列効果[34]により光電流も誘導します。 ₁ 、または異方性光吸収[35、36]により、 L と名付けられました ₂ 。電流 L ₁ および L ₂ 直線偏光によって誘導される光は、sin4 φに比例します。 およびcos4 φ 、 それぞれ。その上、背景の光電流 J ₁ 光起電力効果またはデンバー効果に起因するものも存在しますが、これは光の偏光状態とは無関係です。したがって、角度φへの異なる依存性に応じて 、実験的に測定された光の偏光状態に依存する光電流 J をフィッティングすることにより、PISHE電流を抽出できます。 次の式に変換します[8、33]：

ここで J _PISHE は、左側の円偏光 L によって励起されたPISHE電流です。 ₁ および L ₂ は直線偏光によって誘発される光電流であり、 J ₁ バックグラウンド電流です[19]。 L に注意する必要があります ₂ 項はフィッティング方程式に含まれています。 （1）、サンプルに存在する大きな光学異方性のため。光学異方性は、異方性界面構造[37]、原子の分離[38]、または残留応力[39]によって引き起こされる可能性があります。

PISHEの空間分布を取得するために、垂直二等分線に沿って2つの接点の左側から右側にレーザースポットを掃引します[図1aを参照]。各スポット位置で、1/4波長板を0から360°まで回転させ、式（1）をフィッティングすることによってPISHE電流を取得します。 （1）実験的に測定された光の偏光状態に依存する光電流 J 。図1bは、位相角φの関数として測定された光電流の典型的な結果を示しています。 、レーザースポットが x に固定されている場合 =− 0.5 mm、つまりポイントAで[図1aを参照]。光電流は300Kで測定され、[110]方向に沿って2つの接点に沿って収集されます。サンプル上のレーザースポットの直径は約1.4mmで、ガウスプロファイルと出力は250mWです。図1bの円は実験データであり、実線は式（1）によるフィッティング結果です。 （1）。実験的に測定された光電流は、1/4波長板を回転させると周期的に変動することがわかります。これは、光電流がPISHE電流、直線偏光によって誘導される光電流、およびバックグラウンド電流の合計であり、角度φに対して異なる依存性を示すためです。 。一点鎖線はPISHE電流を示し、一点鎖線はバックグラウンド電流を示します。青と緑の点線は L を表します ₁ および L ₂ それぞれ直線偏光によって誘発される成分。 PISHE電流は、直線偏光によって誘導される光電流よりもはるかに小さいことがわかります。

得られたスポットの関数としてのPISHE電流を図1cに示します。レーザースポットが2つの接点の左側から右側に移動すると、PISHE電流の方向が逆になることがわかります。レーザースポットが2つの接点の中点に焦点を合わせると、PISHE電流はほぼゼロになります。この現象は、光誘起逆スピンホール効果によって誘発される渦電流モデルによって定量的に説明することができます[20]。具体的には、ガウスプロファイル G のレーザーの放射下で （ r ）=\（\ frac {1} {\ sqrt {2 \ pi} \ sigma} \ exp \ left（-\ frac {r ^ {2}} {2 \ sigma ^ {2}} \ right）\）、半径方向に沿って流れるスピン電流が誘導されます。これは j として表すことができます。 _r =τ _s D ∇ _r G （ r ）。ここで、 D はスピン拡散係数τです。 _s はスピン緩和時間、 r は半径方向を示し、σ 光強度の半値全幅（FWHM）に関連する分布分散を示します。 ISHE効果により、スピン偏極キャリアはスピン横力\（f（r）\ p​​ropto j_ {r} \ times \ hat {z} \）[20、40]を経験します。これは、\（ f（r）=-f_ {0} r / \ sigma ^ {3} \ exp \ left（-\ frac {r ^ {2}} {2 \ sigma ^ {2}} \ right）\）。ここで、 f ₀ は、材料系のSOCに関連するスピン横力定数です。渦電場\（\ vec {E} \）は、円起電力（EMF）によって決定できます。これは、\（\ varepsilon（r_ {0}）=\ frac {2 \ pi} {q } \ int _ {0} ^ {r_ {0}} f（r）rdr \）、〜\（\ oint \ vec {E}（r_ {0}）\ cdot d \ vec {l} =\ varepsilon（ r_ {0}）\）。ここで、 r ₀ は光点の半径であり、積分ループは光点の周囲に沿っています。したがって、

式のわずかな違いは注目に値します。 （2）と[20]で報告されているのは、この論文では正規化されたガウス関数が採用されているのに対し、[20]では正規化されていないガウス関数が使用されているためです。 f ₀ このペーパーでは、 f と同等です。 ₀ / σ [20]で報告されています。 2つの接点間の電流（ a という名前） および b 、それぞれ）は

ここで、 V _ab （ R _ab ）は、接点間の電圧（抵抗）です a および b 、 o は光点の原点であり、 S abo の三角形の領域を示します 。サンプルによって吸収される光強度が一定であり、サンプルの最大吸収に達する吸収飽和領域は、式（1）の積分から差し引かれるべきであることに注意する必要があります。 （3）。これは、その領域で光生成キャリアの勾配がゼロであり、その結果、その領域でスピン電流とPISHE電流がすべてゼロになるためです。

注目に値するのは、式（3）連絡先が a の場合にのみ成立します および b ライトスポットの外側にあるため、ライトスポットで覆われています。 （2）は無効になりました。したがって、外部の電流（ J _f ）および内部（ J _e ）スポット、つまり J _f =\（J_ {e} \ exp \ left（-\ frac {l} {A \ cdot L_ {s}} \ right）\）[41]、式を表すことができます。 （3）as：

ここで、 l は、光スポットのエッジと2つの接点の接続 L の間の距離です。 _s は電子の拡散長であり、 A 定数です。式を使用します。 （2）と（4）実験的に測定されたPISHE電流に合わせるために、スピン横力 f を得ることができます。 ₀ 拡散長 A ・ L _s 。フィッティング結果は図1cに実線で示されています。実験データがモデルによく適合していることがわかります。フィッティングでは、実験的に測定された次のパラメータσが採用されています。 =0.2 mm、 L =4 mm、 r ₀ =0.7 mm、および R _ab =15.5 k Ω 。スピン横力 f ₀ / q 電子の数は6.8×10 ^-6 に適合します N・m / C、300 K、 A ・ L _s 2.8×10 ^-4 になるように取り付けられています mであり、吸収飽和領域の半径は0.34 mmに適合しています。これは、光の吸収飽和強度が I であることを示しています。 _c 最大強度の約5分の1に相当します I _m 、つまり I _c =1/5 I _m 。

PISHE電流の光パワーおよび光プロファイルへの依存性を調査するために、さまざまな光パワーおよびさまざまな光プロファイルの下でPISHE測定を実行します。図2a、bは、光スポット半径が r のさまざまな光パワーの下での光スポット位置の関数としてのPISHE電流を示しています。 ₀ =1.5mmおよびσ =0.5mmおよび r ₀ =1mmおよびσ =それぞれ0.3mm。記号は実験データであり、実線は式（1）による理論計算です。 （2）と（4）。計算では、図1cで採用されているライトスポットパラメータを除いて、同じパラメータ、つまり f が使用されます。 ₀ / q =6.8×10 ⁻⁶ N・m / C、 A ・ L _s =2.8×10 ⁻⁴ m、 R _ab =15.5 k Ω 、および I _c =1/5 I _m 。ここで、私 _m は、電力が250mWのときの光の最大光強度です。 PISHE電流の強度は、光のパワーとともに増加し、250 mWのパワーの下では、FWHMが大きい（つまり、σが大きい）光スポットであることがわかります。 ）より大きなPISHE電流につながります。また、FWHMが大きい光スポットの場合、PISHE曲線のピークが x の大きい値で現れることもわかります。 。ここで、 x は、光点の中心と2つの接点の接続の中点との間の距離です。これは、スピン電流とその結果生じるPISHE電流が光プロファイルの勾配に比例するためです。さまざまな光スポットプロファイルによって誘導されるPISHE電流をより適切に比較するために、図2cの図2a、bの結果を要約します。つまり、さまざまな場合の励起電力に対するPISHE電流のピーク値の依存性を要約します。図2cの光点プロファイル。記号は実験データを示し、実線は理論計算結果です。実験結果が理論シミュレーションと非常によく一致していることがわかります。これにより、モデルが確認されます。

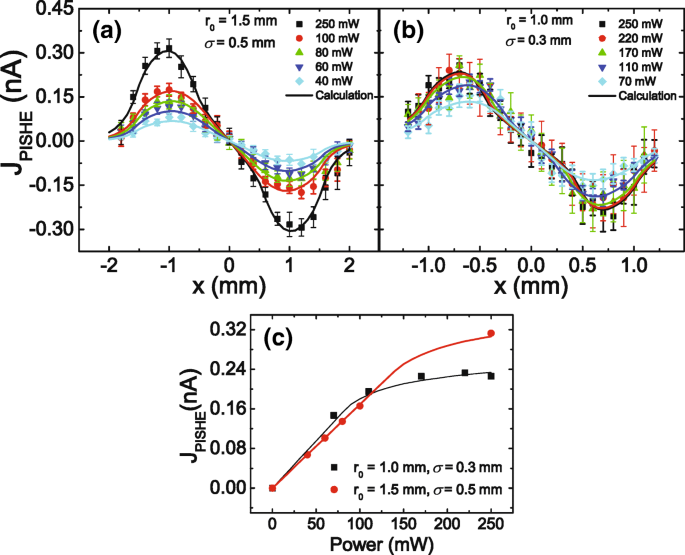
異なる光パワー下での光スポット位置の関数としてのPISHE電流。 a 、 b r のガウスプロファイル光スポットによって励起されたPISHE電流 ₀ =1.5mmおよびσ =0.5mmおよび r ₀ =1mmおよびσ =それぞれ0.3mm。 c 記号と実線がそれぞれ実験データと理論計算結果である、励起パワーによるPISHE電流のピーク値の変化

図2cは、電力が増加すると、PISHE電流が最初に単調に増加し、次に徐々に飽和することを示しています。光パワーによるPISHE電流の飽和の出現は、高パワーでの吸収飽和の存在によるものです。最大光強度が吸収飽和強度よりも小さい場合、PISHE電流は光パワーに比例して増加します。最大光強度が吸収飽和強度よりも大きい場合、PISHE電流は光パワーの増加とともに飽和する傾向があります。光スポットサイズとＦＷＨＭは光パワーによって相互に相関しているので、光スポットサイズがＰＩＳＨＥ電流に及ぼす影響は、光スポットのＦＷＨＭがＰＩＳＨＥ電流に及ぼす影響の観点から理解することができる。具体的には、特定の光パワーの場合、光スポットのサイズが大きいほど、FWHMの値が大きくなります。特定の光パワーで、最大光強度が吸収飽和強度よりも小さい場合、FWHMが小さい（つまり、光スポットのサイズが小さい）光プロファイルは、より大きなPISHE電流を生成できます。これは、FWHMが小さいほど大きくなるためです。スピン電流;一方、最大光強度が吸収飽和強度よりも大きい場合、FWHMの値が小さい光プロファイルでは、PISHE電流が小さくなります。これは、さまざまな光プロファイルの下での光スポット位置の関数としてのPISHE電流をまとめた図3でもはっきりと見ることができます。光のパワーは250mWです。 σの値として、 0.2mmから0.5mmに増加すると、PISHE電流のピーク値は単調に減少します。これは、吸収飽和領域ではスピン電流が発生せず、その結果、PISHE電流が発生しないためです。したがって、吸収飽和領域内の光はPISHE電流に寄与しません。図3の挿入図は、さまざまなガウス光プロファイルの光強度の分布を示しています。破線はサンプルの吸収飽和強度を表しています。破線と光強度曲線の交点は、吸収飽和領域の半径を示し、 r で表されます。 _s 。半径 r の円形領域内の光 _s 、 r のときに影の領域で示されます ₀ =1.5およびσ =0.5 mm、PISHE電流には寄与しません。 250 mWの光パワーの場合、FWHMが小さい光プロファイルでは、吸収不飽和領域でのスピン電流が大きくなりますが、この効果は、吸収飽和領域で浪費されるエネルギーが増えることで圧倒されることがわかります。その結果、σの値が小さいライトプロファイル （つまり、σ =0.2 mm）は、σが大きい場合よりも小さい値のPISHEを生成します。 （つまり、σ =0.3または0.5mm）。

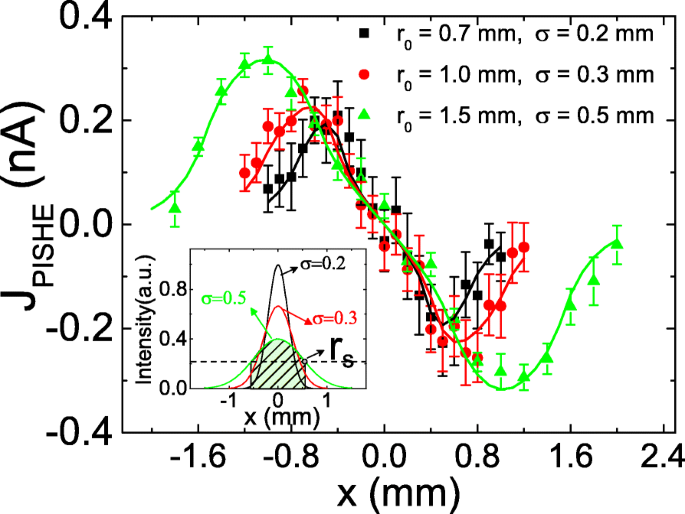
光出力が250mWの場合の、さまざまなガウス光プロファイルの下での光スポット位置の関数としてのPISHE電流。挿入図は、さまざまなガウス光プロファイルの光強度の分布を示しています。破線はサンプルの吸収飽和強度を示します

PISHEの主要なメカニズムを調査するために、さまざまな温度でPISHE測定を実行します。図4aは、77、130、180、および230 Kで測定された光スポット位置の関数としてのPISHE電流を示しています。レーザースポットは、 r のガウスプロファイルを持っています。 ₀ =0.7mmおよびσ =0.2 mm、電力は250mWです。四角は実験データを示し、実線は式を使用したフィッティング結果です。 （2）と（4）。実験データはすべて、すべての温度でモデルによく適合していることがわかります。フィッティングにより、スピン横力 f を得ることができます。 ₀ / q 、図4bに示されている、および電子の拡散長 A ・ L _s さまざまな温度で。図4bの破線は目のガイドです。パラメータ A の値を決定するには 、 A の温度依存性を比較する必要があります ・ L _s 電子拡散長 L の温度依存性の以前の結果に _s 。 A の値をフィッティングすることによって ・ L _s L の値に _s [42]で得られた、定数 A を決定できます 1.65×10 ² になります 。図4cに示した以前の結果との結果の非常に良い一致は、私たちの方法を検証します。電子拡散長は温度の上昇とともに減少することがわかります。これは主にフォノンによるキャリア散乱の増強に起因する可能性があります[43]。

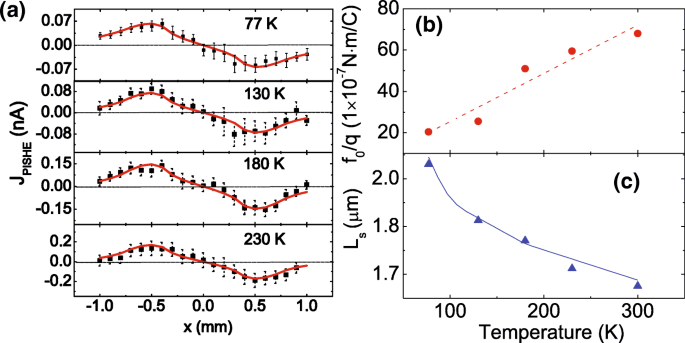
GaAs / AlGaAs 2DEGのPISHE電流、スピン横力、および電子拡散長の温度依存性。 a さまざまな温度で測定された光スポット位置の関数としてのPISHE電流の実験およびモデリング結果。実線の四角は実験データであり、実線はフィッティング結果です。 b 、 c それぞれ温度の関数としてのスピン横力と電子拡散長。 b の破線 は目のガイドであり、 c の実線です。 [42]

から取得されます

驚いたことに、スピン横力 f ₀ / q 2DEGの温度は温度の上昇とともに単調に増加します。これは、Au / InPハイブリッド構造で観察されたPISHEの温度で逆の変動傾向を示しています[44]。この予期せぬ現象は、PISHEのメカニズムに関係している可能性があります。半導体2DEGのPISHEには、内因性メカニズムと外因性メカニズムの2つのメカニズムがあります。前者は主にバンド構造に起因し、後者は不純物のSOC効果による上下スピンの散乱の非対称性に起因します[7、16]。 C の半導体2DEGの場合 _{2 v} 点群対称性、固有のメカニズムによって誘発されるスピン横力は、\（f_ {0} =\ frac {4m ^ {* 2} \ tau _ {s} D} {\ hbar ^ {2}} \ left （\ alpha ^ {2} + \ beta ^ {2} \ right）\）[20、40]、ここで\（\ hbar \）は縮小プランク定数τ _s はスピン緩和時間、 D はスピン拡散係数であり、α （またはβ ）は、ラシュバ（またはドレッセルハウス）SOCの強度に比例するラシュバ（またはドレッセルハウス）定数です。 GaAs / AlGaAs 2DEGの場合、スピン緩和時間τ _s T に比例します ^-1 [45]。ここで、 T 温度を表します。変調ドープ2DEGの場合、ラシュバSOCの強度はドレッセルハウスの強度よりもはるかに大きくなります（次の説明を参照）。その結果、ラシュバ定数α ドレッセルハウス定数βよりもはるかに大きい 。スピン拡散係数 D T に比例します ⁻² [46、47]。 αの温度依存性 a として表すことができます + b T 、ここで a および b は定数であり、 a b より約2桁大きい [48]。したがって、τの温度依存性を考慮に入れる _s 、 D 、およびα 、 f があります ₀ ∝ T ^-3 、これは、固有のメカニズムによって誘発されるスピン横力が温度の上昇とともに減少するはずであることを示唆しています。外因性メカニズムの場合、特に外因性サイドジャンプ散乱の場合、スピン横力はイオン化不純物の濃度に依存します[49、50]。サンプルにはバックグラウンドドーピングがあり、温度の上昇とともに不純物のイオン化が増加するため、温度の上昇とともにスピンアップおよびスピンダウン電子の非対称散乱が強くなり、温度の上昇とともにスピン横力が大きくなります。スピン横力 f ₀ 私たちの実験で観察されたように、温度の上昇とともに増加しますが、PISHEは外因性メカニズムによって支配されていると推測できます。このメカニズムでは、不純物は主に成長プロセス中のバックグラウンドドーピングによって導入されます。

PISHEが実際に外因性メカニズムによって支配されていることをさらに確認するために、さまざまな結晶方向に沿って収集されたPISHE電流の空間分布を測定します。図5a、bは、それぞれ[110]および[100]結晶方向に沿って収集されたPISHE電流の空間分布を示しています。異なる結晶方向のキャリア移動度とキャリア密度の影響を排除するために、対応する光電流 J によってPISHE電流を正規化します。 ₀ 接点がそれぞれ[110]および[100]方向に沿っている場合、0.3Vのバイアス下で。測定は、60mWの電力の放射の下で室温で実行されます。光点半径 r ₀ は1.0mmで、σ 0.3mmです。記号は実験データを示し、実線は式（1）によるフィッティング結果です。 （2）と（4）。 [110]と[100]の結晶方向に沿って収集された正規化されたPISHE電流の間に顕著な違いがないことがわかります。

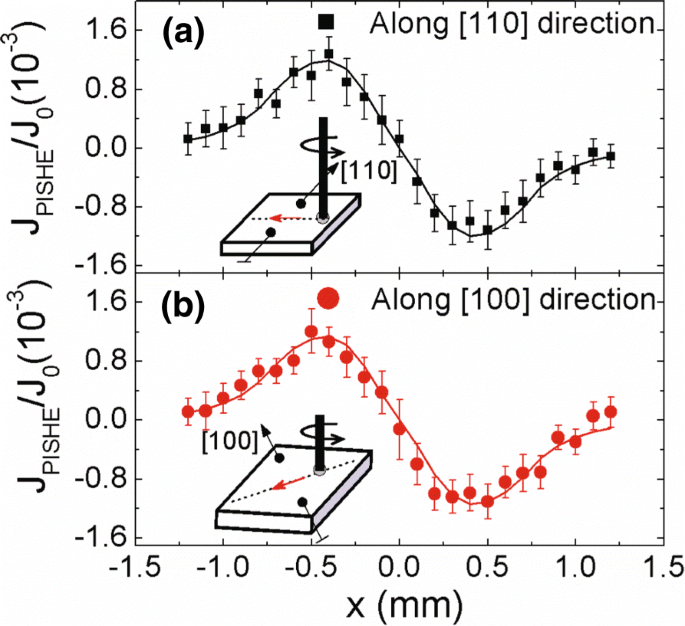
さまざまな結晶方位に沿って収集された正規化されたPISHE電流。 PISHE電流は、0.3 Vのバイアス下での光電流によって正規化されます。実線の記号は実験データであり、実線は理論上のフィッティング結果です。挿入図は、対応する測定形状の概略図を示しています

固有のメカニズムの場合、特定の結晶方向に沿ったPISHE電流は、その方向でのスピン分裂に関連しています。 GaAs / AlGaAs 2DEGの異方性スピン分裂の知識を得るために、室温でのCPGE電流の結晶方位依存性を測定します。つまり、2つの接点が[110]（または[100]に沿っている場合のCPGE電流を測定しました。 ]）方向と光の入射面は[1 \（\ bar {1} \）0]（または[010]）方向にあり、その測定結果は図6に四角（または丸）で示されています。 。CPGE電流を測定する場合、光点は2つの接点の接続の中間点にあり、[20]によるとPISHEはゼロです。 CPGE電流は、0.3 Vのバイアス下で対応する光電流によっても正規化され、さまざまな結晶方向のキャリア移動度とキャリア密度の影響を排除します[51]。次に、次の式を使用して、正規化された角度依存のCPGE電流を適合させ、さまざまな結晶方向に沿った相対的なSOC強度を取得します[21、27]。

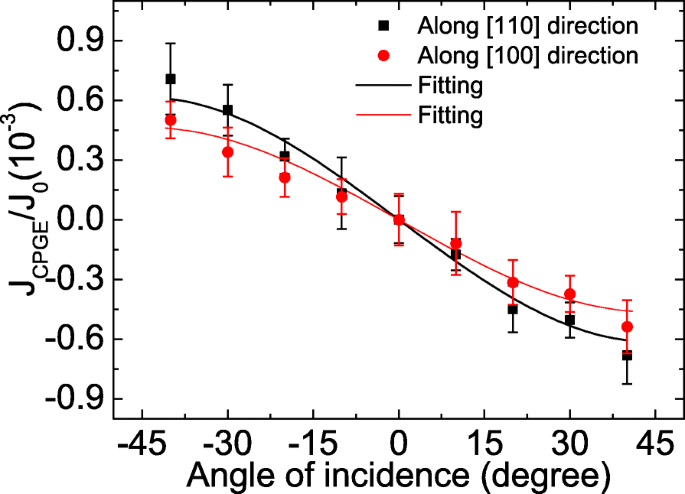
異なる結晶方位に沿って収集された正規化されたCPGE電流の入射角依存性。 CPGE電流は、0.3 Vのバイアス下での光電流によって正規化されます。実線の記号は実験データであり、線は式（1）によるフィッティング結果です。 （5）

ここで、θ は入射角、 n はGaAsの屈折率であり、 A _λ はSOC定数に比例する定数です。フィッティングの結果を図6の実線で示します。光の入射面が[1 \（\ bar {1} \）0]方向にあり、CPGE電流が[110]方向に沿って収集される場合、対応する A A として示されるパラメータ _[110] は、ラシュバとドレッセルハウスのSOCの合計に比例します。つまり、 A _[110] ∝ α + β [51–53]。光の入射面が[010]方向にあり、CPGE電流が[100]方向に沿って収集される場合、対応する A A として示されるパラメータ _[100] 、はラシュバSOCに比例します。つまり、 A _[100] ∝ α [51–53]。したがって、 A の比率によって _[110] / A _[100] 、ラシュバとドレッセルハウスSOCの相対比、つまり\（\ beta / \ alpha =\ frac {A _ {[110]}} {A _ {[100]}}-1 \）=0.32を取得できます。これは、 GaAs / AlGaAs2DEGのスピン分裂には結晶異方性があること[21]。したがって、PISHEへの本質的な寄与は、結晶軸に敏感である必要があります[16]。具体的には、式によると。 （2）および（4）、接点が[110]（または[100]）方向に沿っている場合、測定されたPISHE電流は、[110]（または[100]）方向にほぼ平行に流れる逆スピンホール電流によって支配されます。 PISHE電流は渦電流であるため。固有のメカニズムが2DEGで支配的な役割を果たす場合、これら2つの方向に沿って収集されるPISHE電流は異なるはずです。ただし、顕著な違いは見られず、これは、GaAs / AlGaAs2DEGでは外因性メカニズムが支配的であることを示唆しています。

結論

結論として、GaAs / AlGaAs 2DEGのPISHE電流は、77〜300 Kの温度範囲で調査されました。スピン横力は、PISHE電流を理論モデルに適合させることによって決定されました。 PISHEの光パワーおよび光スポットプロファイルへの依存性が調査されており、理論モデルとの良好な一致を示しています。温度によるPISHE電流の変化は、PISHEが外因性メカニズムによって支配されていることを示唆しています。これは、サンプルの結晶配向に対するPISHE電流の弱い依存性によってさらに確認されます。

略語

2DEG：

二次元電子ガス

CPGE：

円形の光ガルバニック効果

EMF：

円形起電力

FWHM：

半値全幅

ISHE：

逆スピンホール効果

MBE：

分子線エピタキシー

PISHE：

光誘起逆スピンホール効果

SHE：

スピンホール効果

SOC：

スピン軌道相互作用