バルクディラック半金属-絶縁体-金属導波路におけるテラヘルツ表面プラズモンポラリトンの閉じ込めの強化
要約
バルクディラック半金属(BDS)-絶縁体-金属(BIM)構造に基づくサブ波長テラヘルツプラズモン導波路が調査されます。これは、より良い閉じ込めとより低い損失を備えた最適化された周波数範囲があることを示しています。 λまでのブロードバンドモードの制限 0 / 15、1.0 dB / λの比較的低い損失 0 達成することができます。また、BIM導波路に導入された2つのシリコンリボンが、動的に調整可能なフィルターを形成し、テラヘルツ表面プラズモンポラリトンを深サブ波長スケールで調整できることを示します。これは、動的に調整可能な超小型THzプラズモンデバイスの設計にさらに活用できます。私たちの結果は、光学フィルタリングの潜在的なアプリケーションも提供する可能性があります。
背景
テラヘルツ(THz)波は、THzイメージング、生化学的センシング、通信などの革新的なアプリケーションで、過去数十年で非常に目撃されてきました[1,2,3]。テラヘルツデバイスのセンシング感度、イメージング解像度、統合レベルを向上させるために、テラヘルツ波を深いサブ波長スケールに閉じ込めることが緊急に望まれています[4,5,6]。表面プラズモンポラリトン(SPP)は、貴金属の伝導帯の電子と可視波長の光子との相互作用によって刺激され、金属と絶縁体の界面に沿って伝播し、古典的な回折限界を超える光の操作を可能にします[7]。可視帯域のSPPのアナログであるSommerfeld-Zenneckモードは、THz領域の金属でサポートできます。メタマテリアルや、周期的なパッチ、穴あきプレート、真ちゅう製のチューブなどの他の人工構造物が、この緩く結合した表面波を調整するために提案されています[8、9、10]。残念ながら、このモードの不十分な閉じ込め、高い固有損失、および受動的な調整可能性は、その実際のアプリケーションを大幅に妨げています。
グラフェンプラズモンは、損失が比較的少なく、動的に調整可能で、THz波に極端に閉じ込められているため、高解像度、超小型、動的に調整可能なデバイスで有望なアプリケーションを保持します。 Duan etal。動的な調整可能性とより高い効率でテラヘルツプラズモンをコヒーレントに生成および制御するための広帯域ゲート調整可能なグラフェンヘテロ構造を提案します。グラフェンプラズモン場の緊密な閉じ込めにより、ロバストな差周波数信号を生成できます[11]。 Duan etal。最初に、THz波長での誘電体グラフェンプラズモニック導波路アレイにおける離散タルボット効果を調査します。これは、ナノスケールでのTHz波の高解像度自己像化のための新しいプラットフォームを提供します[12]。リンら。超小型プラズモン誘起透明導波路を提案します。これは、THz波の低速光での潜在的なアプリケーションを約束します[13、14]。 Li etal。高積分[15]、低損失、動的調整可能性[16,17,18]を示す、2D材料プラズモンに基づく一連の機能的な光学フィルターと吸収体を提案します。これらの研究から、テラヘルツ波を深いサブ波長スケールで操作することを可能にするのは、表面プラズモンの極端な閉じ込めであると確信することができます。
最近、バルクディラック半金属(BDS)である「3Dグラフェン」が、最大9×10 6 の超高速キャリア移動度により注目を集めています。 cm 2 V -1 s -1 、これは2×10 5 の最高のグラフェンよりもはるかに高いです cm 2 V -1 s -1 [19]。一般に、キャリア移動度が高いほど、プラズモンの固有損失は低くなります。さらに、BDSの誘電関数は、フェルミエネルギーを変更することでアクティブに調整できます。良いニュースは、Na 3 などのBDSです。 Bi [19]、Cd 3 As 2 [20]およびAlCuFe準結晶[21]は、グラフェンに続く新世代のプラズモン材料であると期待されるグラフェンと比較して、処理が容易で安定しています。ただし、BDS-insulatorインターフェイスでのSPPのモード制限は楽観的ではありません。私たちの最近の研究は、2層BDSシート導波路でのTHz SPPの操作を調査しました。これは、対称結合モードが単層BDSフィルムのプラズモン導波路モードよりも優れた閉じ込めを持っていることを示しています[22]。対称モードのモードインデックスは、BDS E のフェルミエネルギーで1.0THzで1.21です。 F =70 meV。これは、深部サブ波長スケールでTHz波を操作するという要求を満たすにはまだ不十分です。
この論文では、閉じ込めが強化され、損失が比較的低く、調整可能性が望ましい、深サブ波長のBDS絶縁体金属(BIM)導波路を提案します。この高度に制限されたモードの分散関係、伝搬損失、およびフィルタリングアプリケーションが調査されます。興味深いことに、金属構造の従来のSPPモードではめったに報告されていない、閉じ込めが強化され、損失が低減された最適化された周波数範囲があります。 λまでのブロードバンドモードの制限 0 / 15、1.0 dB / λの比較的低い損失 0 達成することができます。以前に研究されたBDSベースの構造とは異なり、このBIM導波路のモードは、λよりも小さい幅の超狭スリットを効率的に伝送できます。 0 / 2000。 2本のシリコンリボンを反射鏡として採用することで、動的に調整可能な光共振器を実現しました。共振器の共振周波数は、BDSのフェルミエネルギーを変化させることで動的に調整できます。これにより、THzスイッチングとフィルタリングに応用できる可能性があります。
理論とシミュレーション
提案されたBIMプラズモン導波路を図1(a)に模式的に示します。ここでは、厚さ0.2μmの単層BDSフィルムがギャップ幅 g に配置されています。 誘電率εで誘電体スペーサーによって分離された銀基板から離れる r 。 THz領域の銀基板は、完全電気導体(PEC)境界として扱うことができます。 TM偏光の入射光の場合、金属-絶縁体界面に閉じ込められたプラズモン導波路モードは、 x に沿って伝播する可能性があります。 波数ベクトル k による方向 SPP y に沿って指数関数的に減衰します 自由空間への方向。適切な境界条件を組み合わせることにより、波数ベクトル k SPP BIM導波路の振幅は、次の分散関係から取得できます。[23]。
$$-\ frac {\ varepsilon_r \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} {\ varepsilon_0 \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac { \ varepsilon_r {k} _0 ^ 2} {\ varepsilon_0}}} =\ left(1+ \ frac {i \ sigma \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} { {\ omega \ varepsilon} _0} \ right)\ tanh \ left(g \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac {\ varepsilon_r {k} _0 ^ 2} {\ varepsilon_0}} \ right )、$$(1)ここで k 0 は入射光の波数ベクトルです。式を解くことによって。 (1)、実効屈折率 n を得ることができます。 eff = k SPP / k 0 =Re( n eff )+ i Im( n eff )提案されたプラズモン導波路の。高度に閉じ込められたプラズモン導波路モードの場合、実効屈折率Re( n の実数部 eff )虚数部Im( n eff )はモード伝搬損失に正比例します。Re( n が大きいほど eff )は、閉じ込めが高くなります。 g の場合 tanh [ g ( k SPP 2 − ε r k 0 2 / ε 0 )] 〜1、式(1)分散関係に還元されます
$$-\ frac {\ varepsilon_r \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} {\ varepsilon_0 \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac { \ varepsilon_r {k} _0 ^ 2} {\ varepsilon_0}}} =\ left(1+ \ frac {i \ sigma \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} { {\ omega \ varepsilon} _0} \ right)、$$(2)これは、BDSの単層のみでサポートされるプラズモン導波路モードを示しています。 BDSの複素伝導率は、式(3)〜(4)の方法で表されます。
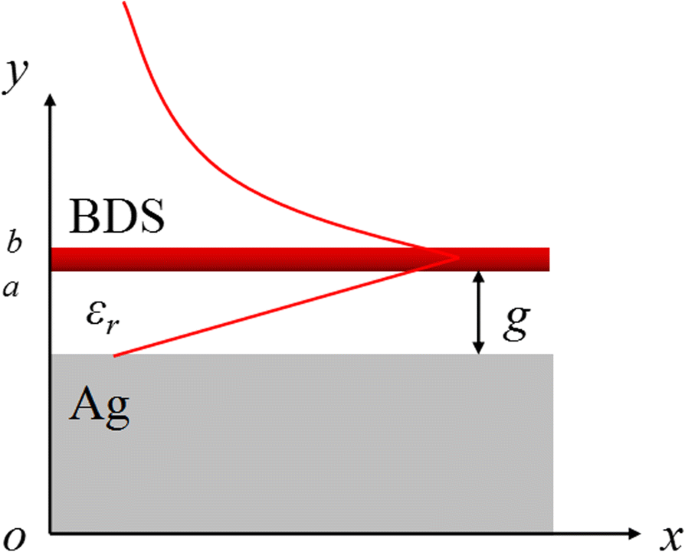
BIMプラズモン導波路の概略図:単層BDSフィルムがギャップ幅 g に配置されています 誘電率εの誘電体スペーサーで分離された銀基板から離れる r 。 TM偏光プラズモン導波路モードは x に沿って伝播します 方向と y に沿った減衰 方向。 E の概略図 x 分布は赤い線で示されています
結果と考察
まず、BIM導波路のモード閉じ込めと伝搬損失のBDS-金属ギャップ幅 g への依存性を示します。 とフェルミエネルギー E F 。 E を取ることによって F =70 meV、SPP導波モードの実効屈折率を計算します n eff g のさまざまな値の場合 、実数部と虚数部、Re( n eff )およびIm( n eff )は、それぞれ図2a、bにプロットされています。図2aに示すように、 g の曲線 =10と100μmは0.05THzより高い周波数で融合します。これは、プラズモニック導波路モードがBDS-絶縁体インターフェースに非常に緊密に閉じ込められているため、ほとんどのSPPフィールドが10μmのスケール内に分散され、銀が機能しないことを示しています。そのような大きなギャップ幅で。ギャップ幅 g の後、モードの制限が劇的に強化されます。 g が小さい1μmから徐々に減少します 研究し、より強い閉じ込めを得ることができます。同様の傾向は、伝搬損失のギャップ幅 g への依存性にも見られます。 、図2bに示すように。一方、1μm未満の固定ギャップ幅の場合、Re( n eff )それぞれが最初に最小値への顕著な減少を示し、その後徐々に増加する動作を示しますが、Im( n eff )周波数が高くなると、それぞれが単調に減少します。したがって、伝搬損失が徐々に減少する一方で、モード閉じ込めが強力に強化される最適化された周波数領域があります。この特性は、金属-絶縁体界面の従来のプラズモン導波路モードではめったに観察されていません。図2c、dは、モード閉じ込めと伝搬損失のフェルミエネルギー E への依存性を示しています。 F ギャップ幅 g であるBDSフィルムの =1μm。単層および二重層導波路の場合と同様に、モード閉じ込めと伝搬損失はフェルミエネルギーの増加とともに連続的に減少します。これは、BDSの金属量の向上とキャリア緩和時間の延長に起因する可能性があります。たとえば、2.5THzでのプラズモン導波路モードの閉じ込め係数は最大λになります。 0 / 15、ここでλ 0 入射波長、1.0 dB / λの比較的低い損失 0 BDS-金属ギャップ幅が10nmで、フェルミエネルギーが70meVの場合。したがって、すでに上で説明したフレームワークに依存すると、比較的低損失でモード制限が増加し、統合された光学フィルター、バッファー、およびマッハツェンダー干渉計の設計に利用できます。
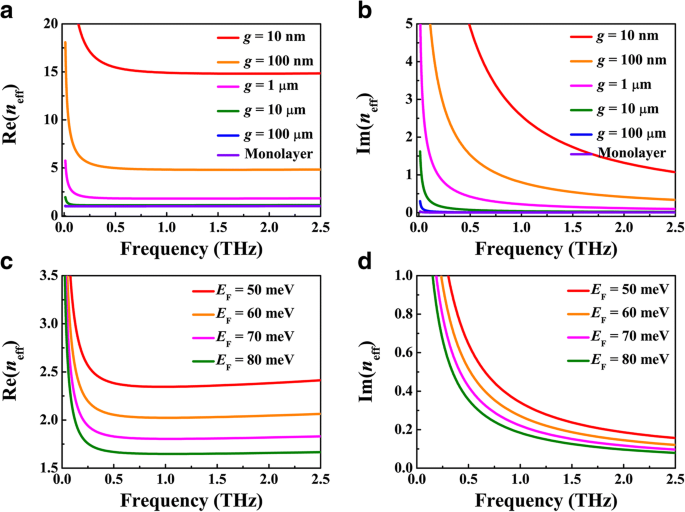
実効屈折率の実数部と虚数部 n eff a の場合 、 b 異なるギャップ幅 g 、BDSのフェルミエネルギーが E に固定されている場合 F =70 meV、および c 、 d フェルミエネルギーのさまざまな値 E F 、ギャップ幅は g =に固定されています 1μm
前述の分析を検討するために、提案された導波路構造の透過強度と電界分布について数値計算を実行します。シミュレーション設定はメソッドで説明されています。同じフェルミエネルギーの単層BDS導波路との比較 E F =70 meV、1.56 THzの周波数でのBIM導波路の透過強度は0.97であり、図3aに示すように、前者の透過強度よりも高くなっています。これは、BIM構造のプラズモン導波路モードの伝搬損失が低いことを示しています。一方、図2aに示すように、1.56 THz Re( n でのBIMの実効屈折率の実数部 eff )=2.45、これは単層の場合の1.002よりもはるかに高いです。このステートメントを視覚化するために、磁場 Hz これらのモードの分布を図3b、cに示します。 BIM導波路の高度に閉じ込められたプラズモンモードは、単層BDSの場合よりも短い発振周期を示すことがはっきりとわかります。さらに、プラズモン場のほとんどはそのような狭いスリットに局在しています〜λ 0 / 2000、非線形物理学の近接場増強における有望なアプリケーションを保持します。
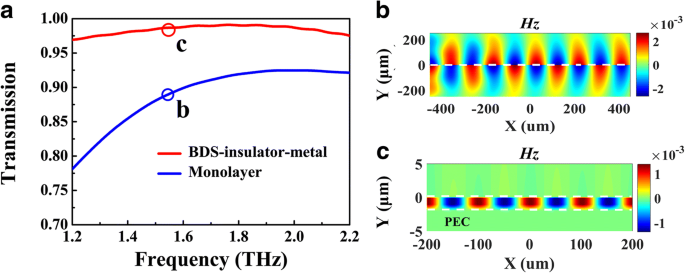
透過スペクトルの数値計算( a )および磁場( H z )分布( b 、 c )BIM(赤い曲線)と単層(青い曲線)の導波路。ここで、 E F =70 meV、 g =50 μ m、および1.56THzの入射頻度
上記のすべてのアプリケーションの中で、光共振器は、THzプラズモン導波路モードを調整するための重要な要素です。図4aに示すように、2つのシリコン( n Si =3.4)[24]リボンは誘電体スペーサーに埋め込まれて反射ミラーを形成します。ここで、伝播するプラズモニック波はシリコンと空気の界面で前後に反射し、2つのシリコンリボン間のBIM領域に局所的な定在波共鳴を形成します。 。入射周波数のみが定在波の共振条件を満たすため、プラズモニック波は設計された光共振器との結合を介して導波路の出力に送信できます。図4aは、2つのシリコンリボンを備えたBIM導波路の透過スペクトルを示しています。ここで、FWHM(半値全幅)の値が0.12および0.09 THzの2つの透過ピークが、1.56および2.22THzの周波数で明らかに見られます。テラヘルツ領域でのバンドパスフィルタリング効果。磁場分布(| H z | 2 )の透過ピークが図4c、eに示されています。これは、2つのシリコンリボンで挟まれたBIM領域がファブリペロー(FP)キャビティと見なすことができることを意味します。一次および二次共振は、FPキャビティに明確に見られます。共振周波数付近の入射プラズモン波は、FPキャビティに結合され、BIM導波路を透過して、スペクトルに透過ピークを生成します。一方、非共振周波数領域では、定在波を形成できないため、図4dに示すように、BIM導波管の左側のポートでの入射波は禁止されています。さらに、BIM導波路の分散関係と組み合わせて、結合モード理論(CMT)[17]:
によって透過強度を解析的に計算できます。 $$ T \ left(\ omega \ right)=\ frac {\ kappa_w ^ 2} {{\ left(\ omega-{\ omega} _0 \ right)} ^ 2-{\ left({\ kappa} _w + { \ kappa} _i \ right)} ^ 2}、$$(5)ここでω 0 はそれぞれFPキャビティの共振周波数です。ここで、κ w =ω 0 /(2 Q w )およびκ i =ω 0 /(2 Q i )は、それぞれFPキャビティの導波路結合損失と固有損失に関連する減衰率です。合計および固有の損失品質係数は、 Q によって推定できます。 t =ω 0 / FWHM、および Q oi =− Re( n eff )/(2Im( n eff ))、 それぞれ。次に、導波路結合損失の品質係数は、総損失から固有損失を差し引くことによって取得できます。つまり、 Q ei =Q oi Q ti /( Q oi − Q ti )[17]。図4bに示すように、CMTに基づく分析結果は、数値シミュレーションとよく一致しています。
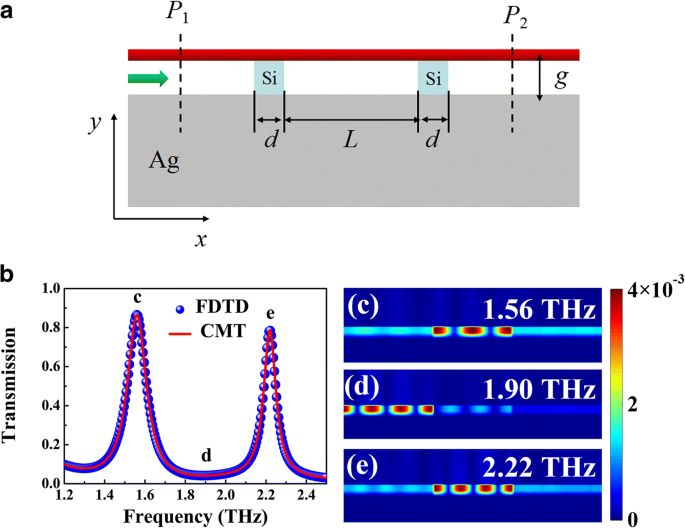
a シリコンリボンが導入されたBIM導波路の概略図。各シリコンリボンの幅は d です。 、リボン間の距離は L 。 b g である、提案された構造の数値(青いボール)およびCMT適合(赤い曲線)透過スペクトル =1μm、 d =5μm、および L =120μm。 c – e 磁場分布(| H z | 2 )の入射周波数1.56( c )、1.90( d )、および2.22 THz( e )
図5は、共振周波数のキャビティ長 L への依存性を示しています。 、ここで g =1μm、 d =5μm、および E F =70meV。 L の増加に伴い、透過ピークは赤方偏移する傾向があります。 、図5aに示すように、これは定在波共振条件2 k によってさらに説明できます。 SPP (ω r ) L +θ =2 mπ ( m =1、2、3、...)、ここでθ はシリコンと空気の界面からの反射位相シフトであり、 k SPP (ω r )は、共振周波数でのBIM導波路の波数ベクトルです。図5bに示すように、第1モードと第2モードの共振周波数は、実際に L の増加に伴って赤方偏移を示します。 。式によると。 (1)、モード制限はギャップ幅 g の影響を受けます したがって、これは共振周波数に影響を与えます。図6aは、さまざまな g の透過スペクトルを示しています。 、ここで L =120μmおよび E F =70meV。 g の増加に伴い 、同じ順序の共鳴ピークは青方偏移を示します。この現象は、Re( n の劇的な減少に起因する可能性があります。 eff )図6cに示すように。 BDSのフェルミエネルギーの調整は、実験でのアルカリ表面ドーピングによって実現できます。図6bは、さまざまなフェルミエネルギーの透過スペクトルを示しています。他のパラメータは図4bと同じです。フェルミエネルギーが増加すると、透過ピークは青方偏移を示します。これは、定在波の共鳴画像にも関係している可能性があります。固定長の場合 L 、FPキャビティは、定義されたSPP波長λの共振をサポートします。 SPP =λ 0 / Re( n eff )、ここでλ 0 は入射波長です。図6cに示すように、Re( n eff )はフェルミエネルギーの増加とともに減少します。その結果、入射波長λ 0 λを維持するには、同様に減らす必要があります SPP 定数として。これが、フェルミエネルギーの増加に伴って透過ピークが青方偏移する傾向がある理由です。一方、透過ピークの帯域幅は狭くなります。これは、Im( n の減少に起因する可能性があります。 eff )、つまり、BIM導波路におけるプラズモン導波路モードの伝搬損失。
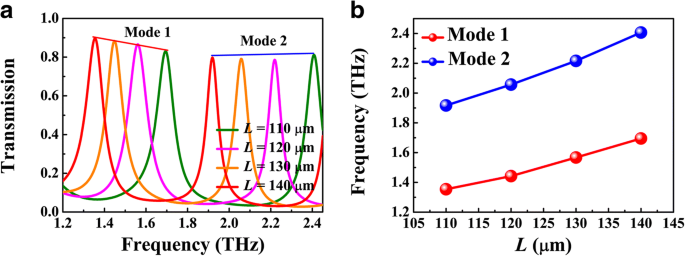
a さまざまなキャビティ長の数値透過スペクトル L 。 b キャビティ長 L の関数としてのモード1および2の共振周波数 。ここで、 g =1μm、 d =5μm、および E F =70 meV
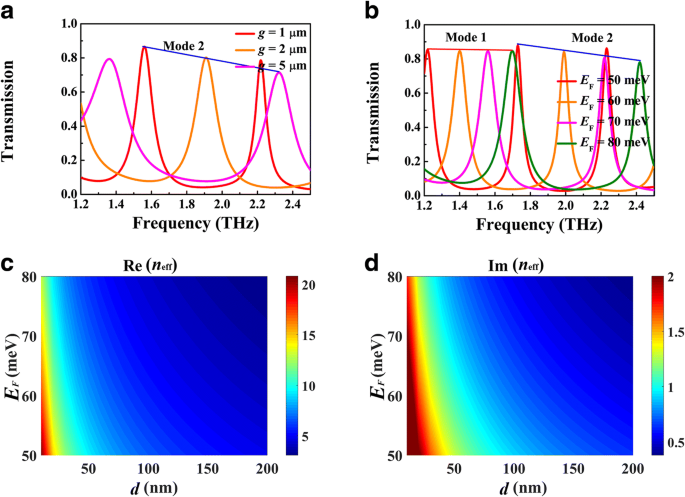
さまざまなギャップ幅の透過スペクトル g ( a )とフェルミエネルギー E F ( b )、他のパラメータは図4bと同じです。 Re( n の依存関係 eff )( c )およびIm( n eff )( d )フェルミエネルギーについて E F とギャップ幅 g
結論
要約すると、BIM導波路によってサポートされる高度に閉じ込められたテラヘルツプラズモンモードを示しました。モードの閉じ込めと損失の特性は、BDS-金属分離とフェルミエネルギーの変化で説明されています。これは、従来のSPPモードではほとんど報告されていない、モードの閉じ込めが強化され、伝搬損失が低減された最適化された周波数範囲があることを示しています。金属構造で。以前に研究されたBDSベースの構造とは異なり、このBIM導波路のモードは、幅がλよりも小さい非常に狭いスリットで効率的にサポートできます。 0 / 2000。 2つのシリコンリボンを反射鏡として使用することにより、動的に調整可能なバンドパスフィルターが実現され、構造パラメーターを再最適化することなく、BDSフィルムのフェルミエネルギーを調整することで共振周波数をアクティブに制御できます。
メソッド
数値結果は、2D有限差分時間領域(FDTD)法を使用して得られます。この方法では、 x の散乱光を吸収するように完全一致層が設定されます。 および y 方向。 BDSフィルムのメッシュサイズはd x として設定されています ×d y =1μm×0.02μmで良好な収束を実現します。
BDSの周波数依存導電率は、ランダム位相近似を使用した久保公式で記述されます[12、25]。
$$ \ operatorname {Re} \ sigma \ left(\ Omega \ right)=\ frac {e ^ 2} {\ mathrm {\ hslash}} \ frac {tk_F} {24 \ pi} \ Omega G \ left(\オメガ/ 2 \ right)、$$(3)$$ \ operatorname {Im} \ sigma \ left(\ Omega \ right)=\ frac {e ^ 2} {\ mathrm {\ hslash}} \ frac {tk_F} {24 {\ pi} ^ 2} \ left \ {\ frac {4} {\ Omega} \ left [1+ \ frac {\ pi ^ 2} {3} {\ left(\ frac {T} {E_F} \ right)} ^ 2 \ right] +8 \ Omega {\ int} _0 ^ {\ varepsilon_c} \ left [\ frac {G \ left(\ varepsilon \ right)-G \ left(\ Omega / 2 \ right) } {\ Omega ^ 2-3 {\ varepsilon} ^ 2} \ right] \ varepsilon d \ varepsilon \ right \}、$$(4)ここで G ( E )= n (− E )− n ( E )および n ( E )はフェルミディラック分布関数 E です。 F BDSのフェルミエネルギー k F = E F / ћv F はそのフェルミ運動量であり、 v F =10 6 m / sはフェルミ速度です。 ε = E / E F 、Ω=ћω/ E F +iћτ -1 / E F 、ここでћτ -1 = v F /( k F μ )は、キャリア移動度μに強く依存する電子散乱率です。 ε c = E c / E F ( E c は、ディラックスペクトルが線形でなくなるカットオフエネルギーです)、および t は量子縮退係数です。 AlCuFeを例にとると、計算のフィッティングパラメータは次のように設定されます。 t =40、ε c =3、μ= 3×10 4 cm 2 V -1 s -1 および E F =70meV。
人間の参加者、データ、組織や動物はこの研究に関与していません。
略語
- BDS:
-
バルクディラックセミメタル
- BIM:
-
BDS-絶縁体-金属
- CMT:
-
結合モード理論
- FDTD:
-
有限差分時間領域
- FWHM:
-
半値全幅
- SPP:
-
表面プラズモンポラリトン
ナノマテリアル
- テラヘルツバンド入門
- ドラッグデリバリーを強化するためのナノファイバーとフィラメント
- 局在表面プラズモン共鳴に基づく金ナノバイオセンサーは、ヒトブルセラ症を診断することができ、迅速で手頃な方法を導入します
- 偏位したトランケートされたAgナノプリズム二量体への局在表面プラズモン共鳴依存性
- グラフェン/ MnZnフェライト/ p-Siヘテロ接合の赤外線特性とテラヘルツ波変調
- 陽極TaOxナノチューブアレイの生体適合性の向上
- TiをドープしたMgAl2O4ナノリンの表面の欠陥
- メタマテリアルにおける表面プラズモンポラリトンと磁気双極子共鳴の結合効果
- 誘電体ナノプリズムに基づくプラズモンセンサー
- 二次元ハイブリッド金属ハロゲン化物デバイスは、テラヘルツ放射の制御を可能にします
- 新しい柔軟なテラヘルツカメラは、さまざまな形状のオブジェクトを検査できます



