複数の3次元トラクターカーブビームの同時生成

はじめに

ずっと前に、人々は力を発揮する光の能力を示しました。光ビームで物体を引き付けるというアイデアも、長い間私たちの注目を集めてきました。位相の特異性と独自の軌道角運動量により、光渦は、光マイクロマニピュレーション、量子通信、光イメージング、および光測定の分野で重要な研究価値を持っています[1,2,3,4,5,6]。光渦を発生させる技術が開発されており、さまざまな用途に役立つ可能性がありますが、単一の光渦の効率はまだ低いです。複数の粒子を同時に捕捉し、異なる粒子を別々に操作するために、光渦アレイの生成がホットな話題になっています[7、8]。

最近の理論的研究[9,10,11,12,13]は、トラクタービームが進行波であり、照射された物質をその長さに沿って光源に戻すことができることを示しています。レーザービーム制御の新たな進歩により、トラクタービームの実験的実現が実現しました[14、15]。 3D渦トラップの重要なタイプの1つは、光軸の周りに固定されたスパイラル形状を示す、いわゆるソレノイドビームです[16]。この曲線に沿って位相勾配を指定して、トラクタービームを得ることができます。これは、ベッセルビームの同一線上の重ね合わせにらせん相を課すことによって達成されました。 RuffnerとGrier [17]は、軸方向の波数が異なる2つの同軸ベッセルビームの干渉によって得られるトラクタービームのクラスの特性を実験的に実証および分析しました。 2013年、Rodrigo etal。設計された位相のみのホログラムを空間光変調器（SLM）にロードし、その間にSLMにレーザーを照射することにより、トラクタービームを効率的に生成する方法を紹介します。彼らはこの技術を使用して、コンピューターで生成されたホログラム（CGH）に基づいて位相と強度が規定された高強度勾配（HIG）ビームを生成できるようにしました[18]。彼らは、異なる3D形状のビームを成形できることを実験的に証明しました。 HIGと位相勾配力は、光放射圧に対しても複数の粒子を移動させることができる3Dレーザートラップの構築に不可欠です[19]。 Rodrigoはまた、HIGと位相勾配力を含むフリースタイルレーザートラップが複数の粒子を閉じ込め、それらの運動を駆動できることを示しました[20]。ただし、報告されている作業のほとんどは、単純な3Dトラクタービームの生成に焦点を合わせているため、ビーム成形のアプリケーションのさらなる開発には限界があります。上記の分析に基づいて、複数の3Dトラクタービームを生成するための高度なビーム成形技術が緊急に必要とされています。

この論文では、修正されたホログラフィックビーム成形技術を使用して複数の3Dトラクタービームを生成する方法を示します。ここでは、すべてのCGHが多重化され、それぞれの線形位相格子を追加することによって1つの位相のみのホログラムにエンコードされます。さまざまな角度でねじれた複数の3Dトラクタービームを設計します。このような新しいトラクタービームは、光渦の応用分野を拡大することが期待されており、超高性能の複数の光学応用の実現に役立つ可能性があります。

メソッド

図1aは、[18]のホログラフィック3Dビーム成形技術のスキームを示しています。これにより、強度と位相分布が所定の3D曲線に従う複雑なビームを設計できます。複素振幅フィールドを位相ホログラフィック回折格子にエンコードすることは、CGHを計算する方法です。具体的には、目的の焦点ビームを生成するために、入射面の複素振幅は次の式で与えられます。

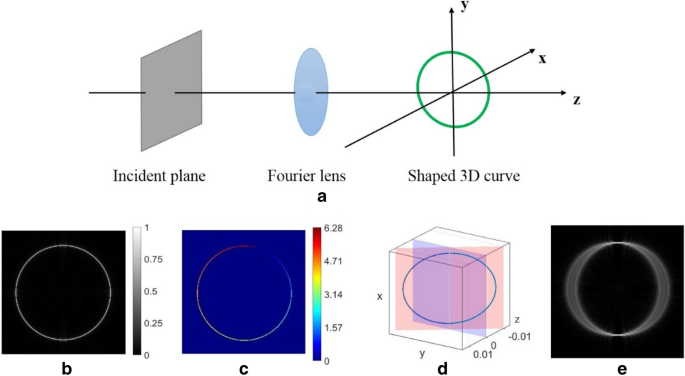
a ホログラフィック3Dビーム成形技術のスキーム。 b 、 c 焦点面での2Dリング曲線の再構成された強度と位相分布。 d 平面 z に対して傾斜したリングカーブの空間概略図 =0。 e 焦点面に焦点を合わせたリングトラクタービーム（ z =0）

用語ψ （ x 、 y 、 t ）およびφ （ x 、 y 、 t ）式で。 （1）は

[ x ₀ （ t ）、 y ₀ （ t ）、 z ₀ （ t ）]は、 t のデカルト座標で指定された3D曲線を表します ∈[0,2 π ]。 f ₀ およびλ フーリエレンズの焦点距離と波長をそれぞれ参照してください。

式（1）は、特殊な強度分布と位相勾配（曲線に沿ったらせん位相）を備えた構造的に安定した焦点ビームを形成できる入射複素フィールド（つまり、複素CGH）を計算できます。まず、2Dリングカーブ x を検討します。 ₀ （ t ）=Rcos（ t ）、 y ₀ （ t ）=Rsin（ t ）。得られたビームの強度分布を図1bに示します。リングの位相分布は、m =1のトポロジカル電荷の下で曲線に沿って明確に定義されています[図1cを参照]。図1dで傾斜したリングを考えます。リングカーブの平面は、平面 z に基づいて特定の角度に傾斜しています。 =0.この場合、ビームは焦点が合っており、上部と下部のポイントに表示されます[図1eを参照]。

焦点場で部分的に分離されたさまざまなトラクター曲線ビームを多重化するために、各複素CGHは式（1）で計算されます。 （1）固有の搬送周波数でエンコードする必要があります。これは、各ビームのホログラムに線形位相格子を追加することで実現できます。空間フィルターと組み合わせた線形回折格子は、一般に、最初の回折次数を望ましくないゼロ以上の回折次数から分離するために使用されます。線形位相格子の伝達関数は次のように与えられます

u _i および v _i は、焦点距離 f のフーリエレンズで達成された遠方場で生成されたビームの空間座標です。 ₀ 。 k =2 π / λ は波数、 z _i は、焦点面（フーリエ面）から離れる軸方向にシフトした変位です。トラクターのカーブビームを同時に生成するには、最終的な複雑なCGHの式を追加する必要があります

結果と考察

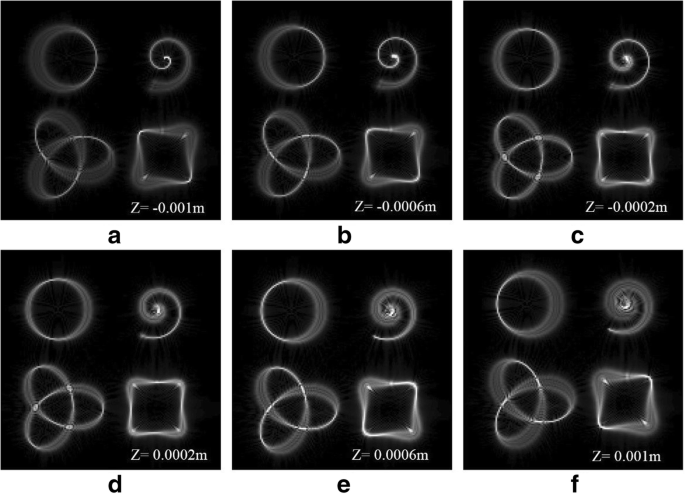
3D構成でのライトフィールド調整は、流体環境での粒子の3D操作などの実際のアプリケーションで非常に意味があります。したがって、強度と位相が異なる形状の3D曲線に沿って規定されているHIGビームの生成を研究します。具体的には、傾斜リング図2a–e、アルキメデススパイラル図2f–j、トレフォイル結び曲線図2k–o、および正方形曲線図2p–tを検討します。対応する曲線式を表1に示します。これらの3D構造は、焦点領域でのビーム伝搬に沿って明らかになります。焦点面（ z ）で測定されたビーム強度分布 =0）を図2の3列目に示します。 Z 図2の他の列に対応する座標は、シミュレーション図でマークされています。

3Dトラクタービームのシミュレーション結果。 a – e さまざまな z に焦点を合わせた3Dトラクタービームのリングカーブ プレーンズ。 f – j さまざまな z に焦点を合わせた3Dトラクタービームの代数螺旋 プレーンズ。 k – o さまざまな z に焦点を合わせた3Dトラクタービームの三つ葉結び曲線 プレーンズ。 p – t さまざまな z に焦点を合わせた3Dトラクタービームの正方形の曲線 飛行機

光学マイクロマニピュレーションの分野では、3D歪みの程度が異なるトラクタービームがアプリケーションで大きな役割を果たす可能性があります。しかしながら、より高い効率のために、異なる場所で差別化された操作を同期的に実行することが強く望まれる。したがって、4つのパターンの複数のトラクタービームを同時に設計します。各パターンを使用して、特定の粒子をある程度の3D歪みのある所定の幾何学的曲線に閉じ込めることができます。トラクタービームの相対位置を設計できます。複数のトラクタービームが3D領域に焦点を合わせていることを示すために、観察する6つの2D平面を選択しました。トラクタービームは、図3に示すように、さまざまな2D平面に焦点を合わせています。これらの3D構造は、焦点領域でのビーム伝搬に沿って明らかになります。

異なる場所での複数の3Dトラクタービームのシミュレーション結果。 a – c 焦点面の前のビームの再構成された強度。 d – f 焦点面後のビームの再構成された強度

複数の操作された粒子の相互作用を観察するために、銅のような入れ子になったグラフィックトラクタービームを設計しました。内側と外側の梁の3D歪みと形状は別々に設計できます。リングカーブは平面に焦点を合わせています（ z =0）であり、正方形の曲線にはある程度の3D歪みがあります[図4a–eを参照]。正方形の曲線は平面に焦点を合わせています（ z =0）、リング曲線にはある程度の3D歪みがあります[図4f–jを参照]。焦点面（ z ）で測定されたビーム強度分布 =0）を図4の3列目に示します。 z 図4の他の列に対応する座標は、シミュレーション図にマークされています。トラクタービームの形状を柔軟に調整して、さまざまな位置にある粒子を制御できます。

銅のような入れ子になったグラフィックトラクタービームのシミュレーション結果。 a – e 傾斜した正方形の曲線で形作られたビームは、さまざまな z に焦点を合わせます プレーンズ。 f – j 傾斜したリングカーブで成形されたビームは、さまざまな z に焦点を合わせます 飛行機

上で紹介した方法を使用して、調整可能な集束領域に複数の3Dトラクタービームを集束させる目的を達成できることを確認するために、光学実験が実施されました。図5に示すように、3Dトラクタービームを生成するための光学セットアップは、液晶空間光変調器（SLM）、4fフィルタリングシステム、およびフーリエ変換（集束）レンズで構成されています。波長532nmの固体レーザーは平面波照明にコリメートされます。 SLM（Holoeye Pluto、8ピクセルピッチ、1920×1080解像度）は、フェーズのみのCGHに対応するために使用されます。二相法[18、20]を使用して、複雑なCGH H をエンコードします。 （ x 、 y ）式によって計算されます。 （4）フェーズのみのCGHに。これは、複雑な関数をホログラムとしてSLMにエンコードすることで構成されます。次に、SLMによって変調されたビームは、フーリエ変換レンズのバックアパーチャに投影されます（ f =400 mm）4f光学フィルタリング構成を介して。電荷結合装置（CCD）カメラは、生成された強度パターンを記録するために集束レンズのフーリエ面に配置されます。 3Dトラクタービームの結果を図6に示します。結果のビームは4f光学システムを通過した後に誤差がありますが、シミュレーション結果とよく一致しています。

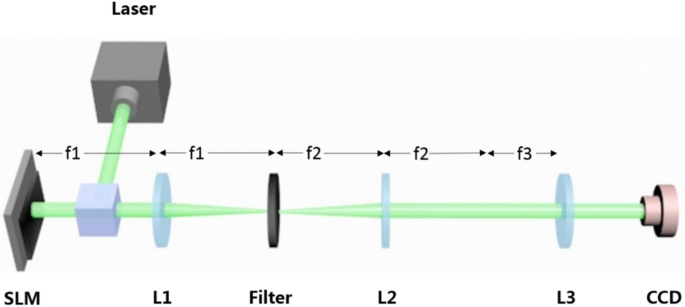
実験のセットアップ。ホログラムは、コリメートされたレーザービームによって照らされるSLMにアドレス指定されます。ビームがレンズ1を通過した後、目的のパターンを絞りでフィルタリングできます。次に、得られたビームはレンズ2とレンズ3を通過し、カメラでキャプチャできます

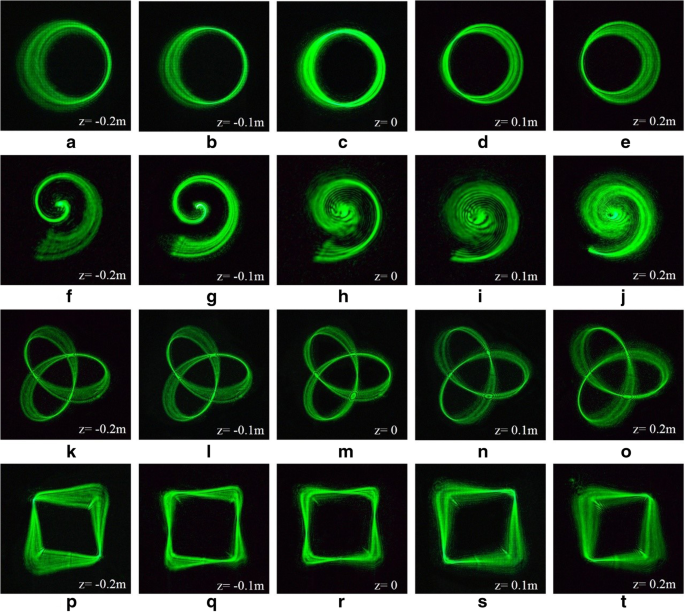
3Dトラクタービームの実験結果。 a – e さまざまな z に焦点を合わせた3Dトラクタービームのリングカーブ プレーンズ。 f – j さまざまな z に焦点を合わせた3Dトラクタービームの代数螺旋 プレーンズ。 k – o さまざまな z に焦点を合わせた3Dトラクタービームの三つ葉結び曲線 プレーンズ。 p – t さまざまな z に焦点を合わせた3Dトラクタービームの正方形の曲線 飛行機

複数の3Dトラクタービームの結果を図7に示します。シミュレーションとの比較に便利な6つの2D平面を選択して観察しました。シミュレーション結果は実験結果とよく一致しています。この方法により、複数の3Dトラクタービームを柔軟かつ効率的に生成できることが確認されています。ある程度の3D歪みのあるさまざまなビームは、粒子を閉じ込めることができます。

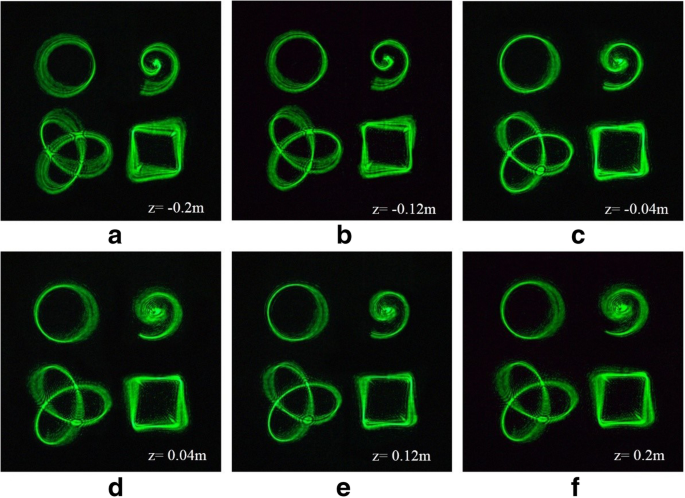
異なる場所での複数の3Dトラクタービームの実験結果。 a – c 焦点面の前のビームの再構成された強度。 d – f 焦点面後のビームの再構成された強度

銅のような入れ子になったグラフィックトラクタービームの結果を図8に示します。シミュレーション結果は実験結果とよく一致しています。したがって、2つのネストされたビームはほとんど相互作用しません。トラクタービームは、さまざまな曲線での複数粒子の操作に使用できます。

銅のような入れ子になったグラフィックトラクタービームの実験結果。 a – e 傾斜した正方形の曲線で形作られたビームは、さまざまな z に焦点を合わせます プレーンズ。 f – j 傾斜したリングカーブで成形されたビームは、さまざまな z に焦点を合わせます 飛行機

結論

空間位置を個別に調整して、複数の3Dトラクタービームを設計します。一方、個々のビームは、任意の幾何学的曲線に沿って規定され、必要に応じて任意の角度でねじれる可能性があります。理論的および実験的に、3D構成での光学式トラクタービームの生成が容易に達成できることを証明します。高強度グラジエントと位相グラジエントには、粒子を捕捉する機能があります。現在、実験が行われており、光渦ビームによる粒子の損傷は最小限に抑えられています。私たちの仕事は、トラクタービームの種類を広げます。これは、複数の光学用途向けのトラクタービームのさらなる開発に意味があり有用であると考えられています。

略語

2D：

二次元

3D：

三次元

CGH：

コンピューターで生成されたホログラム

HIG：

高強度勾配

SLM：

空間光変調器