フォトニック分子オプトメカニクスにおける制御可能な光双安定性と4光波混合

背景

機械的共振器に結合された光共振器で構成され、放射圧によって誘発されるコヒーレントな光子-フォノン相互作用を探索するオプトメカニックシステム（OMS）[1]は、機械的共振器と電磁場を操作し、フォノンレーザー[2、3]、センシング[4]、フォノンスクイーズ[5]、スクイーズド光の実現[6–8]、地上冷却[9–11]などのオプトメカニカルデバイスの潜在的なアプリケーションへの道固体デバイスでのオプトメカニカル誘導透明度（OMIT）[12–15]誘導ストアライト[16、17]。単一のOMSに最も注意が払われていますが、放射圧を介して2つの光学モードに結合された1つの機械モード[18、19]や2つの機械共振器間のフォノニック相互作用[20]など、より多くの光学モードまたは機械モードを統合することによって複合OMSを実現します。 、21]は、量子情報処理におけるOMSとその潜在的なアプリケーションをさらに調査する傾向になります。ハイブリッド化合物OMSに基づいて、量子状態の伝達[22]、OMITのようなフォノン冷却[23]、オプトメカニカルダークモード[24]、およびフォノンを介した電磁誘導吸収[25]が広く研究されています。多数の化合物OMSでは、一般的なOMSの自然な拡張として、1つのWGMマイクロキャビティでオプトメカニカル効果を持つフォトニック分子[26、27]と呼ばれる2つの直接結合ささやき回廊モード（WGM）マイクロキャビティが大きな注目を集めています。複合フォトニック分子オプトメカニカルシステムには2種類の相互作用があります。1つは放射圧によって誘発されるオプトメカニカル相互作用であり、もう1つは調整可能な光子トンネリングを介したキャビティ-キャビティ結合です。 2つの相互作用が一緒になって、フォノンレイジング[2、3]、カオス[28]、基底状態冷却[23]、光透過のコヒーレント制御[25、29、30]などのいくつかの興味深い現象が発生します。

一方、OMSは、光と物質の相互作用の非線形効果を調査するためのプラットフォームも提供します。 OMSのすべての非線形現象の中で、光双安定性と4光波混合（FWM）は、研究者の関心に焦点を当てた典型的な非線形光学現象です。近年、平均空洞内光子数の双安定挙動が、ボーズ・アインシュタイン凝縮空洞オプトメカニカルシステム[31、32]、量子井戸を備えたOMS [33]、極低温原子[34、 35]、および他のハイブリッドOMS [36、37]。さらに、FWMは、周波数ωの強力なポンプレーザーによって駆動されるキャビティとして説明できます。 _p 弱いプローブレーザー周波数ω _s 、次に、2つのポンプ光子が機械的モードを介してプローブ光子と混合し、周波数2 ωのアイドラー光子を生成します。 _p − ω _s OMSで研究されており、強結合オプトメカニカルシステムでのモード分割[38]、コヒーレント機械駆動OMS [39、40]、2モードキャビティオプトメカニカルシステム[41]などの以前の研究でも調査されています。ただし、光双安定性とFWMは、 J で表される結合強度を持つ複合フォトニック分子OMSではほとんど研究されていません。 2つの空洞のうちの1つは、これらの非線形光学現象に影響を与える重要な役割を果たします。

本研究では、2つのWGMマイクロキャビティで構成される複合フォトニック分子キャビティオプトメカニカルシステムを検討します。1つのWGMキャビティは、キャビティ散逸の大きいオプトメカニカルキャビティですκ 、およびもう1つのWGMキャビティは、高品質係数（Q）を備えた補助的な通常の光共振器です[42]。 Liuらのように。 [43]実証されているように、同じタイプの共振器で高いQファクターと小さなモードボリューム（V）を同時に達成することは依然として困難です。フォトニック分子オプトメカニクスでは、元々のオプトメカニカルキャビティを結合することにより c 高キャビティ散逸κ （高Qなし）補助キャビティモード a Qが高いがVが大きい場合、同じキャビティのQが高くVが小さいという要件を取り除くことができます。比率パラメータδを導入します =κ _c / κ _a 、ここでκ _c =ω _c / Q _c およびκ _a =ω _a / Q _a キャビティモードの減衰率です c および a （ω _c およびω _a 空洞の周波数です c および a ）フォトニック分子オプトメカニクスにおける非線形効果を調査する。ここでは、オプトメカニカルキャビティ c 補助キャビティ a がポンプレーザーによって駆動されている間、 プローブレーザーによって駆動されます。空洞 c キャビティ a に結合されています エバネッセント場を介して、および結合強度 J 2つのWGMキャビティ間の間隔を変えることにより、2つのキャビティ間の間隔を制御できます[26]。結合強度 J を変化させることにより、複合フォトニック分子OMSに基づく光双安定性とFWMを調査します。 空洞共振器間、および調整可能で制御可能な光双安定性とFWMは、結合強度 J を操作することで実現できます。 2つの空洞の間。さらに、パラメータδを調整すると とポンプパワー P 、FWMプロセスを制御できます。

モデルと理論

フォトニック分子オプトメカニクスを図1に示します。最初のキャビティは光学モード c をサポートします。 周波数ω _c 周波数ωのポンプレーザーによって駆動 _p 振幅\（\ varepsilon _ {p} =\ sqrt {P / \ hbar \ omega _ {p}} \）。放射圧は機械的モードを誘発します b 機械的共振器周波数ω _m 、および単一光子オプトメカニカル結合率は g です。 = g ₀ x ₀ （ g ₀ =ω _c / R および R はキャビティの半径 c ）、機械振動子の位置のゼロ点変動は\（x_ {0} =\ sqrt {\ hbar / 2M \ omega _ {m}} \）[13]です。次に、オプトメカニクスのハミルトニアン c は[13]

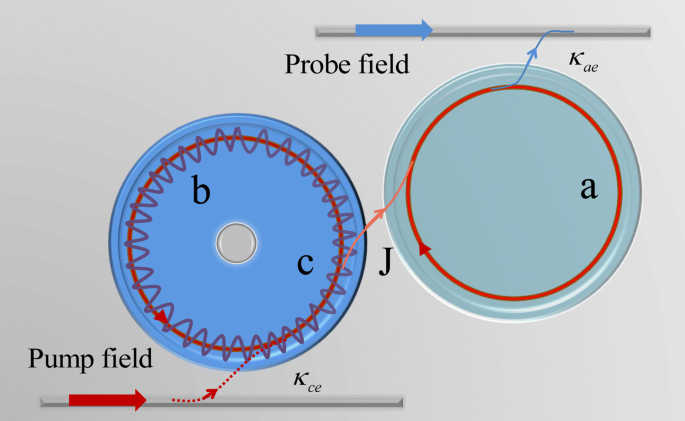
2つのWGMキャビティを含む複合フォトニック分子キャビティオプトメカニカルシステムの概略図。高キャビティ散逸を備えた最初のWGMキャビティκ オプトメカニカルキャビティ c ポンプレーザーによって駆動され、放射圧が機械的モードを誘発します b キャビティへの結合 c 結合強度 g 。 2番目のWGMキャビティ a は、高品質係数（Q）のプローブレーザーによって駆動される補助キャビティです。オプトメカニカルキャビティ c キャビティ a に結合されています エバネッセント場を介して、パラメータ J を導入します 2つの空洞の結合強度を説明します。結合強度は、2つの空洞間の間隔を変えることで制御できます[26]

ここで、Δ _c =ω _c − ω _p ポンプ場とキャビティの離調です c 。 c および c ^† 空洞モード c のボソン消滅および生成演算子を表す 、および b ^† （ b ）は、機械モードの生成（消滅）演算子です。補助キャビティは、光学モード a のみをサポートします 周波数ωのプローブレーザーによって駆動 _s 、およびその振幅ε _s は\（\ varepsilon _ {s} =\ sqrt {P_ {s} / \ hbar \ omega _ {s}} \）です。消滅および生成演算子 a を紹介します および a ^† 空洞を説明する a 、およびそのハミルトニアンは[13]

ここで、Δ _a =ω _a − ω _p ポンプフィールドとキャビティの離調です a 、およびΩ =ω _s − ω _p ポンププローブの離調です。 2本のテーパーファイバーを使用してキャビティモードを励起します a およびキャビティモード c 結合率κの光導波路として _ae およびκ _ce 。オプトメカニカルキャビティ c 空洞に結合する a エバネッセント場を介して、およびキャビティ-キャビティ結合率 J それらの間の距離を変えることによって効率的に調整することができます[26]。結合強度 J 2つの空洞の間で弱い場合、空洞からのエネルギー c 空洞に簡単に移動できない a 。逆に、結合強度 J 2つの空洞間の距離が短くなると増加し、エネルギーは2つの空洞から簡単に流れることができます。 2つの空洞間の線形結合相互作用は、[26] \（\ hbar J \ left（a ^ {\ dag} c + ac ^ {\ dag} \ right）\）で表されます。次に、ポンプ周波数ωの回転波フレーム内の全ハミルトニアン _c 書くことができます[3、13、23]

2つのキャビティモードの減衰率κ =κ _c =κ _a =κ _ex + κ ₀ 固有の光子損失率κ ₀ 、およびκ _ex エネルギーが光共振器を離れて伝搬場に入る速度を説明します[13]。ここでは、簡単にするために、κの条件のみを考慮します。 _ex =κ ₀ =κ _ae =κ _ce 、そしてωを考慮します _c =ω _a 。

ハイゼンベルク運動方程式\（i \ hbar \ partial _ {t} O =[O、H] \）（ O を使用します = a 、 c 、 X ）そして対応する減衰演算子とノイズ演算子を導入すると、次のように量子ランジュバン方程式が得られます[44]：

ここで X = b ^† + b は位置演算子であり、γ _m は共振器の減衰率です。 a _in および c _in ランゲビンノイズの説明は、関係[45]

共振器モードは、次の相関関数を使用した確率力過程の影響を受けます[46]

ここで k _B はボルツマン定数であり、 T リザーバー温度を示します。

オプトメカニカルキャビティ c 強力なポンプレーザーによって駆動される場合、ハイゼンベルグ演算子は2つの部分に分割できます。つまり、定常状態の平均値 O ₀ 、および小さな変動δ O 平均値がゼロの場合<δ O 〉 =0。定常状態の値は、キャビティ内のフォトン数（ n ）を決定します。 _a =| a _s | ² および n _c =| c _s | ² ）

ここで、\（\ Delta ^ {^ {\ prime}} =\ Delta _ {c} -2g ^ {2} n_ {c} / \ omega _ {m} \）。この形式の連立方程式は、光双安定性の特徴です。次のセクションでは、ポンプ出力 P などのパラメータについて説明します。 、キャビティ-キャビティ結合強度 J 、および比率パラメータδ 光双安定性に影響を与えます。変動演算子の線形項のみを保持し、仮説を作成する[47] 〈δ a 〉 = a ₊ e ^{− i Ω t} + a ₋ e ^{i Ω t} 、〈δ c 〉 = c ₊ e ^{− i Ω t} + c ₋ e ^{i Ω t} 、〈δ X 〉 = X ₊ e ^{− i Ω t} + X ₋ e ^{i Ω t} 、次に

ここで、\（\ Lambda _ {1} =igc_ {s} ^ {2} \ eta ^ {\ ast} J ^ {2} \ varepsilon _ {s} \ sqrt {\ kappa _ {ae}} \）、Λ ₂ =（ i Δ _{a 2} + κ _a ）（ i Δ ₂ + κ _c ）[（ i Δ ₁ − κ _c ）（ i Δ _{a 1} − κ _a ）− J ² ]、\（\ Lambda _ {3} =-g ^ {2} \ eta ^ {\ ast 2} n_ {c} ^ {2}（i \ Delta _ {a1}-\ kappa _ {a}）（ i \ Delta _ {a2} + \ kappa _ {a}）\）、Δ _{a 1} =Δ _a − Ω 、Δ _{a 2} =Δ _a + Ω 、\（\ Delta _ {1} =\ Delta ^ {^ {\ prime}}-\ Omega + g \ eta n_ {c} \）、\（\ Delta _ {2} =\ Delta ^ {^ {\プライム}} + \ Omega + g \ eta ^ {\ ast} n_ {c} \）、および\（\ eta =2g \ omega _ {m} /（\ omega _ {m} ^ {2} -i \ガンマ_ {m} \ Omega- \ Omega ^ {2}）\）。標準の入出力関係を使用する[45] \（a _ {\ text {out}}（t）=a _ {\ text {in}}（t）-\ sqrt {2 \ kappa _ {a}} a（t ）\）、ここで a _out （ t ）は出力フィールド演算子であり、出力フィールドの期待値を取得します。

ここで a _out （ t ）は出力フィールド演算子です。式（13）は、出力フィールドが3つの項で構成されていることを示しています。最初の項は、振幅εの駆動フィールドでの出力フィールドに対応します。 _p と周波数ω _p 。第2項は、周波数ωのプローブフィールドに対応します。 _s さまざまなオプトメカニカルシステムで調査されているOMITをもたらす反ストークス分野に関連しています[12–15、48]。最後の1つは、周波数2 ωの出力フィールドに対応します。 _p − ω _s FWMを表示するストークフィールドに関連します。 FWMプロセスでは、駆動フィールドの2つの光子が、それぞれ周波数ωのプローブフィールドの1つの光子と相互作用します。 _p およびω _s 周波数2の新しい光子が生まれたω _p − ω _s 。プローブフィールドに関するFWM強度は、[49]

これはオプトメカニカル結合強度 g によって決定されます 、ポンプ出力 P 、キャビティ-キャビティ結合強度 J 、および減衰率比δ 2つの空洞の。

数値結果と考察

このセクションでは、最初に定常状態の光子数 n の双安定挙動を調査します。 _c および n _a 式による2つの空洞の。 （10）と（11）。双安定条件を分析的に表現するのは面倒なので、ここでは数値結果を示します。参考文献と同様のパラメータを選択します。 [13、26]：キャビティ c のパラメータ [13]として： g ₀ =12 GHz / nm、γ _m =41 kHz、ω _m =51.8 MHz、κ _c =5 MHz、 m =20 ng、λ =750 nm、および Q =1500であり、ポンプ電力の大きさのオーダーはミリワット（1 mW =10 ^-3 ）です。 W）。キャビティ a の場合 、ωを検討します _a =ω _c およびκ _c =κ _a 。結合強度 J 2つのキャビティモード間が重要な役割を果たし、双安定動作とFWMに影響を与える可能性があります。結合強度 J が実験的に報告されています キャビティ間の距離に依存します c と空洞 a [26]（2つのキャビティの距離が長くなると、結合強度も指数関数的に減少します）。ここでは、結合強度\（J \ sim \ sqrt {\ kappa _ {c} \ kappa _ {a}} \）。

オプトメカニカルキャビティのキャビティ内光子数を与える式（10）および（11） c および通常の空洞 a 双安定動作を示す結合された3次方程式です。まず、 J の状態を考えます。 =0、つまり、単一のオプトメカニカルキャビティ c 、および図2aは、キャビティ内の平均光子数 n をプロットしています。 _c オプトメカニカルキャビティの c キャビティポンプの離調Δの関数として _c =ω _c − ω _p 3つのポンプ力で。ポンプ出力が P 未満の場合 =0.4 mW（ P など =0.1 mW）、曲線はほぼローレンツです。パワーを上げると P 臨界値まで、オプトメカニカルキャビティ c P の曲線に示されているように、双安定動作を示します =0.4mWから P =0.8 mW、最初はローレンツ共鳴曲線が非対称になります。キャビティ内の平均光子数 n _c には3つの実根があり（式（10））、最大と最小の根は安定しており、真ん中の根は不安定です。これは図2aの楕円形で表されています。ただし、光共振器を考慮すると a 、つまり J J などの≠0 =1.0 κ _a 、図2bに示すように、双安定動作はいくつかの方法で壊れています。これは、オプトメカニカルキャビティ c 光共振器に結合 a 、キャビティ内フォトン番号の一部 n _c オプトメカニカルキャビティの c 光共振器に結合されます a 、したがって、キャビティ内の光子数 n _c 減少し、双安定動作が破壊されます。図2cは、キャビティ内の平均光子数 n を示しています。 _c オプトメカニカルキャビティの c キャビティ-キャビティ結合強度の関数として J 3つのポンプ力で。明らかに、平均キャビティ内光子数 n _c ポンプ出力に依存します P 、およびキャビティ内の光子数 n _c 結合強度の増加とともに常に減少します J 光子数の一部が光共振器に結合されているため a 。さらに、より大きなキャビティポンプの離調は、ポンプパワーの増加に伴う光学双安定挙動を観察するのに有益です P 。図2dは、キャビティ内の平均光子数 n をプロットしたものです。 _c 対ポンプ出力 P 空洞付き a 赤い側波帯で（Δ _a =ω _m ）および青色の側波帯（Δ _a =− ω _m ）、それぞれ、双安定性はヒステリシスループの動作を示します[50]。ただし、私たちの結果は、キャビティとキャビティの結合を考慮しない2モードオプトメカニカルシステムの以前の作業とは異なります J 。したがって、結合強度 J 双安定性において重要な役割を果たします。

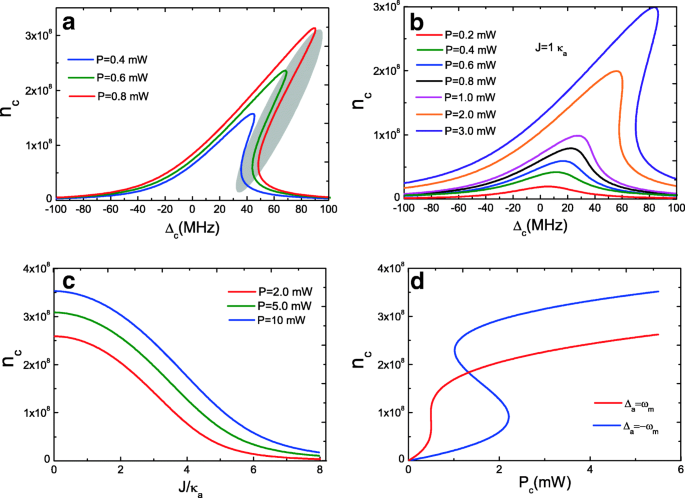
a オプトメカニカルキャビティの平均キャビティ内光子数 c キャビティポンプの離調Δの関数として _c J で3つのポンプパワーを使用 =0。 b オプトメカニカルキャビティの平均キャビティ内光子数 c キャビティポンプの離調Δの関数として _c J の下でいくつかの異なるポンプパワーで =1.0 κ _a 。 c 平均キャビティ内光子数 n _c オプトメカニカルキャビティの c J の関数として 3つのポンプ力で。 d 平均キャビティ内光子数 n _c P の関数として Δの場合 _c =Δ _a =ω _m

光共振器の双安定挙動をさらに調査します a 式で（11）。図3aは、キャビティ内の光子数 n を示しています。 _a 通常の空洞の a キャビティポンプの離調Δの関数として _a =ω _a − ω _p ポンプパワー付き P =0.1 mW、 P =1.0 mW、および P = J で10mW =1.0 κ _a 。光共振器 a キャビティ内の光子数 n のため、双安定動作として動作できません _a 空洞の a 空洞から c 低ポンプパワーでは双安定性を維持できません。実際には、高ポンプパワー P のみ むし歯 a 高ポンプパワー駆動のオプトメカニカルキャビティ c のみであるため、双安定動作を示します。 、はるかに多くの光子数が光共振器に結合できます a 。また、キャビティ内の平均光子数 n もプロットします。 _a 光共振器の a 結合強度の関数として J 図3bに示すように、3つのポンプ出力で。 J =0、 n _a =0、 J の2つのキャビティ間に結合がないため =0であり、この状態では、光子は光共振器に結合しません a 。結合強度を上げると J （2つの空洞の距離を短くする[26]）、空洞内の光子数 n _a 通常の光共振器の a 増加しますが、常にではありません。最適な結合強度があります J n の最大値 _a 異なるポンプパワーの下で、そして n _a J の増加とともに減少します 。結合強度 J であることは注目に値する事実です。 2つの空洞の間を調整することができます[26]。

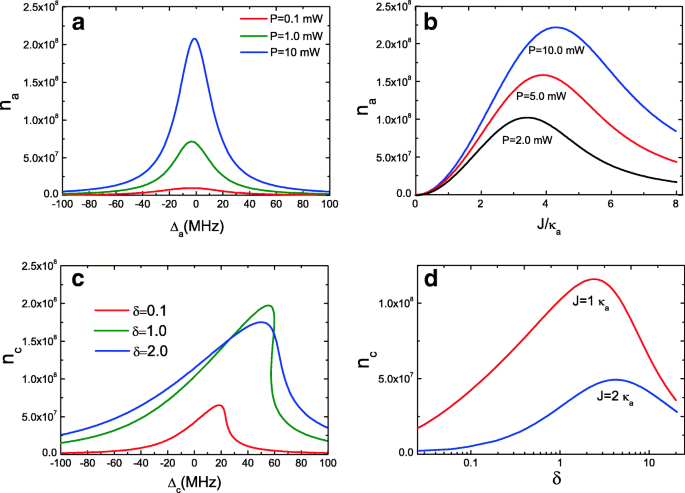
a 通常の空洞の平均空洞内光子数 a キャビティポンプの離調Δの関数として _a J で3つのポンプパワーを使用 =1.0 κ _a 。 b 平均キャビティ内光子数 n _a J の関数として 3つのポンプ力で。 c 平均キャビティ内光子数 n _c Δの関数として _c 3つの比率パラメータδ 。 d 平均キャビティ内光子数 n _c δの関数として 2つの J

さらに、比率パラメーターδを検討します。 =κ _c / κ _a （κ _c =ω _c / Q _c およびκ _a =ω _a / Q _a ）双安定動作に影響を与える2つのキャビティのパラメータを調査します。 κ はキャビティモードの減衰率であり、キャビティの周波数と品質係数に関連しています。ご存知のように、回折限界のため、キャビティモードで高いQと小さなVを同時に達成することは困難です。光共振器の場合、放射減衰率が大きいほどVが小さいほど、Qが低くなります。さまざまなタイプの共振器には独自の特性がありますが、Qが高い場合とVが小さい場合の重みは依然として存在します。ただし、元のOMS c を結合する場合 補助キャビティモードへの高キャビティ散逸 a Qは高いがVが大きい場合、双安定動作は大幅に変化します。図3cは、キャビティ内の平均光子数 n を示しています。 _c オプトメカニカルキャビティの c Δの関数として _a いくつかの異なるδの下で =κ _c / κ _a 結合強度を変更せずに J =1.0 κ _a 。双安定動作が現れる可能性があることがわかりますが、キャビティ内の光子数 n _c δでは小さい =0.1、 J =2 κ _a 、つまりκ _c =0.1 κ _a これは Q を意味します _c > Q _a 。比率を増やす場合δ δから =1.0からδ =2.0、キャビティ内の光子数 n _c 双安定動作からほぼローレンツラインプロファイルへの変化を経験します。つまり、 Q _c < Q _a 、双安定動作は壊れますが、最適な条件があります。つまり、 Q _c = Q _a 。図3dでは、キャビティ内の光子数 n を示しています。 _c δの関数として 2つの異なる J 、そして明らかに、比率パラメータδを増やすことで 、キャビティ内の光子数 n _c 増加。特定の J の最適値に達したとき 、次に n _c 下降。したがって、減衰率κなどのキャビティパラメータを制御します。 またはキャビティの品質係数、双安定動作を制御できます。

一方、典型的な非線形光学現象として、式（1）を用いてFWMプロセスも調べます。 （14）フォトニック分子オプトメカニカルシステム。図4は、FWMスペクトルをプローブキャビティ a の関数としてプロットしたものです。 Δの離調 _s =ω _s − ω _a Δで _a =Δ _c 異なるパラメータレジームの下で=0。図4a–dは、さまざまなポンプパワー P でのFWMスペクトルの変化を示しています。 J で =1.0 κ _a 。 FWMスペクトルに3つのピークがあり、Δの近くにローレンツのピークがあることは明らかです。 _s =0および2つのモード分割ピークは±ωにあります _m 、およびFWM強度は、ポンプ出力の増加とともに減少します。図4e–hは、 J からのFWMスペクトルの変化を示しています。 =0.5 κ _a J へ =2.0 κ _a ポンプ出力 P =1.0mW。結合強度を上げると J J から =0.5 κ _a J へ =2.0 κ _a 、FWMスペクトルが大幅に変化します。この現象は、単一空洞のオプトメカニカルシステムで実証されたドレス状態の画像で説明できます[51]。

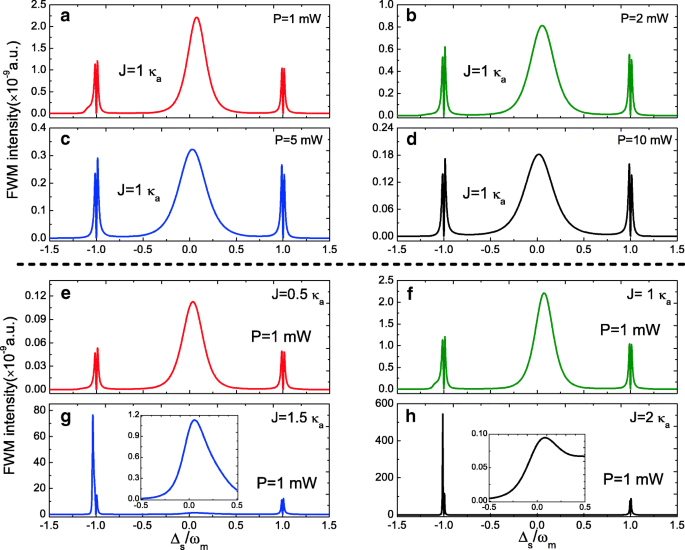
a – d 正規化されたプローブポンプ離調の関数としてのFWM強度Δ _s J でのさまざまなポンプ出力の場合 =1.0 κ _a 。 e – h Δの関数としてのFWM強度 _s さまざまな J ポンプ出力 P =1.0 mW

次に、ΔでのFWMスペクトルを調査します。 _a =Δ _c ≠0。図5a〜dは、赤い側波帯でのFWMスペクトル、つまりΔを示しています。 _a =Δ _c =ω _m 変更されていない J =1.0 κ _a P からポンプ出力を上げると =1.0から P =10mW。 2つのノーマルモード分割ピークが、±ωにあるFWMスペクトルに現れます。 _m それぞれ、FWM強度はポンプ出力の増加とともに減少します。図5e–hは、赤い側波帯、つまりΔでのFWMスペクトルを示しています。 _a =Δ _c =ω _m 固定ポンプ出力 P =2.0 mW、結合強度の増加 J J から =0.5 κ _a J へ =2.0 κ _a 。明らかに、FWM強度は、結合強度 J の増加とともに増加します。 、およびより大きな J 光共振器に結合されたより多くの光子数を意味します a 。離調を変更する場合Δ _a およびΔ _c 赤い側波帯から青い側波帯へ、つまりΔ _a =Δ _c =− ω _m 、FWMスペクトルの変化は顕著に変化します。図5i–lは、4つの異なるポンプパワーでの青色の側波帯でのFWMスペクトルを示しています。また、青色の側波帯でもポンプパワーを上げるとFWM強度が低下します。 ±ωにある2つのノーマルモード分割ピークを除く _m 、FWMスペクトルに2つの鋭い側波帯ピークが現れ、それらの位置はポンプパワーに関連しています。図5m–pでは、結合強度 J についても説明しています。 青い側波帯の下のFWMスペクトルに影響を与えます。他の鋭い側波帯ピークがFWMスペクトルに現れるかどうかは、結合強度 J に依存します。 。

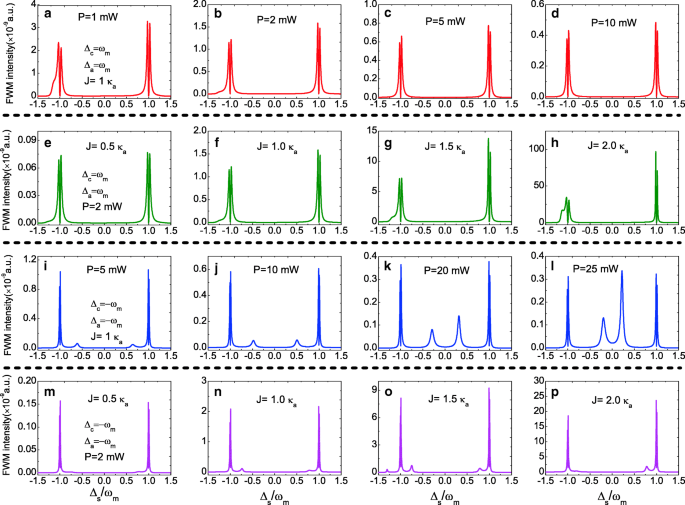
a – d Δの関数としてのFWM強度 _s さまざまなポンプ出力の場合 P 赤い側波帯で（Δ _c =Δ _a =ω _m ）および J =1.0 κ _a 。 e – h Δの関数としてのFWM強度 _s さまざまな J 赤い側波帯とポンプパワーの下で P =2.0mW。 i – l Δの関数としてのFWM強度 _s さまざまなポンプ出力の場合 P 青い側波帯で（Δ _c =Δ _a =− ω _m ）および J =1.0 κ _a 。 m – p Δの関数としてのFWM強度 _s さまざまな J 青い側波帯とポンプパワーの下で P =2.0 mW

さらに、比率パラメータδ =κ _c / κ _a 複合フォトニック分子OMSのキャビティ内光子数に影響を与える可能性がある場合、FWMスペクトルはパラメータδを制御して操作できます。 。図6a–hは、変更されていないパラメータ J でのFWMスペクトルを示しています。 =2.0 κ _a および P =比率δを増やしながら、赤い側波帯の下で10 mW δから =0.05からδ =3.0であり、FWM強度は比率δの増加とともに減少します。 。青い側波帯にある間、図6i–pに示すように、他の鋭い側波帯のピークがFWMスペクトルに現れ、比δの増加に伴ってFWM強度も減少します。 。したがって、減衰率κなどのキャビティパラメータを制御すると、 または空洞のQの場合、FWMは複合フォトニック分子OMSで簡単に実現できます。

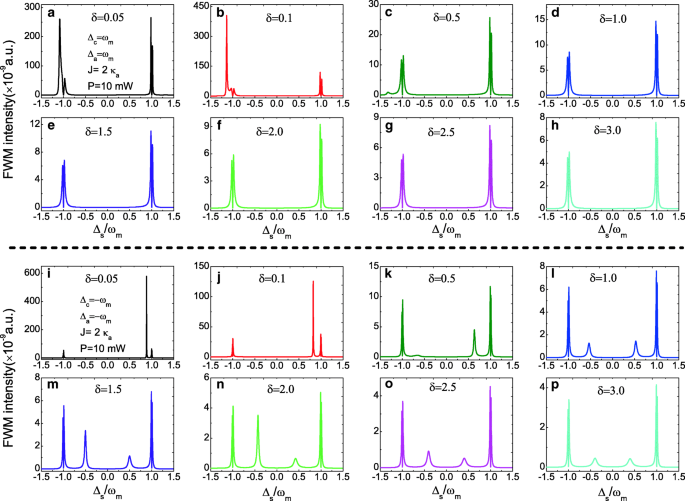
a – h Δの関数としてのFWM強度 _s いくつかの異なる比率パラメータの場合δ 赤い側波帯で（Δ _c =Δ _a =ω _m ）および J =2.0 κ _a 、 P =10mW。 i – p Δの関数としてのFWM強度 _s いくつかの異なる比率パラメータの場合δ 青い側波帯で（Δ _c =Δ _a =− ω _m ）および J =2.0 κ _a 、 P =10 mW

結論

複合WGMキャビティフォトニック分子オプトメカニカルシステムにおける光双安定性と4光波混合を調査しました。これには、高品質係数の補助キャビティに結合された高キャビティ散逸のオプトメカニカルキャビティが含まれます。結合強度 J などのさまざまなパラメータレジームの下での光双安定性を調査します。 2つの空洞と崩壊率比δの間 システム内の2つのキャビティの。光双安定性は、オプトメカニカルキャビティを駆動するポンプフィールドによって調整でき、2つのキャビティのキャビティ内光子数は結合強度 J によって決定されます。 。さらに、さまざまな駆動条件（赤の側波帯と青の側波帯）およびさまざまなパラメーター条件（結合強度 J ）の下で、フォトニック分子オプトメカニカルシステムのFWMプロセスを制御する方法も示しました。 と比率δ ）。数値結果は、FWMプロセスがそのようなパラメータで制御できることを示しています。これらの結果は、複合フォトニック分子オプトメカニカルシステムの非線形現象をよりよく理解するのに役立ちます。

略語

C-OMS：

キャビティオプトメカニクスシステム

FWM：

4光波混合

OMS：

オプトメカニクスシステム

省略：

光学機械的に誘発された透明性

Q：

品質

V：

ボリューム

WGM：

ささやきの回廊モード