グラフェン/金属系でプラズモン的に誘発された完全な吸収

背景

プラズモニクスは、その並外れた特性[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]と、統合を含む多くの分野での大きな可能性により、広く注目されています。フォトニクス、バイオセンシング、エネルギーキャプチャ、光検出。最近、スプーフィング表面プラズモン（SSP）として知られる新しいプラズモン現象が観察されました。これは、穴あき金属を介して伝播し、回折限界を克服することができます[16]。次に、SSPがTHz、マイクロ波、および低周波数範囲で調査され[17、18、19]、SSPに基づく多くの深サブ波長デバイスが提案されて実証されています[20、21]。ただし、このようなデバイスのアプリケーションは、SPPの高い減衰率によって深刻に妨げられています。この問題の解決策の1つは、人工プラズモン誘起透明度（PIT）媒体[22]です。これは、広い吸収スペクトル内でシャープな透明度ウィンドウを備えています。 PIT効果は、主に放射要素とサブ放射要素の結合に依存しており、これは広く研究されています[23、24、25]。同様の現象であるプラズモン誘導吸収（PIA）も最近実証されており、これは明るいプラズモンモードと暗いプラズモンモードの建設的な干渉に起因します[26]。 PIA共鳴[27、28]は、非常に高速な光効果を示す可能性があり、光スイッチングおよび処理に応用できる可能性があります。

しかし、金属構造のPIA効果に基づく従来のデバイスは、調整可能性を得ることが困難または不可能であり、その用途を大幅に制限します。半金属性、高い移動度、および高い調整可能性で知られるグラフェン[29、30]は、調整可能な赤外線プラズモンデバイスの優れた候補材料になり得ます。この論文では、周期的な銀の溝と単層グラフェンによってそれぞれサポートされるF-P共鳴モードと準ガイドモードの建設的な干渉によって達成される調整可能なPIA効果を調査しました。共振強度と線幅は結合距離に強く依存することがわかります。また、消光率は〜99.999％に達する可能性があることも示されています。消光比は1- R として定義されます - T 、ここで R および T それぞれ反射率と透過率です。単純に1- R ここでの透過率は0であるため、このシステムでは10 ⁶ という超高FOM *になります。 グラフェン/金属システムでは、グラフェンのゲート電圧を調整することにより、共振周波数を動的に調整できます。これらの卓越した特性は、生化学的センシングと動的な光スイッチングに適用できます。

メソッド

単層グラフェンとAl ₂ からなる構造の概​​略図を図1に示します。 O ₃ 溝のある銀の上に孤立した層。 Al ₂ の厚さ O ₃ g です 。システムは、横磁気（TM）偏波の垂直入射平面波によって照らされます。その他の構造パラメータは次のように表されます： d 銀の溝の深さです。 w 銀の溝の幅です。 P ユニットセルの周期です。中赤外領域では、高濃度にドープされたグラフェンではバンド内散乱が支配的であり、その導電率はDrudeのような形をとりますσ _g = ie ² E _F / [πħ ² （ω + iτ ^-1 ）]。電子緩和時間はτで表されます。 =μE _F / eυ _F ² 、ここでυ _F = c / 300はフェルミ速度、 E _F はフェルミエネルギーとμです =10 m ² / Vsは、グラフェンのDC移動度です[25、31、32]。有限差分時間領域（FDTD）シミュレーションでは、銀の光学定数、およびAl ₂ O ₃ 参考文献からです。 [33]およびref。 [34]。周期境界条件は、無限の周期セル構造をシミュレートするために使用されます。簡単にするために、グラフェン層の上の領域の材料は真空（ε）であると仮定します。 ₀ =1）。

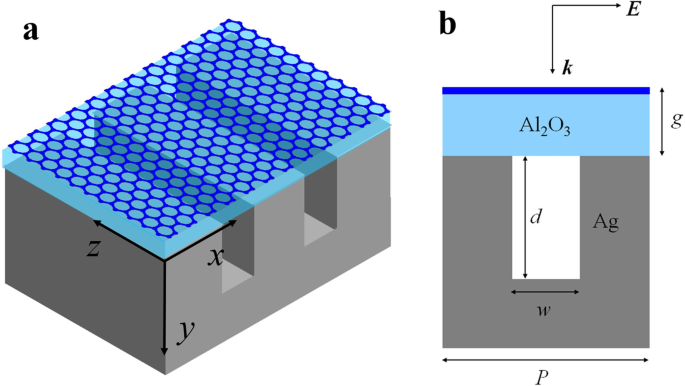
グラフェン-銀溝構造の概略図。 a 斜投影。 b ユニットセルの断面図

結果と考察

w を使用して、銀の溝の反射スペクトルをシミュレートしました。 =100 nm、 P =250 nm、 d =2000 nmであり、結果を図2a（赤い曲線）に示します。 〜28 THzで広いディップが観察され、消光比は〜44％、 Q 係数〜0.8。これは、入射光によって励起されたSSPによって誘発されたF-P共鳴によるものです[19]。この共鳴には広範囲の共鳴帯域があるため、共鳴モードはPIAシステムの超放射モードとして機能します。次に、シミュレーション領域の下部にある金属境界条件を使用して、フェルミ準位 E を使用してグラフェンシートの反射スペクトルを計算しました。 _F =0.3 eV、図2a（青い曲線）に示すように。反射スペクトルは、グラフェンプラズモン共鳴がこの周波数での入射によって直接励起されないことを示しています。グラフェンでサポートされているプラ​​ズモンモードを視覚化して最適化するために、最初にグラフェンでサポートされている共鳴モードをシミュレートします。銀の溝のF-P共振の潜在的な影響を排除するために、溝が銀ではなくシリコンでできていると仮定します。構造の反射スペクトルは、 E について計算されました。 _F =0.3eVおよび異なるユニットセル P 図2bに示されています。共振周波数での反射率の低下 f =32.84THzは P で観測できます =250 nm、 Q 係数〜304。高い Q 狭い共鳴帯域での共鳴は、PIAシステムのサブラジアント（ダーク）モードとして機能します。反射率の低下は、グラフェンのプラズモン準ガイドモードと法線入射の共鳴によるものです[35]。これは、溝が m に基づいて波数ベクトルの不一致を補正できるためです。 3次位相整合条件[36、37]

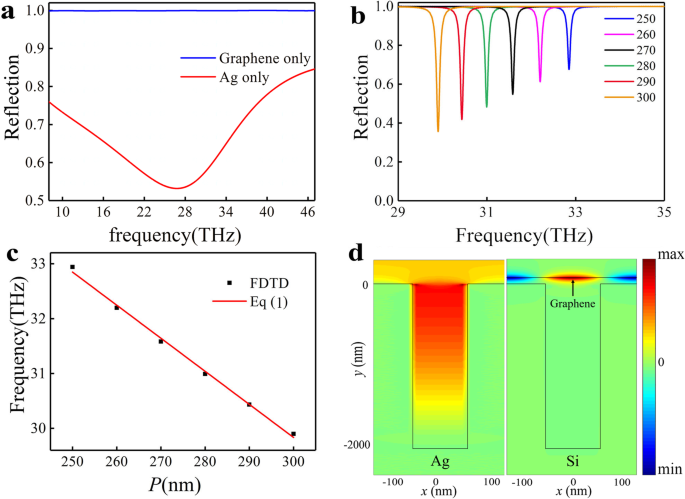
シングルモードの光学応答。 a 法線入射における銀溝のみ（赤い線）とグラフェンのみ（青い線）の構造の反射スペクトル。 b 異なる周期のグラフェン-Si溝の構造の反射スペクトル P ユニットセルの。 c 共振周波数 f の数値モデリングと分析結果 、 それぞれ。 d 電界 E _x F-Pモード（左）とグラフェン準誘導共鳴モード（右）の分布。

ここで k _x = k ₀ sin θ 、 k ₀ =2 π / λ は自由空間の波数ベクトルθです。 は入射光と y の間の角度です -方向、 n _eff はグラフェンのTM導波モードの実効屈折率であり、 G _x は格子の逆格子ベクトルです（ G _x =2 π / P ）。以下の説明では、 y の入射光角度 -方向はゼロです（θ =0°）。他の入射角の状況については、追加ファイル1で説明しています。これらの反射率ディップの位置は、図2bに示すように、グラフェンの準ガイドモードの共振周波数に対応します。シミュレーション結果は、式（1）とよく一致しています。 （1）、ここで m =1であり、有効屈折率〜33は、図2cに示すように、FDTDソリューションによって得られます。電界 E _x F-Pモードとグラフェン準ガイドモードの分布を図2dに示します。 Si溝付き表面によって維持されるSSPモードのエネルギー閉じ込めは、グラフェン準ガイドモードと比較して無視できることに注意してください。

結合状態では、2つの固有モードが互いに近づくと強く結合するため、反射スペクトルが劇的に変化します。図3aに示すように、より広い反射率の低下に加えて、吸光度が約99.97％に向上した狭いサブライン幅の低下が観察されます。垂直距離を増やす場合 g 、反射率ディップの変調が小さくなると、近接場結合と準誘導モードが弱くなります。反射率の低下を小さくする原因として考えられる2つの方法があります。それは、結合度が弱いことと、準ガイドモード励起が弱いことです。したがって、PIAシステムを定量的に理解するために結合発振器モデルを使用しました[38]。

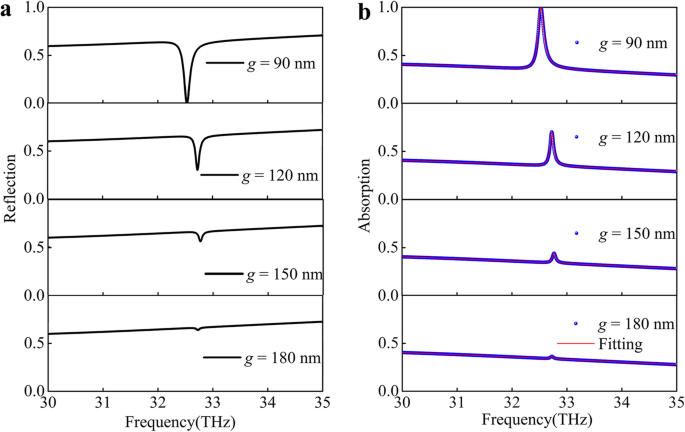
光学応答は、結合距離によって異なります。 a 反射。 b 異なる距離 g の法線入射におけるグラフェン-銀溝の構造の吸収スペクトル グラフェンと銀の溝の間。黒い曲線/青いボールはFDTD法で計算され、赤い曲線は式（1）で分析的に適合されます。 （3）PIAデバイスの

ここで、\（{\ tilde {a}} _ {1,2} ={a} _ {1,2} \ left（\ omega \ right）{\ mathrm {e}} ^ {i \ omega t} \） 、ω _1,2 およびγ _1,2 は、それぞれ明るいモードと暗いモードの時間高調波振幅、共振周波数、および減衰定数です。 b は、明るいモードが入射電界とどの程度強く結合するかを測定する結合係数です。 \（\ tilde {\ kappa} =\ kappa {e} ^ {i \ varphi} \）は、位相遅延効果を表現するために導入された複雑な結合パラメータです。 φ は位相シフトであり、2つのコヒーレント経路間の干渉の形態を決定するための重要な係数です。 φの場合 =0は実際のパラメーターであり、PIT効果の典型的な動作を観察でき、2つのコヒーレント経路間の干渉は破壊的です。 φの場合 =π/ 2は純粋な虚数パラメータであり、2つのコヒーレント経路間の干渉は破壊的から建設的に変換されます[26]。システムの吸収は、式（2）に基づいて散逸エネルギーとして計算できます。これは

次に、数値吸収スペクトルを式（1）でフィッティングします。 （3）異なる g 、図3b（赤い曲線）に示されています。シミュレーション結果は、結合発振器モデルに基づく解析モデリング結果とよく一致しており、PIAデバイスの設計原理を強く確認しています。フィッティングパラメータκ 、φ 、γ ₁ 、およびγ ₂ 図4a–cに示されています。増加する g 結合パラメータκが減少します 、図4aに示すように。カップリングを徐々に減少させる場合（ g を増加させる場合） ）、フェーズφ 変更されておらず、γ ₂ γの間、徐々に減少します ₁ 図4b、cにわずかに示されている変化。結合パラメータκ ダークモードの減衰定数を超えるγ ₂ 最小ギャップ距離の場合、これは、明るいモードから暗いモードへの結合が、グラフェンシートの散逸プロセスよりも強いことを確認します。

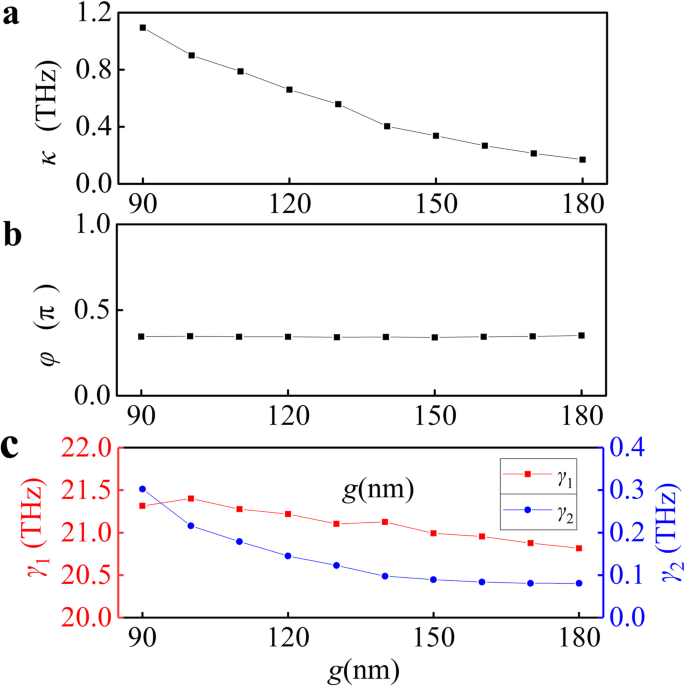
結合システムにおける光学応答の定量分析。抽出された数値（ a ）結合、（ b ）フェーズ、および（ c ）ギャップの関数としての減衰係数 g 。 κの値 、φ 、およびγ ₁ 、γ ₂ 数値吸収スペクトルをフィッティングすることによって抽出されました

明るいモードと暗いモードの間の建設的な干渉を視覚化するために、時間と2つの H による構造の磁場の変化を調査しました。 _z モニターは、グラフェンの中心から3 nm離れて、銀の溝の底から1000nm離れてそれぞれ配置されています。図5aに示すように、2つのモード間の振動位相差は0.5πです。異なる時間での磁場分布は、PIA共鳴周波数 f で計算されました。 _q =32.5 THz、ここでω _q t ₁ 〜2.00πおよびω _q t ₂ 図5b、cに示すように、約2.50π。銀の溝の磁場の最大値は2.00πで観察できますが、グラフェンの磁場は2.50πで最大に達し、2つの構造間の位相がずれていることを示しています。したがって、共鳴の進化と形成は建設的な干渉によって決定されます[39]。

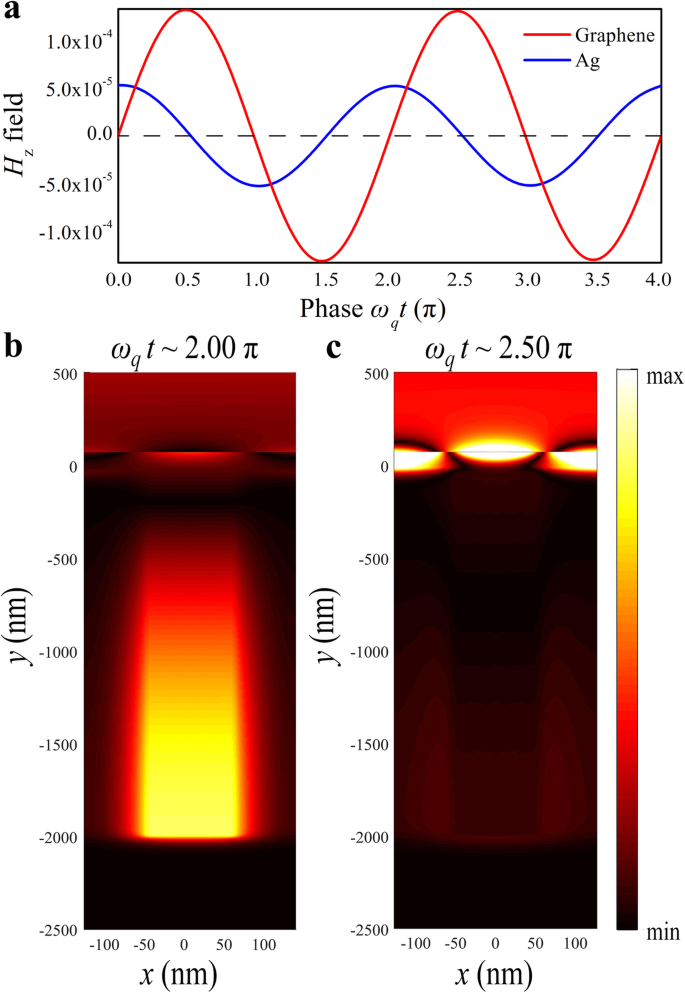
結合モードの時間領域の進化。 a グラフェン（赤い線）と銀の溝（青い線）での磁場強度の計算された時間発展。計算された z g の磁場分布の成分 =90nm。銀溝とグラフェンでの最大電界強度は、異なる時間に観察されます b ω _q t ₁ 〜2.00πおよび c ω _q t ₂ それぞれ〜2.50π

実際のアプリケーションでは、狭い反射帯域と高い消光比が強く望まれます。これらの2つの条件を達成するために、ユニット P の期間を調整できます。 銀溝の深さ d 構造パラメータを最適化するため。さまざまな構造パラメータの反射スペクトルを計算した後 P 1900〜2100nmおよび d FDTDによる245から265nmまで、 P で非常に高い消光比〜99.999％を獲得します。 =254nmおよび d =1980nm。異なる屈折率環境下でのPIAデバイスの反射スペクトルを図6aに示します。センシング機能は[39]：

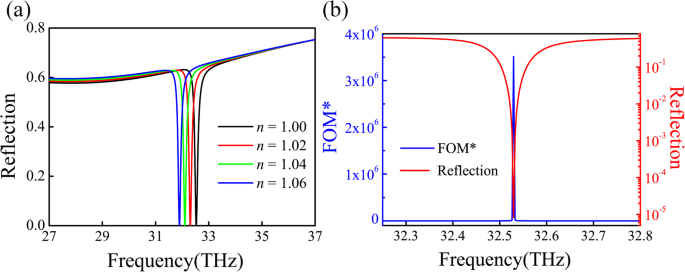
システムのセンシング性能。 a さまざまな誘電環境に対するPIAセンサーの検知応答。 b 関連するFOM *曲線と反射スペクトル

ここで f および私 それぞれ、共振周波数とスペクトル強度です。センサーの反射強度を測定する場合、センサーの感度能力はFOM *値によって定量化できます。値が大きいほど、センサーの感度が高くなります。図6aから、 S を取得できます。 =11.2 THz / RIUおよび関連するFOM〜94.1、半値全幅（FWHM）〜30 nm（0.12 THz）。このFOMは、表面格子共鳴に基づくメタマテリアル吸収体の値よりも大きくなります。また、当社のPIAセンサーは、3.5×10 ⁶ という超高FOM *値をもたらす可能性があります。 、図6bに示すように。最近調査したセンサーのパフォーマンスを追加ファイル1：表S1で比較しました。

PIAシステムでは、グラフェンがもう1つの重要な役割を果たします。共振周波数の変調は、ゲート電圧を調整してグラフェンのフェルミ準位を調整することで実現できます。シミュレートされたスペクトルは、追加ファイル2：図S1および3：図S2に示されています。 PIA共振の周波数シフトアクティブ制御は、センサーまたはアブソーバーにとって意味があります。

結論

要約すると、F-P共鳴モードとグラフェンプラズモン準誘導モードの間の建設的干渉によって誘発される完全な吸収を数値的に示しました。グラフェンプラズモニック準ガイドモードの導入により、銀溝F-P共鳴モードの線幅が狭いスペクトル線が得られます。距離 g のとき 徐々に増加すると、共振強度と線幅が減少します。アプリケーションの場合、システムのFOM *は10 ⁶ を達成できます。 。さらに、吸収ウィンドウは、幾何学的パラメーターとグラフェンフェルミ準位を変えることによって調整できます。これらの結果は、ナノスケールの中赤外線動的スペクトル制御と超高感度光学センサーの実現に向けた新しい方法を提供する可能性があります。

データと資料の可用性

この調査中に生成または分析されたすべてのデータは、この公開された記事[およびその補足情報ファイル]に含まれています。

略語

FDTD：

有限差分時間領域

FOM *：

性能指数*

F-P：

ファブリペロー

FWHM：

半値全幅

PIA：

プラズモンによる吸収

PIT：

プラズモンによる透明性

Q 要因：

品質係数

SSP：

スプーフィング表面プラズモン

TM：

横磁気