オンチップグラフェンベースの非対称ナノキャビティ結合導波路システムにおける動的に調整可能なプラズモン誘起透明度

背景

プラズモン誘起透明度（PIT）は、電磁誘導透明度（EIT）効果に類似した新しい現象であり、広い吸収スペクトル内でシャープな透明度ウィンドウを生成します[1]。スローライト[2、3]、光スイッチング[4]、蓄光[5]、高感度センシング[6、7]などの分野。 PITベースのデバイスは、局所場の増強能力が大きく、表面プラズモンポラリトン（SPP）によって提供される光の古典的な回折限界を克服するため、超コンパクトなフットプリントで実現できます[8、9]。結合共振器システム[10、11、12、13]、フォトニック結晶構造[14、15]、メタマテリアル構造[16、17]など、プラズモニックナノ構造でPIT効果を実現するためにさまざまな設計が提案されています。ただし、PIT効果を示すこれらの構造のほとんどは、構造の幾何学的パラメータを変更しない限り、ほとんど調整できません。これにより、PITウィンドウのアクティブな制御が大幅に制限され、品質が低下します。

二次元（2D）ハニカム格子に配置された炭素原子の単分子層であるグラフェン[18]は、極限閉じ込めの能力を含むその並外れた電気的および光学的特性により、高効率のオプトエレクトロニクスデバイスを開発する大きな可能性を示しています[19,20、 21]、動的調整可能性、および比較的低い減衰損失[22、23]。特に、グラフェンの表面伝導率は、外部ゲート電圧または化学ドーピングを介して化学ポテンシャルによって動的に調整できます[24、25]。これにより、グラフェンは、幾何学的パラメーターを固定しながら、調整可能なPITを設計するための有望な候補になります。従来の貴金属と比較してこれらの並外れた特徴のために、グラフェンリング共振器結合グラフェン導波路のPIT現象[26、27]やグラフェン効果のPIT効果など、グラフェンベースのPITを実現するために幅広い研究が行われてきました。グラフェン長方形共振器構造と結合したグラフェンベースのナノリボン導波路[28、29]。 Sun etal。マルチスペクトルPIT応答が達成されたテラヘルツ周波数範囲で誘電体層によって分離された周期的にパターン化されたグラフェン二重層構造を研究しました[30]。さらに、調整可能なPIT効果は、周期的に組み合わされたグラフェンナノストリップで実現され、結合されたローレンツ振動子モデルで分析的に記述されます[31、32]。ただし、これまでの研究のほとんどは、単層グラフェンまたはグラフェンナノリボン導波路システムに結合されたグラフェン共振器、および通常の入射光を伴うグラフェンナノストリップシステムに関するものでした。局所的に変化する化学ポテンシャルを持つグラフェンシートでプラズモン的に誘発された透明現象についての研究はほとんど、あるいはまったくありませんでした。さらに、通常の入射光と比較して、面内伝搬には、オンチップ統合に圧倒的な利点があります。

上記の基礎研究を動機として、本論文では、同じグラフェン単分子層上のU字型ナノキャビティと長方形ナノキャビティにサイドカップリングされたプラズモニックバス導波路で構成されるグラフェンベースのプラズモニックナノ構造を提案します。有限要素法（FEM）に基づく商用ソフトウェアCOMSOL Multiphysicsを使用して、設計の伝達および電磁応答を調査します。シミュレーション結果は、PIT現象が提案されたプラズモンナノ構造で観察されることを明らかにしています。さらに、PITウィンドウは、ナノキャビティとプラズモンバス導波路の化学ポテンシャルを変化させることによって効果的に調整できます。また、結合モード理論（CMT）を導入して、PIT現象の伝達特性を説明します。最後に、提案されたプラズモンナノ構造に基づくプラズモン屈折率センサーが研究されている。 333.3 nm /屈折率ユニット（RIU）の検出感度は、PIT透過ピークで達成されます。また、群遅延が1psを超えるスローライト効果が実現されます。この提案された新しいプラズモンナノ構造は、グラフェン単層上にグラフェンベースのオンチップ高密度プラズモンデバイス統合を実現するための新しい方法を提供する可能性があります。

メソッド

簡単にするために、提案された構造は、対応するバス導波路とナノ共振器を形成するために化学ポテンシャルの局所的な変化を伴う浮遊グラフェン単分子層によってモデル化されます。図1aは、プラズモンバス導波路に直接結合されたU字型ナノキャビティの概略構成と幾何学的パラメータを示しています。化学ポテンシャルがμのU字型ナノキャビティ結合導波路 _c2 化学ポテンシャルがμの同じグラフェンシートに囲まれています _c1 。プラズモンバス導波路の幅dは20nmです。 U字型のナノキャビティの幅と高さは W です。 _U =150nmおよび L _U =それぞれ120nm。このような構造の正確な理論的モデリングには、3次元（3D）計算が必要であり、これには非常に時間とメモリがかかります。この問題を解決するために、実効屈折率法が多くの出版物で使用されており[33、34、35]、構造の屈折率は、伝搬定数間の比率によって定義されるガイドモードの実効屈折率に置き換えられています。と自由空間の波数。私たちの構造では、グラフェンシートは n として定義される実効屈折率によって特徴付けられる超薄膜として扱われます _eff =β / k ₀ 、ここで k ₀ =2 π / λ は自由空間の波数です。伝播定数β 単層グラフェンによってサポートされるガイド付きSPPモードの例は、[36、37]

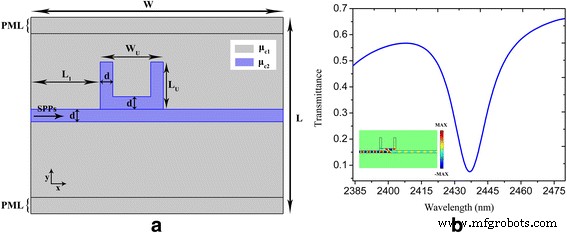
a、b U字型ナノキャビティ結合導波路システムの概略構成と幾何学的パラメータ、および対応するスペクトル透過率。 挿入図 b で 電界を示します（ E _y ）2437nmの波長での分布。パラメータは W として設定されます =800 nm、 L =620 nm、 d =20 nm、 W _U =150 nm、 L _U =120 nm、 L ₁ =220 nm、τ =1 ps、μ _c1 =0.3eV、およびμ _c2 =0.9eV。完全一致レイヤー（ PML ）幅50nmの top が実装されています および下 ドメイン境界からの望ましくない反射を排除するための計算ドメインの

ここでμ ₀ およびε ₀ それぞれ真空の透磁率と誘電率を表し、μ _r およびε _r それぞれ、比透磁率と比誘電率を表します。グラフェンの表面抵抗率σ _g バンド間電子遷移で構成されるσ _inter バンド内電子-光子散乱σ _イントラ 久保公式[38、39]

あり

ここでμ _c はグラフェンの化学ポテンシャル、ω プラズモンの角周波数、ћ 縮小プランク定数 e は電子の電荷、 k _B ボルツマン定数 T は温度、ℏ=h / 2 π は縮小プランク定数であり、τ 電子の運動量緩和時間です。具体的には、グラフェンの化学ポテンシャルは、化学ドーピングまたは電気的ゲーティングを介して調整できます[25、26]。 Mikhailov etal。グラフェンシートのキャリア密度が10 ¹⁴ であることを実験的に示しています。 cm ⁻² 達成されたため、250 K未満の温度で1〜2eVの化学ポテンシャルが得られました[40]。さらに、10 ⁵ の直流移動度を備えた高品質の懸濁グラフェンが実証されています。 cm ² V ^-1 s ^-1 τに対応するが得られます> 1.5ps [41]。この論文では、私たちが設定した緩和時間と化学ポテンシャルの両方が、数値研究の信頼性を確保するのに十分に保守的です。

結果と考察

SPP波が図1aに示す側面結合されたU字型ナノキャビティを通過すると、エネルギーがナノキャビティに結合されます。入射波とナノキャビティからの脱出電力との間の破壊的な干渉により、共鳴波長で深い透過谷が得られます[12、13]。図1bは、τでプラズモンバス導波路に直接結合されたU字型ナノキャビティの透過スペクトルをプロットしたものです。 =1 ps、μ _c1 =0.3eV、およびμ _c2 =0.9eV。透過率が0.1未満の顕著なディップは、2437nmの共振波長で達成されます。図1bの挿入図は、共鳴波長での対応する電界分布を示しています。ここでは、プラズモン導波路を介して伝播するSPPはほとんどないことがわかります。図2aは、緩和時間τを変化させた場合の透過率スペクトルを示しています。 =0.6、0.8、および1 ps。ここで、緩和時間が長くなると、より高い透過コントラストが達成されることがわかります。これは、電子運動量の緩和時間が増加すると、プラズモンのオーム吸収が減少するためです[39]。さまざまな化学ポテンシャルμに対するU字型ナノキャビティ結合導波路システムの計算された透過率 _c2 図2bに示されています。緩和時間τ および化学ポテンシャルμ _c1 それぞれ1psと0.3eVとして常に維持されます。ディップの位置は、ナノキャビティとバス導波路のさまざまな化学ポテンシャルを介して動的に調整されていることがわかります。ディップの中心波長は2455、2445、および2437 nmで、μです。 _c2 =それぞれ0.89、0.895、0.9eV。

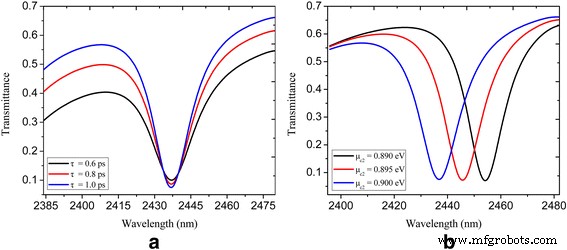
図1に示すU字型ナノキャビティ結合導波路システムのスペクトル透過率： a τで =0.6、0.8、および1 ps; μ _c1 =0.3eV;およびμ _c2 =0.9eV; b μで _c2 =0.89、0.895、および0.9 eV; μ _c1 =0.3eV;およびτ =1ps

CMT [12、42、43]によると、周波数ωの共振モードをサポートするシステムのスペクトル透過率 ₀

ここで、1 / τ _i および1 / τ _e ナノキャビティ内の固有損失の減衰率と、プラズモンバス導波路を介して逃げる電力をそれぞれ表します。明らかに、最小透過率 T _min =（1 / τ _i ） ² /（1 / τ _i + 1 / τ _e ） ² 入射光の周波数がωの場合に達成できます 共振周波数ωに等しい ₀ 。 1 / τとして _e 1 / τをはるかに超えています _i 、ほぼゼロの透過ディップが得られ、シミュレーション結果とよく一致しています。

PIT効果を得るために、図1に示すプラズモンナノ構造に基づく長方形ナノキャビティを追加します。U字型および長方形のナノキャビティにサイドカップリングされたプラズモンバス導波路で構成されるグラフェンベースのプラズモンナノ構造を図1に模式的に示します。 。3a。プラズモンバス導波路を介して接続されている場合、2つのナノキャビティ間に強い結合が存在します。 U字型と長方形のナノキャビティに関連する2つの共鳴励起経路間の破壊的な干渉により、PIT現象が発生します[10、11]。図3bに示すように、鋭い透過ピーク（0.06から0.44に増加）が図1bに示す透過禁止バンドに現れ、PITウィンドウの形成を示しています。 PITウィンドウの中心波長は2437nmであり、これは図1bに示す透過ディップの中心波長の位置とまったく同じです。 U字型ナノキャビティの広い共鳴は2つの共鳴モードに分割されます。1つは青方偏移され、もう1つは赤方偏移されます[12、13]。図3c–eは、それぞれ2408、2437、および2457nmでの共振モードの電界分布を示しています。ナノキャビティ内の電界分布は、2437 nmでのプラズモニックバス導波路内の電界分布と同相であることがわかります。これは、入射光とナノキャビティからプラズモニックバス導波路に逃げる光がコヒーレントな増強に遭遇することを意味します。 。さらに、電界分布は、2408および2457 nmでナノキャビティとプラズモンバス導波路の間に逆位相があることを示しています。つまり、破壊共鳴の条件が満たされ、透過波が抑制されています[12]。

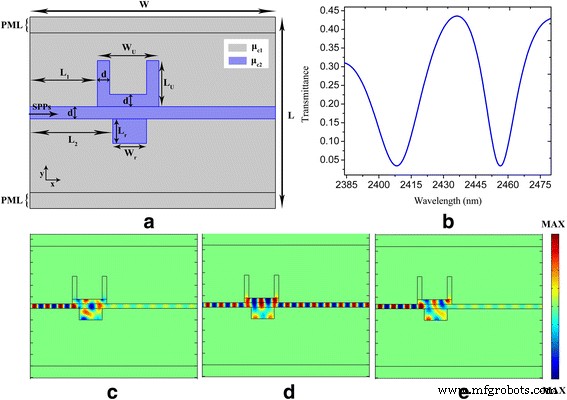
a、b U字型および長方形のナノキャビティ結合導波路システムの概略構成と幾何学的パラメータ、および対応するスペクトル透過率。 c – e 電界（ E _y ）それぞれ2408、2437、および2457nmの波長での分布。パラメータは W として設定されます =800 nm、 L =620 nm、 d =20 nm、 W _U =150 nm、 L _U =120 nm、 L ₁ =220 nm、 L ₂ =250 nm、 L _r =50 nm、 W _r =100 nm、τ =1 ps、μ _c1 =0.3eV、およびμ _c2 =0.9eV

緩和時間τを変化させたU字型および長方形のナノキャビティ結合プラズモンバス導波路システムのスペクトル透過率を計算します。 =0.6、0.8、および1 psであり、結果を図4aに示します。緩和時間の増加とともに透過コントラストが増加することがわかります。さらに、PITウィンドウの動的調整可能性を図4bに示します。化学ポテンシャルμ _c1 μの間、常に0.3eVに保たれます _c2 は0.89、0.895、および0.9eVです。化学ポテンシャルとしてμ _c2 が増加すると、PITウィンドウの透過ピーク（波長2452、2445、および2437 nm）が明らかにブルーシフトします。その結果、動的に調整可能なPIT効果は、ナノキャビティとプラズモンバス導波路の化学ポテンシャルを変更することにより、提案されたナノ構造で実現されます。

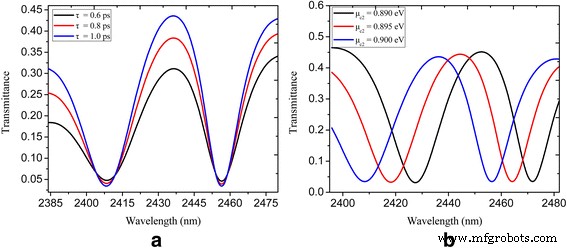
図3に示すU字型および長方形のナノキャビティ結合導波路システムのスペクトル透過率： a τで =0.6、0.8、および1 ps; b μで _c2 =0.89、0.895、および0.9 eV

幾何学的パラメータがPIT現象にどのように影響するかを調査するために、長方形のナノキャビティの位置を変更しました。図5aは、U字型および長方形のナノキャビティ結合プラズモンバス導波路システムのスペクトル透過率を示しています。ここでは、透過率のピークが高くなり（0.44から0.52に増加）、PITウィンドウが L <で広くなっていることがわかります。 / i> ₂ 2つのナノキャビティ間の結合強度の強化に起因する特定の範囲で増加します[11、28]。また、図5bに示すように、長方形のナノキャビティの幅を狭くすると、透過ピークが高くなる（0.44から0.48に増加）可能性があることがわかります。これは、PITウィンドウを調整するための別のオプションを提供します。 PITウィンドウの品質係数（Q係数）はλとして定義されます。 ₀ / ∆ λ 、ここでλ ₀ および∆ λ 透過ピーク波長と半値全幅（FWHM）です。提案されたプラズモンナノ構造では、30 nm未満のFWHMと約80のQファクターが得られます。これは、前述の参考文献[28、29]で提案されたグラフェンベースのPITの対応物よりもはるかに狭くて高いです。

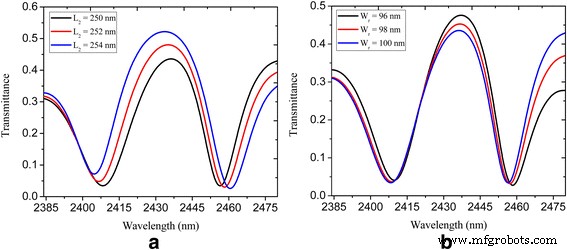
図3に示すU字型および長方形のナノキャビティ結合導波路システムのスペクトル透過率： a L で ₂ =250、252、および254 nm; b W で _r =96、98、および100 nm

CMTに従って、プラズモンナノ構造の透過率は[12、42]

として表されます。 $$ T ={\ left | \ frac {j \ left（{\ omega} _ {\ mathrm {U}}-{\ omega} _ {\ mathrm {r}} \ right）+ \ gamma +1} { j \ left（{\ omega} _ {\ mathrm {U}}-{\ omega} _ {\ mathrm {r}} \ right）+ \ beta + \ gamma +1} \ right |} ^ 2 $$（ 6）

ここで、γ およびβ 2つのナノキャビティ間の結合係数、およびナノキャビティとプラズモンバス導波路間の結合係数をそれぞれ表します。 U字型ナノキャビティの共振周波数ωの場合にPITウィンドウが得られることがわかります。 _U 長方形のナノキャビティω _r ほぼ同等です。そして、対応する透過ピークは|（γ + 1）/（β + γ + 1）| ² 。

図3aに示す構造に基づいて、屈折率センサーを構築します。これは、式（1）の比誘電率を変更することによって実現されます。 1.図6aは、屈折率が異なる場合のスペクトル透過率を示しています n 、これは、アンダーセンシング材料の屈折率を指します。屈折率 n の場合、ピーク/ dip1 / dip2波長が2437.3から2457.3nm /2410.3から2432.4nm /2457.3から2474.9nmにシフトすることがわかります。 1から1.06まで変化します。屈折率として n 増加すると、透過ピークとディップの両方が赤方偏移を示します。屈折率センサーの検出感度。屈折率の単位変動あたりのピーク/ dip1 / dip2波長のシフトとして定義されますdλ/ dn それぞれ333.3、368.3、および293.3 nm / RIUです。図6bは、屈折率 n でのスペクトル透過率のピークとディップを示しています。 1から1.19まで変化します。ここで、ピーク/ディップ波長と屈折率のほぼ線形の関係を見ることができます n 。

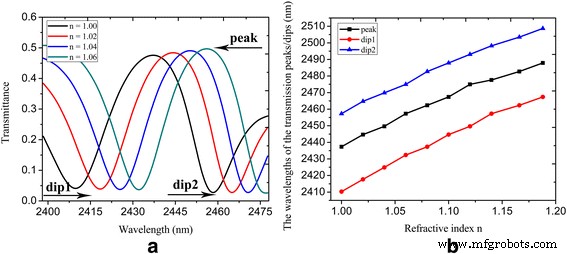
a 屈折率 n のスペクトル透過率 =1、1.02、1.04、および1.06; b スペクトル透過率のピーク/ディップ波長と屈折率 n 。パラメータは W として設定されます =800 nm、 L =620 nm、 d =20 nm、 W _U =150 nm、 L _U =120 nm、 L ₁ =220 nm、 L ₂ =250 nm、 L _r =50 nm、 W _r =96 nm、τ =1 ps、μ _c1 =0.3eV、およびμ _c2 =0.9eV

PIT現象は、急激な分散によって引き起こされる遅い光の影響を伴うことはよく知られています[13、29]。スローライト効果は、τとして表される群遅延によって特徴付けることができます。 _g =∂φ （ω ）/∂ω ここで、φ （ω ）は、透過スペクトルの有効な位相シフトです。図7では、さまざまな化学ポテンシャルμでのPITウィンドウ内のグループ遅延をプロットしています。 _c2 。 PIT透過ピークの近くでは、遅い光の影響を示す大きな正のグループ遅延を提供します。 μでのPITシステムのピーク波長 _c2 =0.89、0.895、および0.9 eVは、それぞれ2449.7、2442.3、および2434.7 nmであり、対応するグループ遅延は、それぞれ0.99、1.1、および1.02psです。したがって、スローライト効果は、ナノキャビティとプラズモンバス導波路の化学ポテンシャルを変更することによって効果的に調整されます。これは概念実証の記事であることも指摘しておく必要があります。実際には、提案された構造は、屈折率が空気よりも大きい基板上にある必要があり、それに応じて周波数応答がシフトします。また、損失の増加を伴うプラズモンの閉じ込めが高くなり、その結果、透過スペクトルの透明ウィンドウのピーク値が減少します。ただし、原則は一時停止の場合と同じです。

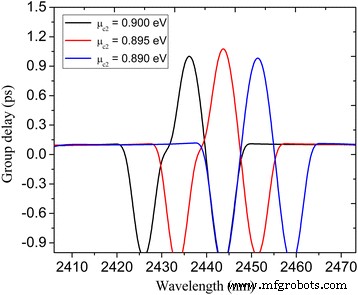
グループ遅延対化学ポテンシャルμ _c2 図3aに示すグラフェンPITシステムの場合。その他のパラメータは W として設定されます =800 nm、 L =620 nm、 d =20 nm、 W _U =150 nm、 L _U =120 nm、 L ₁ =220 nm、 L ₂ =254 nm、 L _r =50 nm、 W _r =96 nm、τ =1 ps、μ _c1 =0.3eV