単結晶6H-SiCのすべり変形とナノメートル加工性の原子スケールの特性化

はじめに

SiCは、バンドギャップの広い第3世代の半導体材料として、高い破壊電界、高い耐放射線性、高速のキャリア飽和、速い熱伝導率、小さな誘電率、安定した化学特性を備えているため、幅広い分野での用途があります。高温、高周​​波、高出力、耐放射線、短波長の光電子デバイスと光電子統合の組み合わせ[1]。

SiCの最も広く使用されている結晶は、3C、4H、および6Hです。単結晶SiCの機械加工では、研削/ラッピング/研磨などの加工方法が依然として主な方法です。ただし、ダイヤモンドとSiCの硬度比は2：1（加工深さ<50 nm）に近く、機械加工の推奨値である5：1よりもはるかに低くなっています[2]。切削工具の激しい摩耗と表面下の損傷は、ウェーハの品質に直接影響します。これらの問題に対処するために、ナノスケールでのSiCの除去挙動を理解するために多くの研究が行われてきました。 3C-SiCの除去メカニズムと、切削プロセス中の塑性変形メカニズム[3,4,5,6,7]、工具摩耗[8]、摩擦挙動[9]などの加工係数の影響が徹底的に研究されています。 ]、および3C-SiCの異方性[10]および切削温度の影響[11]。

6H-SiCはより複雑なABCACBスタック構造を持っています。 SPDT（シングルポイントダイヤモンド旋削）処理における6H-SiCの除去メカニズム（材料除去プロセス[12]および脆性-延性遷移[13]に対する工具すくい角の影響など）が研究されていますが、研究は明らかに3C-SiC未満。 6H-SiC（3 eV）のバンドギャップは、3C-SiC（2.3 eV）のバンドギャップよりも明らかに高くなっています。現在、6H-SiCロッド成長プロセスの技術レベルは3C-SiCよりもはるかに高いです。 6H-SiCは、3C-SiCよりもはるかに多くの産業用途で使用されています。対応するデバイスは、ショットキー整流器、サイラトロン、パワーMOSFET（金属-酸化物-半導体電界効果トランジスタ）など、高周波、高電力、および高温のフィールドに適用されています。 6H-SiCの加工面/表面下品質を向上させるために、現時点で最も効率的かつ効果的な手段は、6Hのプロセスにより適した結晶面（加工面）/結晶方位（加工方向）の適切な組み合わせを見つけることです。 -SiC。

スクラッチ実験とシミュレーションは、除去動作を調査するための最も一般的で効果的な方法のいくつかです[14、15]。引っかきプロセス中の材料除去メカニズムの研究は、実際の研磨加工プロセスにとって大きな指針となる重要性を持っています。分子動力学法は、ナノスケールで損傷の形成と除去のプロセスを提供することができます。したがって、分子動力学スクラッチシミュレーションを使用して、結晶学によって誘発された異方性の影響下での6H-SiCの除去挙動を分析しました。

方法論

この論文の切削シミュレーションは、大規模な原子/分子の大規模並列シミュレータ（LAMMPS）を使用して完了しました[16]。この研究では、モデルの可視化と欠陥の識別にOIVTO [17]とダイヤモンド構造の識別方法[18]を使用しました。ワークピースとツールのモデリングの実装は、他のソフトウェアを使用せずにLAMMPSに依存していました。図1a–cに示すように、ワークピースとツールの両方を変形可能なボディとして設定し、シミュレーション中に摩耗挙動を調査しました。ツールとワークピースのモデルは、境界原子層、サーモスタット原子層、およびニュートン原子ゾーンの3つの部分に分割されました。ワークピースを初期位置に保つために、ワークピースの下端と右端の境界層原子を固定しました。サーモスタット層とニュートン層の原子は、ニュートンの第2法則に従います。 y に沿って周期境界が適用されました 方向。スクラッチシミュレーションの前に、モデルはベレンゼンサーモスタット法を使用したNVEアンサンブルによって緩和されました。定常エネルギー状態を得るために、スクラッチシミュレーションの前に50psの緩和期間が適用されました。研磨形状は、端から端までの角度が90°の球形のクラウン三角錐です。図2に示すように、6H-SiCの共通結晶面（a面（基底面）、m面（プリズム面）、c面）を加工面として選択しました。構造の対称性を考慮して、次の平面/方向の組み合わせが加工面/加工方向として選択されました：\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、 \（（0001）/ \ left [10 \ overline {1} 0 \ right] \）、\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline { 1} 0 \ right] \）、\（\ left（01 \ overline {1} 0 \ right）/ \ left [0001 \ right] \）、\（\ left（11 \ overline {2} 0 \ right） / \ left [1 \ overline {1} 00 \ right] \）、および\（\ left（11 \ overline {2} 0 \ right）/ \ left [0001 \ right] \）。シミュレーションの処理パラメータを表1に示します。引っかきシミュレーションの前に、研磨剤をワークピースの左側に配置し、研磨剤の先端はワークピースの上面から50Å下にあります。研磨剤とワークピースの間の最も近い距離は30Åであり、相互作用電位のカットオフ範囲から遠く離れています。研磨剤は、ワークピースの自由端から x の正の方向に移動します。 -軸を作成し、スクラッチプロセスを完了します。

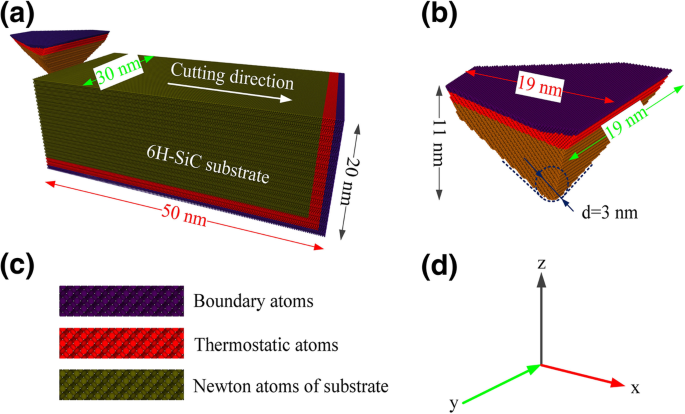
a ナノスクラッチシミュレーションのMDモデル。 b ツールの形態。 c モデルの構造。 d 軸方向

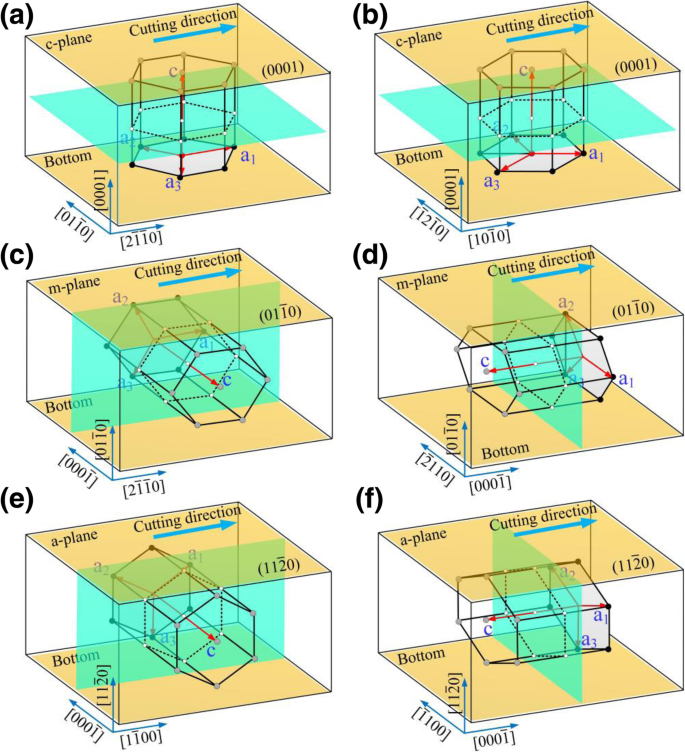
スクラッチプロセスの概略図。 a – f 対応するプロセスモードは\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（（0001）/ \ left [10 \ overline {1} 0 \ right ] \）、\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（\ left（01 \ overline { 1} 0 \ right）/ \ left [0001 \ right] \）、\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）、および\（\ left（11 \ overline {2} 0 \ right）/ \ left [0001 \ right] \）、それぞれ

原子ポテンシャル関数は、分子動力学シミュレーションの精度と信頼性において重要な役割を果たします。単結晶SiCの機械的特性と除去メカニズムに関する以前のテストとシミュレーションによると、Erhart and Albe [19]によって提案された分析結合次数ポテンシャル（ABOP）関数は、シリコンと炭素の相互作用により適しています。ポテンシャル関数で使用されるパラメーターを表2に示します[19]。 Tersoffポテンシャルエネルギー関数[6]の代わりに、ABOPポテンシャル関数を使用して、処理中のツールとワークピース内およびツールとワークピース間のSi-Si、CC、およびSi-C相互作用を定義します[2、7、8、10。 11]。

結果と考察

ナノメトリックマシナビリティ分析

図1と図2に示すように。図3および4に示すように、6H-SiCの異方性は、ナノメートルの機械加工性（加工深さ、除去モード、除去量、および表面下損傷深さ（SSD）など）に大きな影響を及ぼしました。加工面/加工方向と基底面/ c の関係による -軸（図3を参照）では、材料処理モードは3つのカテゴリに分類できます。（i）底面が加工面として選択され、（ii）底面が加工面に垂直であり、 c -軸は加工方向に垂直であり、（iii） c -軸は加工方向に平行です。

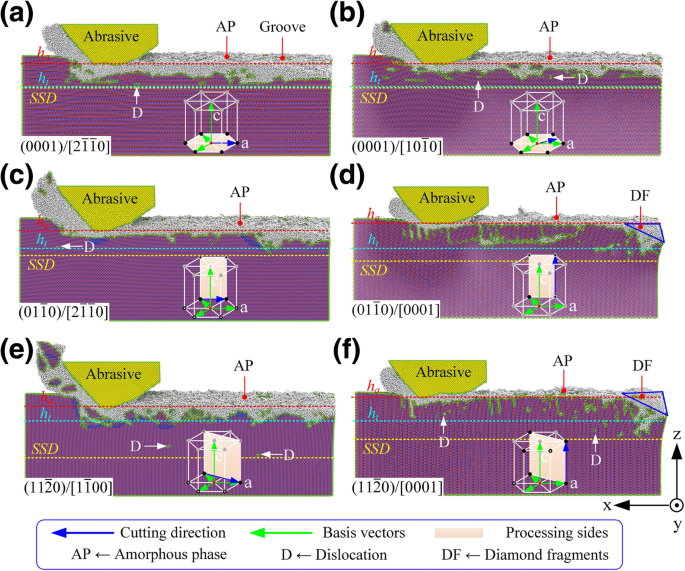
さまざまな結晶面/配向条件下での機械加工された表面のトポグラフィー。ここで、 a – f 対応するプロセスモードは\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（（0001）/ \ left [10 \ overline {1} 0 \ right ] \）、\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（\ left（01 \ overline { 1} 0 \ right）/ \ left [0001 \ right] \）、\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）、および\（\ left（11 \ overline {2} 0 \ right）/ \ left [0001 \ right] \）、それぞれ

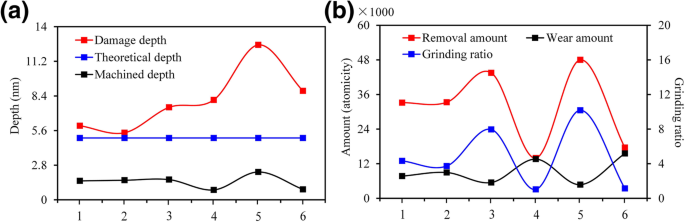
さまざまな結晶面/配向条件下でのナノメートルの機械加工性、 a 加工深さと損傷深さに対する異方性の影響、 b 除去量、摩耗量、粉砕率に及ぼす異方性の影響。 1、2、3、4、5、および6は、対応するプロセスメソッド\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（（0001）/ \ left [10 \ overline {1} 0 \ right] \）、\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（\ left（01 \ overline {1} 0 \ right）/ \ left [0001 \ right] \）、\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）、および\（\ left（11 \ overline {2} 0 \ right）/ \ left [0001 \ right] \）、それぞれ。損傷層の深さは、引っかき傷によって引き起こされる結晶の内部欠陥の最大深さを指します。理論上の深さは、処理前に事前設定された深さを指します。加工深さは、引っかき傷後の残留深さを指します。除去量とは、ワークの材料が除去される原子の数を指します。摩耗量とは、スクラッチ前後の砥粒の原子数の差を指します

（i）図3a、bに示すように、処理モードを\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0]として選択した場合、6H-SiCのナノメートル加工性は非常に類似していました。 \ right] \）および\（（0001）/ \ left [10 \ overline {1} 0 \ right] \）。ただし、処理モードを\（（0001）/ \ left [10 \ overline {1} 0 \ right] \）として選択した場合、6H-SiCの除去プロセスは脆性モードに傾く傾向がありました。 （ii）図3c、eに示すように、処理モードが\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0として選択された場合\ right] \）と\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）、加工深さと材料除去量はそれらよりも大幅に高かった他の処理方法で。図4に示すように、同じ理論処理深度（ h _t =5.0 nm）、処理モードでの材料除去率\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）は3.4倍でした処理モードの場合\（\ left（01 \ overline {1} 0 \ right）/ \ left [0001 \ right] \）。材料加工率（材料除去量/工具摩耗）は10.1でしたが、この加工パラメータでのSSDも他の加工条件でのSSDよりもはるかに高く、\（（0001）/ \ left [10 \ overline { 1} 0 \ right] \）。機械加工された表面とチップには多数のナノクリスタライトがありました。この状態で多数の脆性破壊が発生しました。処理モード\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）は、高い処理効率を必要とするが、地下の損傷。 \（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）の材料除去率は、\（\ left （11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）しかし、SSDは後者の50％にすぎませんでした。また、加工面のアモルファス層の厚さは、\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）や\（（0001））よりもはるかに薄い。 / \ left [10 \ overline {1} 0 \ right] \）。表面下の相分布は均一であり、溝全体の機械的特性は他の加工方法よりも優れていた。したがって、処理モード\（\ left（01 \ overline {1} 0 \ right）/ \ left [0001 \ right] \）は、6H-SiC表面のマイクロナノ溝を高効率で処理するための最良の選択です。 、高精度、低SSD。 （iii）図1および2に示すように。 3d、f、加工方向が c に平行な場合 -軸、チップは初期処理段階でひどく摩耗していました。加工深さと材料除去率は他の加工方法よりもはるかに低く、材料加工率は約1.0でしたが、SSDの\（\ left（01 \ overline {1} 0 \ right）/ \ left [ 0001 \ right] \）および\（\ left（11 \ overline {2} 0 \ right）/ \ left [0001 \ right] \）処理モードは\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）。したがって、\（\ left（01 \ overline {1} 0 \ right）/ \ left [0001 \ right] \）および\（\ left（11 \ overline {2} 0 \ right）/を使用することはお勧めしません。 \ left [0001 \ right] \）6H-SiCの表面のマイクロナノ溝の処理。ただし、これらのモードは優れた耐摩耗性を示します。そのため、鉄金属の超精密加工の分野で幅広い展望を持つ単結晶SiC切削工具のすくい面に適しています。

唇の動きと表面下の損傷分布の分析

三角錐の先端に基づく引っかきプロセスにおけるシュミットファクターの分布

六方晶系の一般的なすべり系（図4を参照）には、主に基底すべり、角柱すべり、錐体すべりが含まれます。滑り抵抗は、一般化された積層欠陥エネルギー（GSF）とd E に関連しています。 _GSF / d x 対（ x / b ）スリップシステムの。スリップ運動は、最も密度の高い平面で、最も短い方向に沿って発生します[10]。基礎すべりの優先スリップシステムは、基礎すべり（シャッフルセット）/ <\（1 \ overline {1} 00 \）>と基礎すべり（シャッフルセット）/ <\（11 \ overline {2} 0 \）>です。 [20]。前者は中間エネルギー最小値を欠いているため、シミュレーションと実験では後者が優先されます[20]。したがって、この作業で考慮されるすべり運動は次のとおりです。基底すべり（シャッフルセット）/ <\（11 \ overline {2} 0 \）>および角柱状のすべりとすべり。図5。

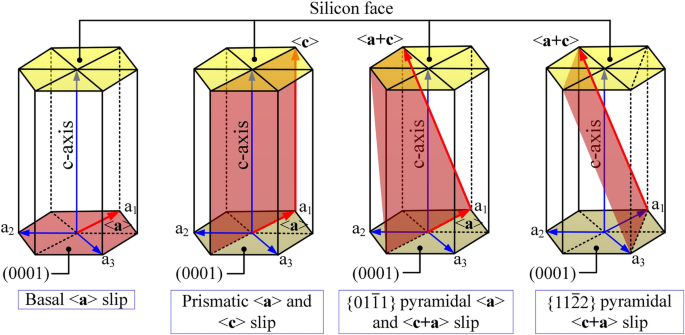
六角形のすべり系

グライドプレーンのせん断応力成分τ _ss 次の関係で計算できます：

$$ {\ tau} _ {\ mathrm {ss}} ={\ sigma} _ {\ mathrm {cont}} \ mathit {\ cos} <\ overset {\ rightharpoonup} {f}、\ overset {\ rightharpoonup} {n_g}> \ cos <\ overset {\ rightharpoonup} {f}、\ overset {\ rightharpoonup} {t_g}> ={\ sigma} _ {\ mathrm {cont}} \ bullet m $$（1）

ここで、σ _続き は接触応力、\（\ overset {\ rightharpoonup} {f} \）は荷重方向、\（\ overset {\ rightharpoonup} {n_g} \）および\（\ overset {\ rightharpoonup} {t_g} \）はグローバルデカルト座標系でのすべり面の法線とすべり方向、および m シュミット係数です。グローバル座標系を固定し、ローカル座標系を結晶の方向に回転させました。 x -ローカル座標系の軸は基本ベクトル\（\ overset {\ rightharpoonup} {a_1} \）に平行でしたが、 z -軸は基本ベクトル\（\ overset {\ rightharpoonup} {c} \）と平行でした。

引っかき加工中、三角錐先端の主接触面はすくい面でしたが、工具がひどく摩耗すると、主接触面はすくい面とチップトップの複合に移行しました。対応する荷重方向\（\ overset {\ rightharpoonup} {f} \）は

として表示されます $$ \ left \ {\ begin {array} {c} \ overset {\ rightharpoonup} {f_1} =\ left（{f} _ {1x}、{f} _ {1y}、{f} _ {1z} \ right）\ kern8em \ mathrm {rake} \ \ mathrm {face} \ \\ {} \ overset {\ rightharpoonup} {f_2} =\ left（{f} _ {2x}、{f} _ {2y}、 {f} _ {2z} \ right）\ kern9.75em \ mathrm {tip} \ \ mathrm {top} \ end {array} \ right。 $$（2）

ここで、\（\ overset {\ rightharpoonup} {f_1} =\ left（1,0、-\ sqrt {2} \ right）\）、\（\ overset {\ rightharpoonup} {f_2} =\ left（0,0 、-1 \ right）\）グローバル座標系で。

六方晶系として、6H-SiCのスリップ系は{ h k i l } / < u v t w >。ローカルデカルト座標系でのすべり平面法線\（\ overset {\ rightharpoonup} {n_c} \）とすべり方向\（\ overset {\ rightharpoonup} {t_c} \）は次のように表示されます

$$ \ overset {\ rightharpoonup} {n_c} =\ left（\ frac {3} {2} h、\ frac {\ sqrt {3}} {2} \ left（h + 2k \ right）、\ frac { 3 la} {2c} \ right）$$（3）$$ \ overset {\ rightharpoonup} {t_c} =\ left（u- \ frac {1} {2} \ left（v + t \ right）、\ frac {\ sqrt {3}} {2} \ left（vt \ right）、\ frac {c} {a} w \ right）$$（4）

グローバルデカルト座標系でのすべり平面法線\（\ overset {\ rightharpoonup} {n_g} \）とすべり方向\（\ overset {\ rightharpoonup} {t_g} \）は次のように表示されます

$$ \ overset {\ rightharpoonup} {n_g} =T \ bullet \ overset {\ rightharpoonup} {n_c} $$（4）$$ \ overset {\ rightharpoonup} {t_g} =T \ overset {\ rightharpoonup} {\箇条書き{t} _c} $$（5）

ここで、グローバル座標系からローカル座標系への回転行列の形式と、対応する回転角を表3に示します。

<図>

式（1）〜（5）によると、荷重方向が\（\ overset {\ rightharpoonup} {f_1} \）および\（\ overset {\ rightharpoonup} {f_2} \の場合の、対応するスリップシステムのシュミット係数）を表4に示します。（i）6H-SiCのc / a値は4.901に達し、1.633よりはるかに大きくなっています。したがって、基礎すべりに必要な臨界せん断応力は、角柱すべりシステムのそれよりも低かった。加工面が基底面の場合、すべり系の係数は他のすべり系よりも高かった。したがって、処理モードが\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）および\（（0001）/ \ left [10 \ overline {1 } 0 \ right] \）、基本的なスリップモーションが最初に発生しました。 （ii）処理モードが\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）および\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）、読み込み方向のみを考慮\（\ overset {\ rightharpoonup} {f_1} \）および\（ \ overset {\ rightharpoonup} {f_2} \）、理論的には基底すべりが発生することは不可能であり、角柱状のすべり運動が優先されました。 （iii）処理モードが\（\ left（01 \ overline {1} 0 \ right）/ \ left [0001 \ right] \）および\（\ left（11 \ overline {2} 0 \ right）として選択された場合）/ \ left [0001 \ right] \）図4に示すように、初期処理段階でチップトップがひどく摩耗し、\（\ overset {\ rightharpoonup} {f_2} \）が重要な役割を果たしました。スクラッチプロセス。したがって、すべり運動は、グローバル座標でYOZ平面と対称的に分布するプリズムすべりシステムで発生します。

<図>

表面/表面下の損傷分布

図6a、bに示すように、\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）および\（（0001）/ \ left [01 \ overline {1 } 0 \ right] \）が選択された場合、スリップモーションは主にスリップシステム\（（0001）/ <1 \ overline {2} 10> \）で発生しました。これは、ツールの前方への押し出しによるものです。対応するスライド移動モードは、シュミット係数の計算結果と一致しています。表面下の領域にナノ結晶粒子と格子偏向があり、これらの損傷はいくつかの不規則な格子歪みゾーンを形成しました。アモルファス相は機械加工された表面全体を覆い、転位の深さは格子歪み層の深さに近かった。

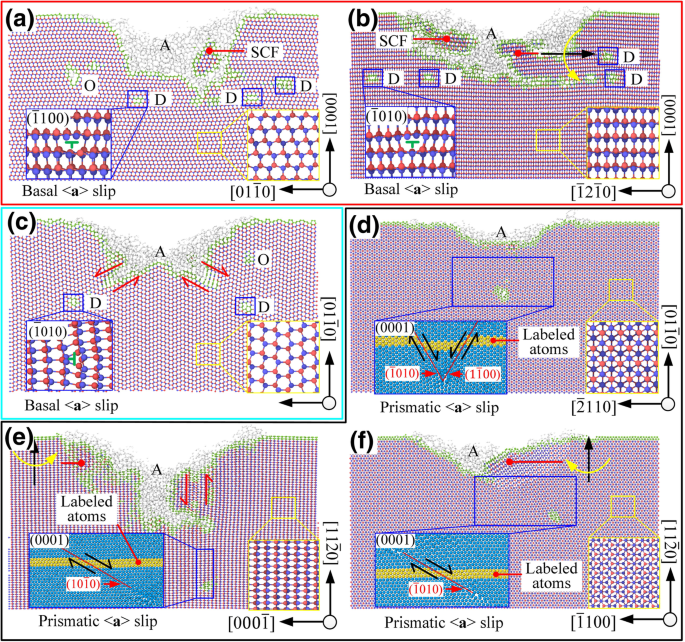
加工領域の断面 D 転位です、 A はアモルファス相、SCFは単結晶形、 O 他のタイプの欠陥であり、 a – f 対応するプロセスモードは\（（0001）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（（0001）/ \ left [10 \ overline {1} 0 \ right ] \）、\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）、\（\ left（01 \ overline { 1} 0 \ right）/ \ left [0001 \ right] \）、\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）、およびそれぞれ\（\ left（11 \ overline {2} 0 \ right）/ \ left [0001 \ right] \）。

基底のシュミット係数として\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）を選択した場合< a >スリップは0に等しく、基本的な< a >理論的にはスリップは発生しないはずです。しかし、荷重方向\（\ overset {\ rightharpoonup} {f_1} \）とすべり方向\（\ left [11 \ overline {2} 0 \ right] \）の間の角度はわずか5.3°でした。接触領域と非接触領域の間の相対運動によるせん断作用の下で（​​図6cを参照）、基底< a >スリップは、\（\ left（01 \ overline {1} 0 \ right）/ \ left [2 \ overline {1} \ overline {1} 0 \ right] \）の処理モードでプリズムスリップの前にトリガーされました。 V溝の両側で発生しました。 \（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）の処理モードでは、荷重方向間の角度\（\ overset {\ rightharpoonup } {f_1} \）とスライド方向\（\ left [1 \ overline {2} 10 \ right] \）と\（\ left [\ overline {1} \ overline {1} 20 \ right] \）はそれぞれ24.7°と35.3°。剪断作用は、基底面の滑り運動を誘発しなかった。対応するすべり運動モードは、シュミット係数の計算結果と一致しています。図6eに示すように、\（\ left（11 \ overline {2} 0 \ right）/ \ left [1 \ overline {1} 00 \ right] \）を選択すると、スリップシステム\（\ left [ 1 \ overline {2} 10 \ right] / \ left（\ overline {1} 010 \ right）\）は、\（\ overset {\ rightharpoonup} {f_1} \）と\の共同作用の下で高いシュミット係数を持っていました（\ overset {\ rightharpoonup} {f_2} \）、これは必然的に地下損傷層の深さを大きくします。格子歪みとアモルファス相も存在しましたが、基底面での加工とは異なり、転位の深さは格子歪みの深さよりも大幅に大きかった。 sp ³ → sp ² 遷移挙動は地下領域で発生しました。

処理方向が c と平行な場合 -軸、チップの激しい摩耗により、下向きの押し出しによって引き起こされる角柱状の滑りが、安定した引っかき段階での主要な滑り運動モードでした。対応するすべり運動モードはシュミット係数の計算結果と一致していた。 \（\ left（01 \ overline {1} 0 \ right）/ \ left [0001 \ right] \）が選択され、荷重方向が\（\ overset {\ rightharpoonup} {f_2} \）の場合、スリップシステム\（\ left [1 \ overline {2} 10 \ right] / \ left（\ overline {1} 010 \ right）\）および\（\ left [\ overline {1} \ overline {1} 20 \ right] / \ left（1 \ overline {1} 00 \ right）\）は同じシュミット係数を持ち、2つのすべり面で60°の角度で横滑りが発生し、その後、ピン止め効果が発生してすべり運動が妨げられました。 。したがって、最大地下損傷深度 SSD _max h 以下になります _t tan θ / 2コットα / 2、ここでθ =101°はナノグルーブの理論上の角度であり、α=60°はすべり面\（\ left（\ overline {1} 010 \ right）\）と\（\ left（1 \ overline {1} 00 \ right）\）。 \（\ left（11 \ overline {2} 0 \ right）/ \ left [0001 \ right] \）を選択した場合、すべりシステム\（\ left [\ overline {2} 110 \ right] / \ left（ 0 \ overline {1} 10 \ right）\）と\（\ left [1 \ overline {2} 10 \ right] / \ left（\ overline {1} 010 \ right）\）も同じシュミット係数を持っていました。しかし、すべり運動は先端の不規則な摩耗の影響を受け、すべりシステム\（\ left [1 \ overline {2} 10 \ right] / \ left（\ overline {1} 010 \ right）\）のみが発生しました。

要約すると、図7に示すように、さまざまな処理条件下での表面下領域の損傷は、主に転位、格子歪み（ねじれ/相対滑り）、およびアモルファス相でした。 6H-SiCの変形は、主にスリップ運動、材料の非結晶化、および不規則な格子歪みによって引き起こされました。主なすべり変形モードは、加工面/方向に密接に関連する基底すべりと角柱すべりでした。

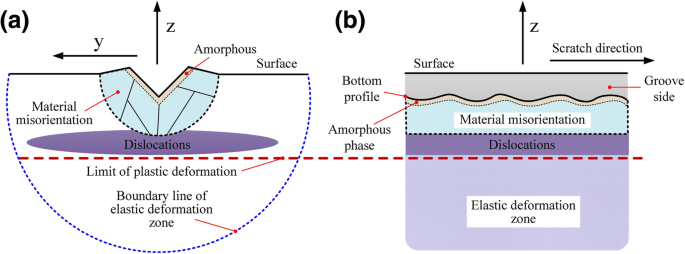
処理された表面/表面下の損傷フォームの分布。 a xy 断面。 b xz 断面