単一のMoS2格子を使用した二軸ひずみセンサー
要約
この論文では、新しいタイプのMoS 2 を報告します。 〜1‰の精度限界を持つ面内二軸ひずみゲージ用のベースの格子センサー。 MoS 2 グレーティングは、最大5%のさまざまな2軸ひずみで数値的にシミュレートされます。第一原理計算により、MoS 2 のひずみ感度が明らかになりました。 反射スペクトルは、グレーティング構造と統合された追加のひずみセンサーと見なすことができ、面内の2軸ひずみのマッピングを可能にします。プロトタイプMoS 2 に関する実験的研究 -グレーティングセンサーは、グレーティング周期に垂直なひずみ成分がグレーティングの1次回折パターンに強度ピークシフトを引き起こす可能性があることをさらに確認します。この作業は、単一の格子デバイス内の面内二軸ひずみの検出に向けた新しい道を開きます。私たちの新しいアプローチは、二軸ひずみ下で予測可能な反射応答を持ち、2次元単結晶層を形成する能力を持つ他の材料に適用できます。
はじめに
フレキシブルエレクトロニクス技術は、学術界や産業界から広く注目されていますが、動的変位と変形の監視が困難なため、マイクロスケールおよびナノスケールのフレキシブルデバイスの設計と応用は困難です[1,2,3,4,5]。抵抗ひずみゲージに基づくほとんどの従来のひずみ検出方法は、小型のセンサーアレイを必要とします[4、6、7]。これは、フレキシブル電子アプリケーション用に製造するのは困難です。スペックル干渉法などの光学ベースの2次元(2D)ひずみ検出技術は、精度が高いため、ピエゾ抵抗に基づく技術よりも優れています[8]。しかし、彼らの画像相関測定戦略は、複雑な画像処理技術の要件によって挑戦されています[8、9、10]。反射型回折格子は、ひずみ測定に高解像度を提供できますが、単一のデバイス内で2Dひずみを検出する機能がありません[11]。
過去数年間、2D素材は多大な研究努力を集めてきました。書記素[12、13]の導入に続いて、2D材料のファミリーは、2原子の薄い黒リン[14]、3原子の薄い遷移金属ジカルコゲナイド[15]、4原子の薄いグループIIIなどの多くの新しいメンバーによって拡大されました。金属モノカルコゲナイド[16]、およびその他の非層状2D材料[17]。これらの材料には多くの興味深い特性が見られ、材料科学のスポットライトの下に置かれています[18、19、20、21、22、23、24]。
遷移金属ジカルコゲナイドは、優れた光学的および機械的特性を示します[25、26、27]。たとえば、MoS 2 反射率変調[28]を伴う2軸ひずみの19.5%[26]に耐えることができ、WSe 2 ひずみ工学を介して、顕著なベリー曲率双極子と非線形ホール効果を示すことができます[29]。材料の反射スペクトルのひずみ感度を反射格子デバイスの機能に組み込むことは、単一デバイス内の二軸検出にひずみ測定を拡張する効率的な方法になります。ただし、2Dひずみ検知アプリケーション用のひずみ誘起材料反射率変調と組み合わせた反射格子の報告はありません。
ここでは、MoS 2 のひずみ感度を含む新しいタイプの面内二軸ひずみ検出技術を提案します。 反射型回折格子センサーの反射率。第一原理計算により、二軸ひずみがMoS 2 の回折パターンの強度分布のピークをシフトさせる可能性があることが明らかになりました。 MoS 2 の反射率のため、ベースのグレーティングデバイス ひずみによる変形に敏感です。この非線形ピークシフトは、一次ひずみ線形方程式に2次項を追加することでよく示されます。この方程式から、格子周期方向に垂直なひずみ成分を〜1‰の精度で抽出できます。プロトタイプMoS 2 に関する実験的研究 -グレーティングデバイスは、グレーティング周期に垂直なひずみがグレーティングの1次回折パターンの強度ピークシフトを引き起こす可能性があることを確認します。私たちの調査によると、単一の格子センサーを備えたワンショットの面内二軸ひずみゲージの可能性が示されています。
メソッド
MoS 2 の理論計算 フレーク
MoS 2 ひずみに対する光学的応答はすべて、Vienna Ab-initio Simulation Package(VASP)[30]を使用して実行される第一原理計算によって研究されます。全電子プロジェクター拡張波(PAW)ポテンシャル[31]がすべての計算に使用されました。幾何学的緩和と静的計算は、Perdew-Burke-Ernzerhof(PBE)一般化勾配近似(GGA)法を使用して実行されました[32]。スピン軌道相互作用(SOC)[33]も静的計算に含まれていました。光学特性を決定するために、準粒子エネルギーは最初にグリーン関数理論から導出されたGW法によって得られました[34]。静的計算から得られた波動関数とGW計算からの準粒子エネルギーを使用して、誘電率を予測するためのベーテサルピーター方程式(BSE)計算[35]を実行しました。
バルク結晶モデルを使用して、MoS 2 を表現しました。 フレーク(5層を超えるスタック間の光学特性の違いはごくわずかです[36])。最適化の計算では、エネルギーカットオフを400 eVに設定し、15 * 15 * 4のMonkhorst–Packkポイントセットを使用してブリルアンゾーンをサンプリングしました。格子定数は、歪んだMoS 2 を後で計算するための参照として最初に最適化されました。 フレーク。最適化された格子定数は a = b =3.18Åおよび c =13.87Å。エネルギーが10 –5 に収束するまで、ジオメトリは緩和されました。 eV。以前の文献[37]の手法を採用し、300eVおよび k のエネルギーカットオフ 光学計算では、6×6×2のポイントセットを使用しました。静的エネルギーは10 –6 に収束しました すべての計算でeV。回折パターンは、ヘルムホルツ-キルヒホッフの定理[38]に基づいてシミュレートされました。詳細については、追加ファイル1を参照してください。
MoS 2 の準備 スペクトル測定のサンプル
MoS 2 薄膜は、市販のMoS 2 から機械的に剥離されました。 単結晶(SPIサプライ)およびテープでポリジメチルシロキサン(PDMS)基板に転写されます。転写後、接着性を高めるためにフレークと基板上にPDMSの別の層が製造されました。
MoS 2 の準備 フレキシブル基板の格子
MoS 2 薄膜は、市販のMoS 2 から機械的に剥離されました。 単結晶(SPIサプライ)およびテープでポリジメチルシロキサン(PDMS)基板に転写されます。グレーティングデバイスを製造するには、MoS 2 フレークは、最初に電子ビームリソグラフィー(EBL)によって格子構造にパターン化されました。次に、パターン化されたサンプルを20 Wの電力の酸素プラズマでエッチングしました。最後に、MoS 2 を取得しました。 PMMAを洗い流すことによるベースのグレーティングデバイス。
MoS 2 デバイス測定
スーパーコンティニウム白色光源(NKT Photonics SuperK Compact)は、励起レーザーとして使用されます。励起レーザーは、図1に示すように、1つの開口部を通過し、サンプル平面に対して特定の角度でフレークサンプルまたはグレーティングサンプルに当たります。反射率測定では、反射されたレーザーは、分光計に接続された光ファイバを介して収集されます。さまざまなひずみの下での反射スペクトルは、分光計によって測定されたデータから計算されます。 MoS 2 をテストするには グレーティングでは、反射されたレーザーがホワイトボードに投影され、長い楕円形の光スポットとして表示されます。光点の写真は、強度分布を分析するために使用されます。
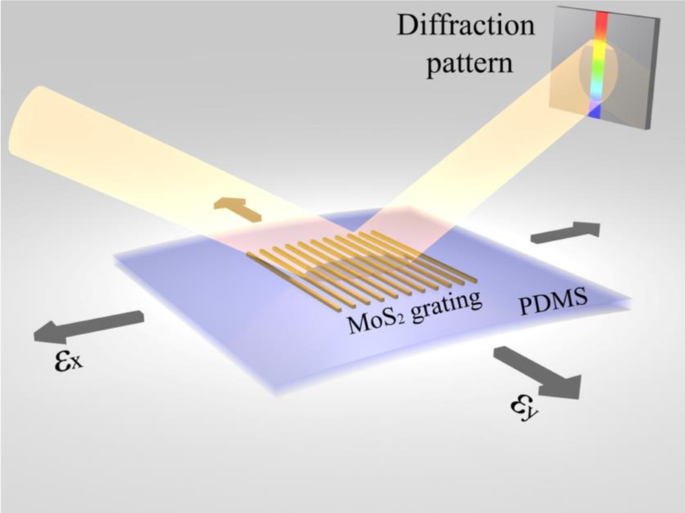
MoS 2 の概略図 二軸ひずみゲージ用のPDMSのフレキシブル基板上のベースの格子センサー
結果と考察
従来の反射型回折格子センサーでは、平行な回折格子ストリップの周期構造が光を回折することができ、回折パターンの位置シフトを監視することにより、回折を利用して回折格子の周期方向に沿ったひずみを測定します[11]。周期的な構造の向きにより、反射型回折格子のひずみ検出機能は、面内の一軸ひずみゲージ(周期的な方向に平行)に制限されます。面内二軸ひずみゲージで使用するために反射格子機能を拡張するために、材料の反射率のひずみ感度など、格子材料の固有の光学特性を、で検出する追加のひずみセンサーと見なすことができることを提案します。 -周期方向に垂直な平面ひずみ成分。
MoS 2 層状構造を持っています:S原子の2つの層の間に挟まれたMo原子の層。層間の相互作用は弱いファンデルワールス力です。ここでは、MoS 2 を設計します フレークベースの反射型回折格子センサー(図1)を使用して、第一原理計算により、さまざまな面内二軸ひずみ下でのデバイスの回折パターンを調査します。計算での入射ビームの波長範囲は400〜850nmです。回折格子は次のように説明できます:
$$ d \ left(\ mathrm {sin} {\ theta} _ {i}-\ mathrm {sin} {\ theta} _ {m} \ right)=n \ lambda $$(1)ここで、\(d \)は2つの隣接する回折格子ストリップ間の距離です。\({\ theta} _ {i} \)は入射ビームと回折格子の法線の間の角度\({\ theta} _ {m } \)は、回折ビームが最大値であるときの回折ビームと法線の間の角度です。 n は回折次数、\(\ lambda \)はビーム波長です[11]。式から(1)、異なる\(\ lambda \)を持つ入射ビームは異なる\({\ theta} _ {m} \)を持たなければならないことがわかります。したがって、連続波長ビームは、異なる\({\ theta} _ {m} \)に対応する連続した一連の回折スポットを引き起こし、楕円形の一次回折パターンを形成します。
図2aは、ひずみが加えられていない、設計どおりのグレーティングセンサーの回折パターンのシミュレーション画像を示しています。図2bは、さまざまな2軸ひずみ下でのデバイスのシミュレートされた1次回折パターンの強度ピークとパターン位置の変化を示しています。 850nmの入射ビームに対応する1次回折パターンのエッジには「LW」というラベルが付いています。格子周期方向(\({\ varepsilon} _ {x} \))に沿って面内一軸引張ひずみを加えると、このひずみによって間隔 d が増加する可能性があります。 各ストリップの間。その結果、\({\ theta} _ {m} \)は減少します。これは、\(d \ mathrm {sin} {\ theta} _ {m} \)が任意の\(\ lambda \)に対して一定であり、\が固定されているためです。 ({\ theta} _ {i} \)。したがって、ひずみ\({\ varepsilon} _ {x} \)を0から4.3%に徐々に増やすと、1次回折パターンの各点の位置が0次回折スポットの中心に近づきます。対応するビーム波長と比例関係にあり、これは従来の反射型回折格子センサーの機能と一致しています[11]。
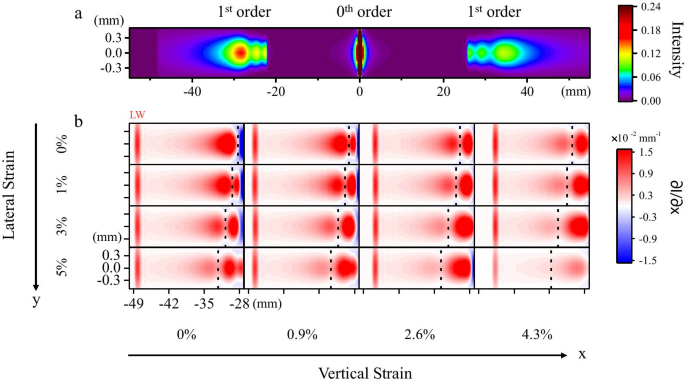
a 回折パターンのシミュレーション画像。ひずみは加えられませんでした。強度は色で表されます。シミュレーションの画面は、反射方向に垂直ではなく、格子に平行に設定されているため、ゼロ次ビームの両側の1次回折スポット間に非対称の動作があります。 b 異なる二軸ひずみ下での1次回折スポットのシミュレーションされた進化。強度偏微分は色で表されます。水平座標と垂直座標は、ゼロ次回折スポットの中心に対する相対的な位置を示します。ピークは破線でマークされています。左から右に、\({\ varepsilon} _ {x} \)はそれぞれ0%、0.9%、2.6%、4.3%に設定されました。上から順に、\({\ varepsilon} _ {y} \)はそれぞれ0%、1%、3%、5%でした
より長い波長の入射ビーム\(\ lambda \)は\({\ theta} _ {m} \)の変動が大きいため、LWエッジの位置シフトが最も顕著になります。ただし、格子周期方向に垂直な面内引張ひずみ(\({\ varepsilon} _ {y} \))を同時に加えると、1次回折パターン内で強度ピークシフトが観察されます。図2bの破線。ひずみ\({\ varepsilon} _ {y} \)が0から5%に増加すると、強度のピークはゼロ次回折スポットの中心からさらに離れてシフトします。強度分布のこのピークシフトは、MoS 2 のひずみ誘起変調に起因すると考えられます。 反射率。以前の文献では、MoS 2 の反射スペクトルが報告されています。 外部ひずみによって調整することができ[28]、反射率は、回折格子の入射ビームに対する回折ビームの強度比に等しくなります。したがって、MoS 2 によって回折されたさまざまな波長のビームの強度 グレーティングは面内ひずみによって変調できます。一方、ひずみ\({\ varepsilon} _ {y} \)はグレーティング周期に影響を与えないため、LWエッジ位置のシフトは発生しません。
図3aは、MoS 2 のピークシフトにおける線形動作を示しています。 MoS 2 の格子ベクトル\({\ varvec {b}} \)に沿った一軸引張ひずみ時の反射スペクトル 適用されます。この一軸引張ひずみにより、MoS 2 でピーク位置の赤方偏移が発生します。 反射率。ただし、面内の2軸引張ひずみを適用すると、反射率のピーク位置シフトに非線形変調が発生します。反射スペクトルのピーク位置と面内二軸引張ひずみの関係は、2次方程式で表すことができます。
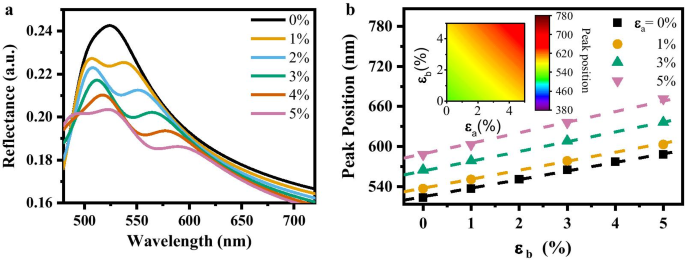
a MoS 2 の反射スペクトル 異なる一軸ひずみ下での波長の関数としてのフレーク。 b MoS 2 の反射スペクトルのピーク位置 異なる二軸ひずみ下のフレーク。破線はフィッティングカーブを表しています。挿入図:フィッティング方程式からのピーク位置のマッピング画像
ここで l 、 m 、および n は3つの定数であり、ε a およびε b MoS 2 の2つの格子ベクトルに沿ったひずみ成分です。 。最初の項は、格子ベクトル\({\ varvec {a}} \)または\({\ varvec {b}} \)に沿った一軸引張ひずみ下でのピーク位置シフトの線形動作を表します。 2番目の項は、2軸引張ひずみ状況での高次の動作を表します。第3項は、歪みのないMoS 2 の反射率のピーク位置です。 。 MoS 2 以降 格子ベクトル\({\ varvec {a}} \)と\({\ varvec {b}} \)は対称的に同等であり、2つの方向に沿った引張ひずみは同じ寄与係数を持ちます。フィッティングの結果は、フィッティング曲線と第一原理で計算されたピーク位置の最大の差が1.76 nmであることを示しています。これは、反射率のピーク位置を使用して計算すると、ひずみゲージの精度の限界が〜1‰になることを示しています。式のひずみ。 (2)。図3bは、近似式から得られたさまざまな面内二軸引張ひずみ下での反射率ピーク位置のマッピング画像を示しています。 (2)(追加ファイル1の反射率の詳細なプロットを参照してください)。
私たちのシミュレーションでは、格子ベクトル\({\ varvec {a}} \)は、シミュレートされた格子の周期方向に垂直です。したがって、ひずみ\({\ varepsilon} _ {y} \)は\({\ varepsilon} _ {a} \)に等しく、ひずみ\({\ varepsilon} _ {x} \)は\(\)に等しくなります。 sqrt {3} / 2 \ times {\ varepsilon} _ {b} \)。私たちの計算によると、MoS 2 ベースのグレーティングセンサーである面内ひずみ\({\ varepsilon} _ {x} \)は、1次回折パターンのLWエッジ位置シフトによって測定できます。一次回折パターンの強度ピークシフトに基づいて、二次式を利用することができます。 (2)ピークシフトから面内ひずみ\({\ varepsilon} _ {x} \)の寄与を差し引く。次に、面内ひずみ\({\ varepsilon} _ {y} \)。
を定量的に計算できます。MoS 2 のひずみ感受性をさらに実験的に研究する 反射率、MoS 2 を機械的に剥離しました フレーク(数十ナノメートルの厚さ。詳細は追加ファイル1を参照)を使用し、乾式転写法(図4aの挿入図に示す)によってフレークをポリジメチルシロキサン(PDMS)の柔軟な基板に取り付けました。この製造されたMoS 2 に面内一軸引張ひずみが加えられました。 基板の2つの側面を2つの並進ステージに固定し、基板を伸ばすことによってデバイス。 εを計算することにより、面内一軸引張ひずみを推定しました。 \(=\ delta L / L \)、ここで\(L \)は2つのクリップ間の素材の長さ、\(\ delta L \)は長さの変化です。ひずみが0から4%まで変化すると、MoS 2 のピーク位置の赤方偏移が発生します。 図4aに示すように、反射スペクトル、およびこのシフトの大きさは、理論計算とよく一致しています。図4b、cは、電子ビームリソグラフィーによって製造されたPDMSフレキシブル基板上の2μm周期のMoS2ベースの反射型回折格子センサーの光学画像を示しています(方法の詳細)。 PDMS基板を伸ばすと、周期方向に垂直な面内引張ひずみがMoS 2 に加えられます。 ベースのグレーティングデバイス(図4d)。一次回折パターンの強度分布を監視することにより、強度ピークが、ひずみのない場合と比較して、ゼロ次スポットの中心からさらに離れてシフトすることを観察しました。周期の方向(図4e)。引張ひずみは周期方向に垂直であり、間隔は d であるため、回折パターンの位置シフトは得られません。 各ストリップ間はほとんど変化しません。
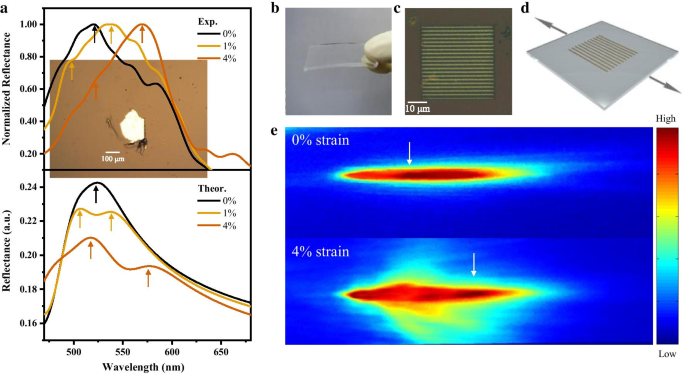
a 一軸ひずみによる反射スペクトルの実験結果(上)、および第一原理計算による一軸ひずみによる反射スペクトル(下)。矢印は、反射率のピーク位置を示しています。挿入図、MoS 2 の光学画像 反射スペクトルテストに使用されるフレーク。 b – c 作製したMoS 2 の光学画像 PDMSのベースの格子。 d MoS 2 の概略図 平行移動ステージによって引き伸ばされたベースの格子。 e 歪みのない(上)および歪みのある(下)グレーティングの1次回折スポットの画像。白い矢印は強度のピークを示します
結論
要約すると、MoS 2 を使用して面内二軸ひずみを測定するための新しい手法を示します。 ベースの反射型回折格子センサー。最大5%のさまざまな二軸ひずみでグレーティングを数値シミュレーションすることにより、概念をテストします。この新しい技術では、周期方向に沿ったひずみ成分を検出するための格子構造(\({\ varepsilon} _ {x} \))が、MoS 2 のひずみ感度と組み合わされています。 周期方向に垂直な面内ひずみ成分を取得するための追加センサーとして機能する反射率(\({\ varepsilon} _ {y} \))。成分\({\ varepsilon} _ {y} \)は、2次近似式と1次回折パターン内の強度ピークシフトを使用して計算されます。理論的な結果は、私たちの実験によって十分に裏付けられています。私たちの仕事は、柔軟な格子センサーの設計への道を開き、単一の格子センサーでワンショット面内二軸ひずみゲージを実現するための新しいアプローチを提供します。私たちのアプローチは、二軸ひずみ下で予測可能な反射応答を持ち、2次元単結晶層を形成する能力を持つ他の材料にも適用できます。
データと資料の可用性
現在の調査中に使用および分析されたデータセットは、合理的な要求に応じて対応する著者から入手できます。
略語
- 2D:
-
二次元
- VASP:
-
ウィーンAb-initioシミュレーションパッケージ
- PAW:
-
全電子プロジェクター増強波
- PBE:
-
Perdew–Burke–Ernzerhof
- GGA:
-
一般化された勾配近似
- SOC:
-
スピン軌道相互作用
- BSE:
-
ベーテ・サルピーター方程式
- PDMS:
-
ポリジメチルシロキサン
- EBL:
-
電子ビームリソグラフィー
ナノマテリアル
- ホームセキュリティ監視のためのRFIDタグの使用
- Raspberry piを使用したTMP006温度センサーPythonライブラリ、
- PythonとRaspberryPiの温度センサー
- InitialStateを使用したppDAQCPiプレートからのセンサーデータのストリーミング
- RaspberryPiを使用したモーションセンサー
- RaspberryPiでのA111パルスレーダーセンサーの使用
- 電気触媒水素発生のための制御された厚さのMoS2
- 電気触媒作用のためのグラフェンナノシート上のMoS2ナノフレークの温度依存性結晶化
- MoS2 / GaAsヘテロ接合における大きな横方向光起電力効果
- 多層MoS2フォトトランジスタのバイアス依存光応答性
- 柔軟なポリ(フッ化ビニリデン)圧電フィルムに基づく超高感度ひずみセンサー



