10進数と2進数
ハッシュマーク、ローマ数字、10進数、2進数の、4種類の記数法を使用して0から20まで数えましょう。
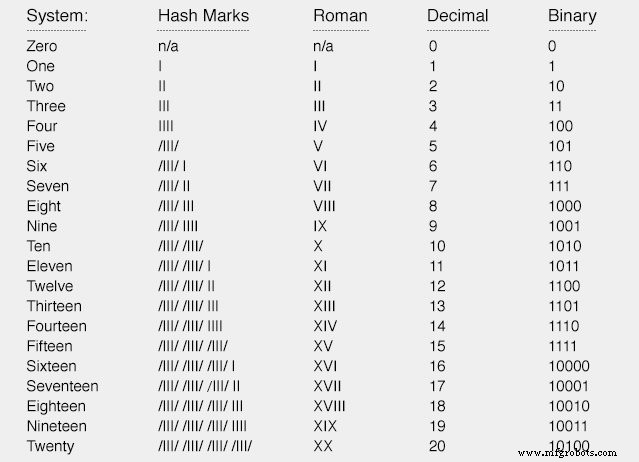
ハッシュマークもローマ数字も、大きな数を象徴するのに非常に実用的ではありません。明らかに、10進数や2進数などの場所加重システムは、タスクに対してより効率的です。
ただし、同じ数の数量に対して、10進表記が2進表記よりもどれだけ短いかに注意してください。 2進表記で5ビットかかるものは、10進表記で2桁しかかかりません。
これは、さまざまな記数法に関して興味深い質問を提起します。限られた数の暗号位置または場所で、どれだけの数を表すことができるでしょうか。粗ハッシュマークシステムでは、整数ステップごとに1つのハッシュマーク「場所」が必要なため、場所の数は表現できる最大の数です。
ただし、場所に重み付けされた記数法の場合、答えは、記数法(10進数の場合は10、2進数の場合は2)に基づいて、桁数の累乗にするとわかります。
たとえば、10進法の5桁は、0から99,999(10の5乗=100,000)までの100,000の異なる整数値を表すことができます。 2進数システムの8ビットは、0〜11111111(2進数)または0〜255(10進数)の256の異なる整数値を表すことができます。これは、2の8乗が256に等しいためです。
数値フィールドに場所の位置が追加されるたびに、数値を表す能力は基数の係数で増加します(10進数の場合は10、2進数の場合は2)。
このトピックの興味深い脚注は、最初の電子デジタルコンピュータの1つであるEniacです。
Eniacの設計者は、2進数の記数法を使用するのではなく、「リングカウンター」と呼ばれる一連の回路を使用して、数値を10進数でデジタル表現することを選択しました。これは、非常に表現および計算するために必要な回路の数を最小限に抑えるためです。多数。
このアプローチは逆効果であることが判明し、それ以降、事実上すべてのデジタルコンピュータは純粋にバイナリ設計になっています。
2進数から10進数への変換
2進数の数値を10進数形式の同等の数値に変換するには、ビットとそれぞれの場所の重み定数のすべての積の合計を計算するだけです。説明のために:

右端のビットは、最下位ビット(LSB)と呼ばれます。これは、最も低い重み(1つの場所)の場所にあるためです。
左端のビットは、最上位ビット(128の位)にあるため、最上位ビット(MSB)と呼ばれます。
「1」のビット値は、それぞれの場所の重みが合計値に追加されることを意味し、「0」のビット値は、それぞれの場所の重みが ないことを意味することを忘れないでください。 合計値に追加されます。上記の例では、次のようになります。
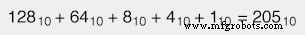
小数点の代わりに「2進ポイント」と呼ばれるドット(。)の付いた2進数に遭遇した場合、同じ手順に従い、ポイントの右側の各桁の重みが値の半分であることに気付きます。その左側に1つ(各桁が小数点の右側に重みがあるのと同じように) ポイントは、その左側にあるものの10分の1の重量です)。例:

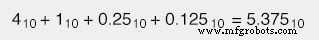
関連するワークシート:
- バイナリ数学ワークシート
産業技術



