ド・モルガンの定理

DeMorganという名前の数学者は、ブール代数のグループ補完に関する2つの重要なルールを開発しました。

グループ 補完、私は複数の変数の上の長いバーで表される用語のグループの補完を指します。

論理ゲートの章から、ゲートへのすべての入力を反転すると、そのゲートの基本的な機能がANDからORに、またはその逆に反転し、出力も反転することを思い出してください。

したがって、すべての入力が反転されたORゲート（負のORゲート）はNANDゲートと同じように動作し、すべての入力が反転されたANDゲート（負のANDゲート）はNORゲートと同じように動作します。

>

ド・モルガンの定理は、「逆方向」の形式で同じ同等性を示しています。つまり、任意のゲートの出力を反転すると、入力が反転した反対のタイプのゲート（AND対OR）と同じ機能になります。

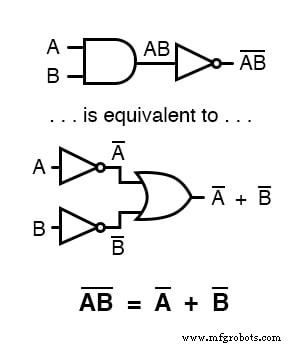
ABという用語にまたがる長いバーは​​、グループ化記号として機能するため、AとBを個別に反転した積とはまったく異なります。

つまり、（AB） ’はA’B’と等しくありません。 「プライム」記号（ ’）は、バーのように2つの変数にまたがることができないため、前の文の用語AB全体に適用するために括弧を使用する必要があります。

ただし、バーは、複数の変数にまたがる場合、独自のグループ化シンボルとして機能します。

これは、後で説明するように、ブール式の評価と削減の方法に大きな影響を与えます。

ドモルガンの定理

ド・モルガンの定理は、破壊の観点から考えることができます。 長いバーの記号。

長いバーが壊れると、ブレークの真下の操作が加算から乗算に、またはその逆に変わり、壊れたバーの断片は個々の変数の上に残ります。説明のために：

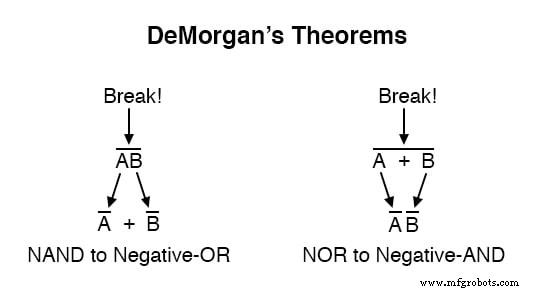
1つの式に複数のバーの「レイヤー」が存在する場合、一度に1つのバーしか分割できません 、そして一般的に、最も長い（一番上の）バーを最初に壊すことで単純化を開始する方が簡単です。

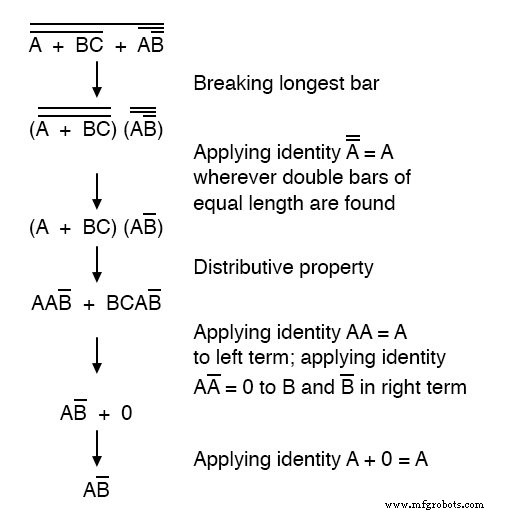
説明のために、式（A +（BC） ’）’を取り、ド・モルガンの定理を使用してそれを減らしましょう：

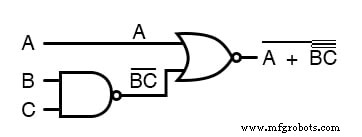
最初に最も長い（最上部の）バーを壊すというアドバイスに従って、最初のステップとして、式全体をカバーするバーを壊すことから始めます。

その結果、元の回路は、A入力が反転した3入力ANDゲートに縮小されます。

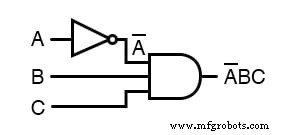
絶対にしないでください ここに示すように、1つのステップで複数のバーを分割します：

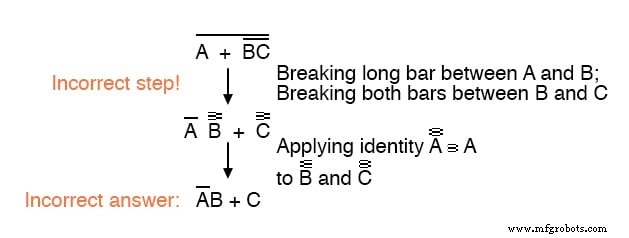
ステップを節約し、一度に複数のバーを壊したくなるかもしれませんが、それはしばしば間違った結果につながるので、それをしないでください！

長いバーを最初に分割するのではなく、短いバーを最初に分割することで、この式を適切に減らすことができます。

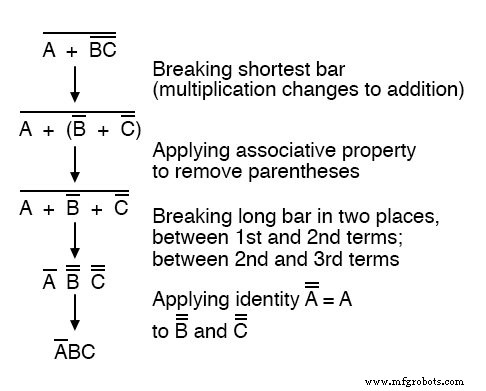
最終結果は同じですが、最も長いバーが最初に壊れた最初の方法を使用する場合と比較して、より多くの手順が必要になります。

3番目のステップで、長いバーを2か所で壊したことに注意してください。

これは正当な数学演算であり、1つのステップで2つのバーを壊すのと同じではありません！

1つのステップで複数のバーを壊すことの禁止はではありません 複数の場所でバーを壊すことの禁止。

複数の場所に侵入する 単一のステップで大丈夫です。複数のバーを壊す 単一のステップではありません。

次のステップで括弧を削除したことを考えると、なぜ括弧が部分式B ’+ C’の周りに配置されたのか疑問に思われるかもしれません。

これは、ド・モルガンの定理の重要であるが無視されやすい側面を強調するために行いました。

長いバーは​​グループ化シンボルとして機能するため、以前は壊れたバーによってグループ化されていた変数は、適切な優先順位（操作の順序）が失われないようにグループ化されたままにする必要があります。

この例では、短いバーを壊した後に括弧を入れるのを忘れても問題ありませんが、そうでない場合はそうなる可能性があります。

別の式から始めて、この例を考えてみましょう：

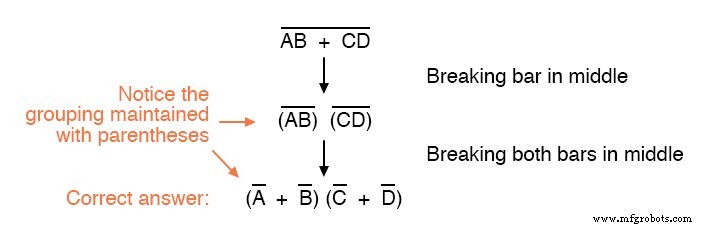
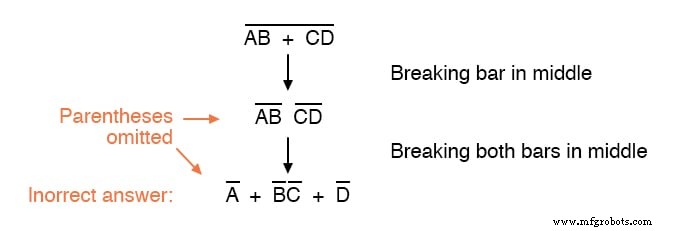
ご覧のとおり、正しい答えを得るには、この式の補完バーによって示されるグループ化を維持することが重要です。

ド・モルガンの定理の原理をゲート回路の単純化に適用してみましょう。

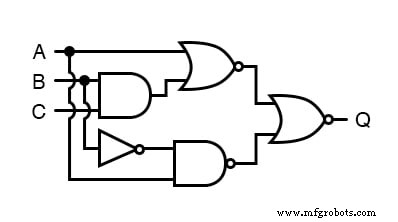
いつものように、この回路を単純化するための最初のステップは、同等のブール式を生成することでなければなりません。

これを行うには、入力がわかったときに、各ゲートの出力に部分式ラベルを配置します。このプロセスの最初のステップは次のとおりです。

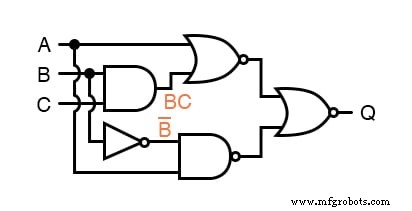
次に、最初のNORゲートとNANDゲートの出力にラベルを付けることができます。

逆出力ゲートを扱う場合、ゲートの出力の式を なしで作成する方が簡単だと思います。 最後の反転。矢印は反転バブルの直前を指しています。

次に、ゲートから出ているワイヤー（バブルの後）に、完全で補完的な表現を書きます。

これにより、式の作成タスクを2つのステップに分割するように強制することで、部分式の補完バーを忘れないようにすることができます。

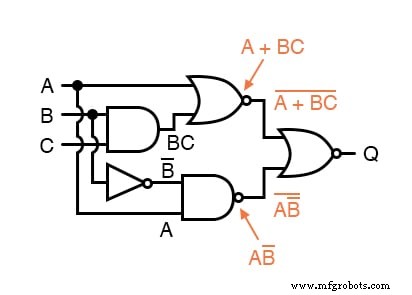
最後に、最後のNORゲートの式（または式のペア）を記述します。

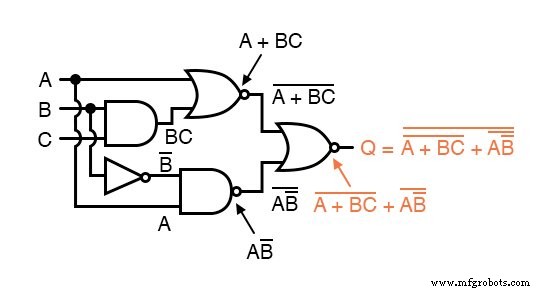
ここで、ブール代数の恒等式、プロパティ、規則、および定理（DeMorgan’s）を使用して、この式を減らします。

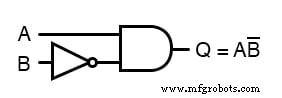
この非常に単純化された式の等価ゲート回路は次のとおりです。

レビュー：

• ド・モルガンの定理は、入力が反転したゲートと出力が反転したゲートの間の同等性を説明しています。簡単に言えば、NANDゲートはNegative-ORゲートに相当し、NORゲートはNegative-ANDゲートに相当します。
• ブール式で補完バーを「ブレーク」すると、ブレークの真下の演算（加算または乗算）が逆になり、ブレークされたバーの断片はそれぞれの項に残ります。
• 多くの場合、問題に取り組むには、その下のバーを壊す前に、最も長い（一番上の）バーを壊す方が簡単です。 絶対にしてはいけません 1つのステップで2つのバーを壊してみてください！
• 補完バーはグループ化記号として機能します。したがって、バーが壊れた場合、その下の用語はグループ化されたままでなければなりません。優先順位の変更を避けるために、これらのグループ化された用語の前後に括弧を付けることができます。

関連するワークシート：

• ブール代数ワークシート