真理値表のブール式への変換
デジタル回路を設計する際、設計者は回路が何をすべきかを説明する真理値表から始めることがよくあります。
設計タスクは主に、真理値表に記載されている機能を実行する回路のタイプを決定することです。
真理値表を見て、タスクに必要な論理ゲートまたはリレー論理回路をすぐに想像する自然な能力を持っている人もいますが、残りの人が利用できる手順のテクニックがあります。
ここで、ブール代数は最も劇的な方法でその有用性を証明しています。
この手続き型の方法を説明するために、現実的な設計の問題から始める必要があります。
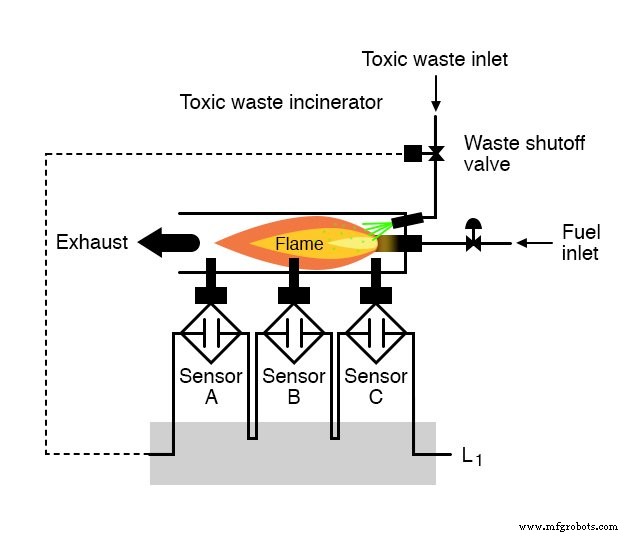
有毒廃棄物焼却炉の火炎検出回路を設計するタスクが与えられたとします。
火の強烈な熱は、焼却炉に持ち込まれた廃棄物の毒性を中和することを目的としています。
このような燃焼ベースの技術は、致命的なウイルスや細菌に感染している可能性のある医療廃棄物を中和するために一般的に使用されています。
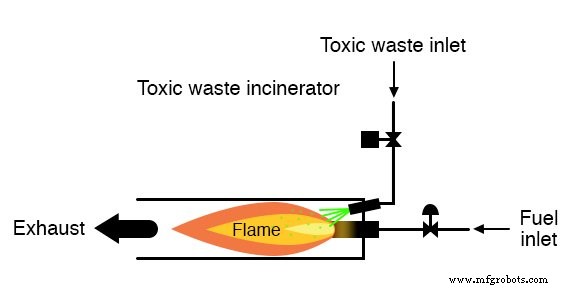
焼却炉内で炎が維持されている限り、廃棄物を焼却炉に注入して中和するのは安全です。
しかし、火炎が消えた場合、燃焼室に廃棄物を注入し続けることは安全ではありません。それは、中和されずに排気ガスから排出され、排気ガスの近くにいる人に健康上の脅威をもたらすからです。
このシステムに必要なのは、炎の存在を確実に検出し、炎が炎検出システムによって「証明」された場合にのみ廃棄物を注入できるようにすることです。
いくつかの異なる火炎検出技術が存在します。光学(光の検出)、熱(高温の検出)、および電気伝導(火炎経路内のイオン化粒子の検出)であり、それぞれに固有の長所と短所があります。
中和されていない廃棄物をこの焼却炉の排気口に排出する可能性があるため、危険度が高いため、単一のセンサーの故障が発生しないように、火炎検出システムを冗長化(複数のセンサー)することが決定されたとします。排気ガスからの毒素の放出に。
各センサーには、ロジックシステムの入力をアクティブにするために使用するノーマルオープン接点(炎がない場合は開き、炎が検出された場合は閉じます)が装備されています。
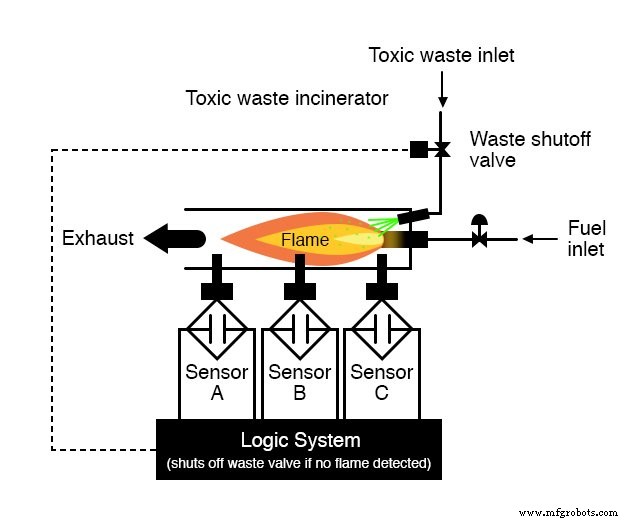
私たちの仕事は、センサーによって証明された良好な炎がある場合にのみ、廃液バルブを開くように論理システムの回路を設計することです。
ただし、最初に、この制御システムの論理的な動作を決定する必要があります。
3つのセンサーのうち1つだけが炎を検出した場合に、バルブを開きますか?おそらくそうではありません。これは、複数のセンサーを持つという目的を損なうためです。
センサーのいずれかが、炎がないときに炎の存在を誤って示すような方法で故障した場合、「炎を示す3つのセンサーのうちの1つ」の原理に基づく論理システムは、同じ出力を提供します。単一センサーシステムでも同じ障害が発生します。
はるかに優れた解決策は、 3つのセンサーすべての場合にのみバルブが開くように命令されるようにシステムを設計することです。 良い炎を検出します。
このように、炎を誤って示している単一の故障したセンサーは、バルブを開いた位置に保つことができませんでした。むしろ、この危険な状態が発生するためには、3つのセンサーすべてが同じ方法で故障する必要があります(非常にありそうもないシナリオです)。
したがって、真理値表は次のようになります。
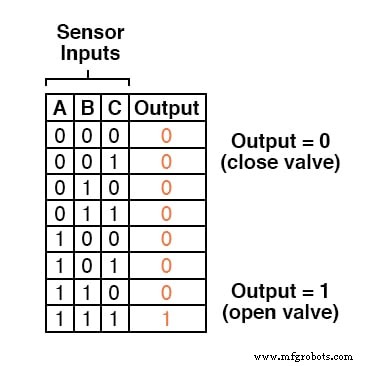
この機能が3入力ANDゲートで生成できることを理解するのに多くの洞察は必要ありません。入力A AND の場合に限り、回路の出力は「ハイ」になります。 入力B AND 入力Cはすべて「高」です:
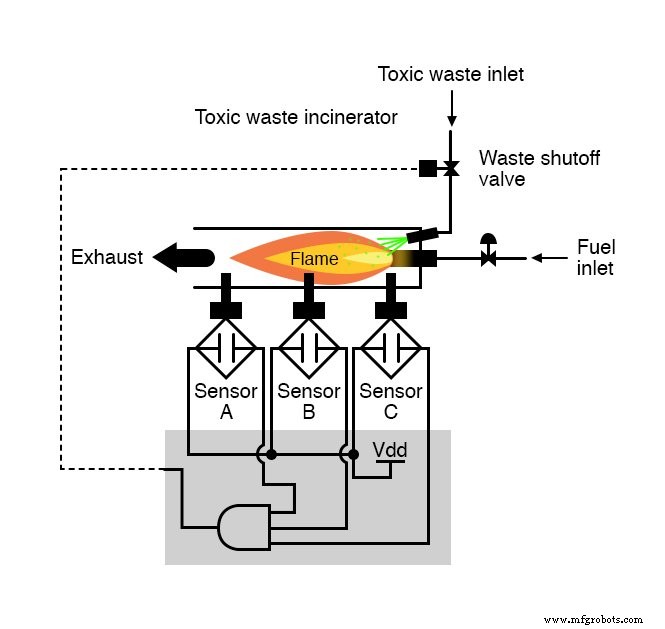
リレー回路を使用する場合は、3つのリレー接点を直列に配線するか、3つのセンサー接点を直列に配線するだけで、このAND関数を作成できます。これにより、電力を送って廃液バルブを開く唯一の方法は、3つのセンサーすべてを使用する場合です。炎を示す:
この設計戦略は安全性を最大化しますが、システムは反対の種類のセンサー障害の影響を非常に受けやすくなります。
3つのセンサーの1つが故障して、焼却炉の燃焼室に実際に良好な炎があったときに炎がないことを示したとします。
その1回の障害で廃棄物バルブが不必要に遮断され、生産時間が失われ、燃料が無駄になります(廃棄物の焼却に使用されていなかった火を供給します)。
システムを不必要にシャットダウンすることなくこの種の障害を許容し、それでもセンサーの冗長性を提供して、単一のセンサーが「高」に障害が発生した場合(常に炎を示している)の安全性を維持できるロジックシステムがあると便利です。 、検出するものがあったかどうか)。
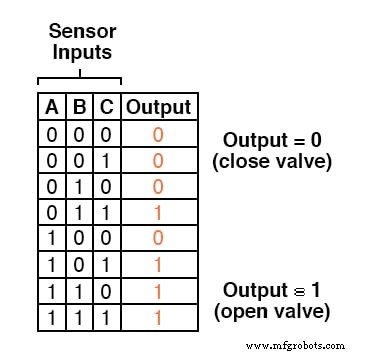
両方のニーズを満たす戦略は、「3つのうち2つ」のセンサーロジックであり、3つのセンサーのうち少なくとも2つが良好な炎を示した場合、廃液バルブが開きます。
このようなシステムの真理値表は次のようになります。
製品の合計の使用
ここでは、どのような論理回路が真理値表を満たすかは必ずしも明らかではありません。
ただし、このような回路を設計するための簡単な方法は、 Sum-Of-Products と呼ばれるブール式の標準形式にあります。 、または SOP 、 形。
ご想像のとおり、Sum-Of-Productsブール式は、文字通り、追加されたブール項のセットです( sumed )一緒に、各用語は乗法( product )ブール変数の組み合わせ。
SOP式の例は、次のようになります。ABC+ BC + DF、積「ABC」、「BC」、および「DF」の合計。
Sum-Of-Products式は、真理値表から簡単に生成できます。
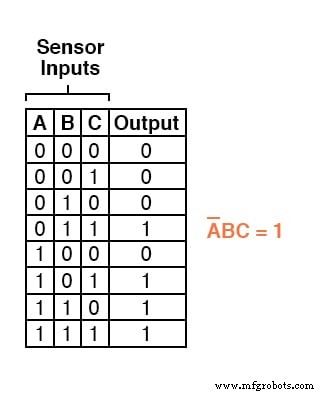
私たちがしなければならないのは、出力が「高」(1)であるすべての行の真理値表を調べ、それらの入力条件が与えられた場合に値1に等しいブール積項を記述することです。
たとえば、A =0、B =1、およびC =1である3つのうち2つの論理システムの真理値表の4行目では、積項はA'BCになります。 A =0、B =1、およびC =1の場合に限り、値は1になります。
真理値表の他の3つの行の出力値は1であるため、これらの行もそれらを表すためにブール積式が必要です。
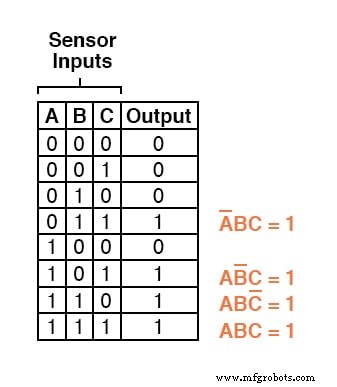
最後に、これら4つのブール積式を加算して結合し、真理値表全体を表す単一のブール式を作成します。
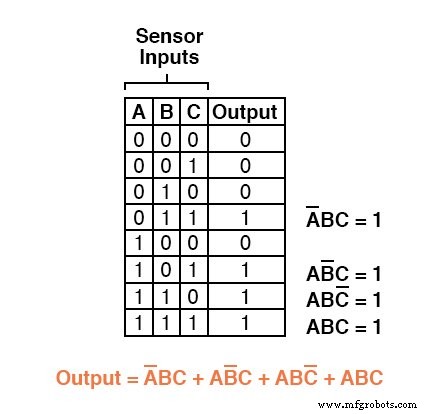
真理値表の関数のブール代数の積の式ができたので、その式に基づいて論理ゲートまたはリレー論理回路を簡単に設計できます。
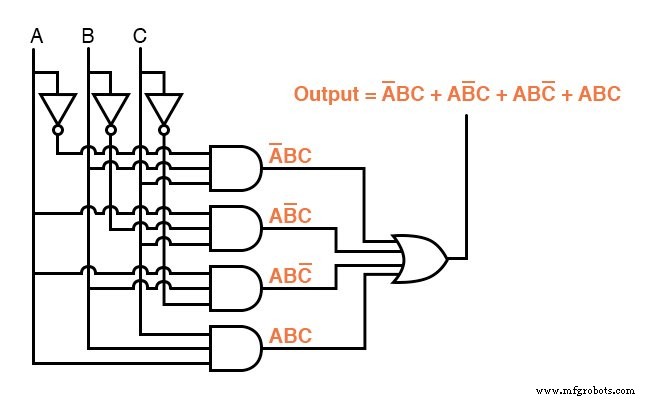
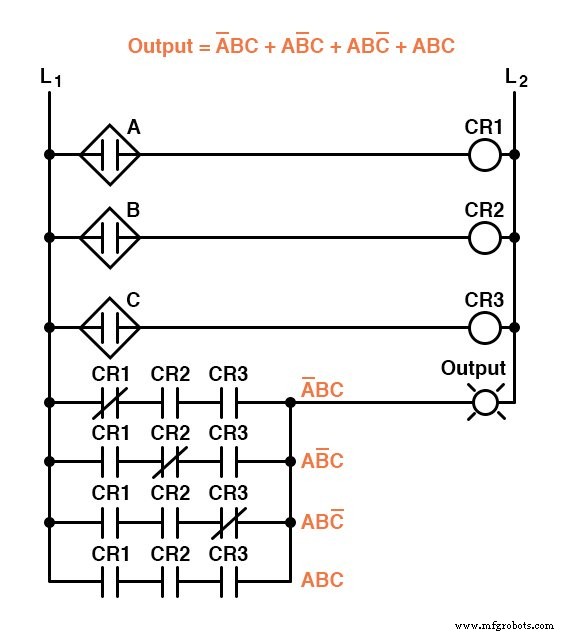
残念ながら、これらの回路はどちらも非常に複雑であり、単純化することでメリットが得られる可能性があります。
ブール代数手法を使用すると、式を大幅に簡略化できます。
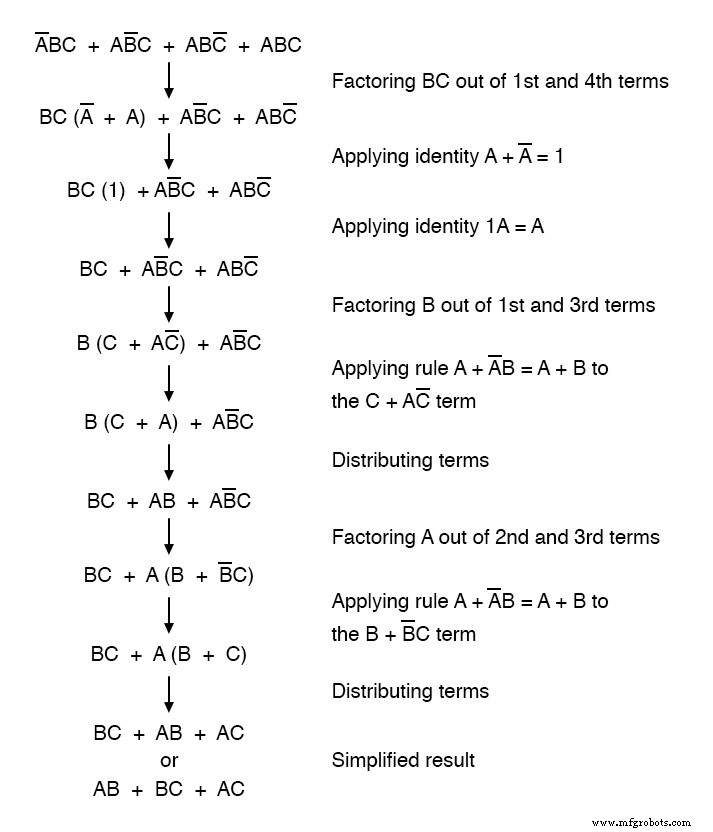
簡略化の結果、ゲート形式またはリレー形式のいずれかで、同じ機能を実行するはるかに単純な論理回路を構築できるようになりました。
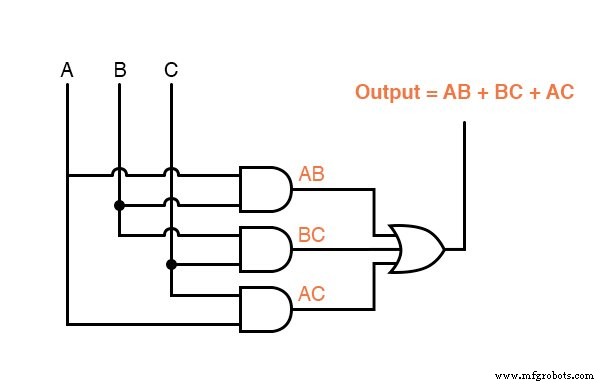
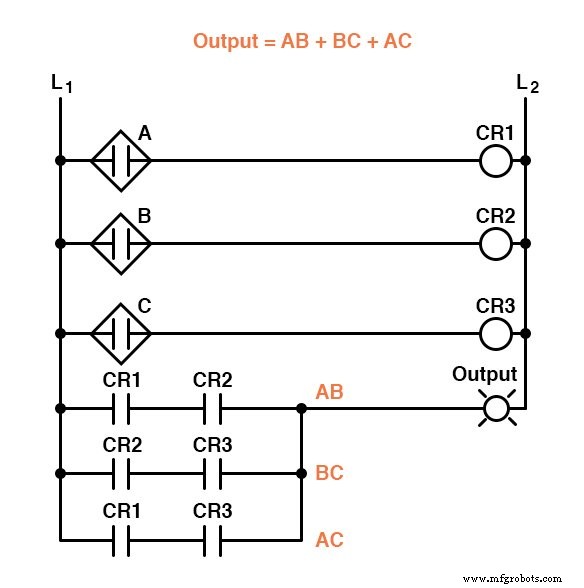
これらの回路のいずれかが、3つの火炎センサーのうち2つからの火炎検証に基づいて、焼却炉の廃液バルブを操作するタスクを適切に実行します。
少なくとも、これは私たちが安全な焼却炉システムを持つために必要なものです。
ただし、センサーのいずれかが他の2つと一致しないかどうかを検出するように設計された論理回路をシステムに追加することで、システムの機能を拡張できます。
3つのセンサーすべてが正常に動作している場合、同じ精度で炎を検出する必要があります。
したがって、それらはすべて「低」(000:炎なし)またはすべて「高」(111:良好な炎)を登録する必要があります。
その他の出力の組み合わせ(001、010、011、100、101、または110)は、センサー間の不一致を構成するため、潜在的なセンサー障害のインジケーターとして機能する場合があります。
6つの「センサーの不一致」状態のいずれかを検出する回路を追加した場合、その回路の出力を使用してアラームをアクティブにすることができます。
焼却炉を監視している人は誰でも、故障した可能性のあるセンサー(入力:011、101、または110)で操作を続行するか、完全に安全であるために焼却炉をシャットダウンするかを判断します。
また、焼却炉が停止していて(炎がない)、1つまたは複数のセンサーがまだ炎(001、010、011、100、101、または110)を示し、他のセンサーが炎がないことを示している場合、明確なセンサーの問題が存在することがわかります。
この「センサーの不一致」検出回路を設計する最初のステップは、その動作を説明する真理値表を作成することです。
「良い炎」の論理回路の出力を説明する真理値表がすでにあるので、別の出力列をテーブルに追加して2番目の回路を表し、論理システム全体を表すテーブルを作成できます。
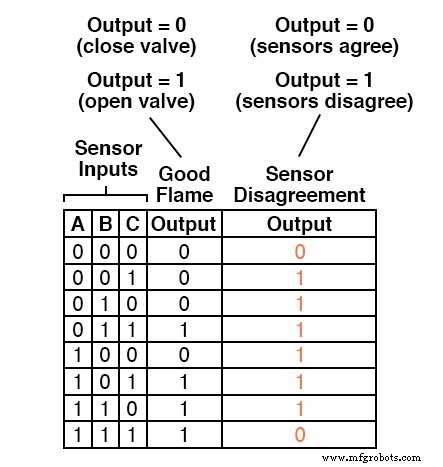
この新しい真理値表の列に対してSum-Of-Products式を生成することは可能ですが、それぞれ3つの変数からなる6つの項が必要になります!
このようなブール式では、単純化するために多くの手順が必要になり、代数エラーが発生する可能性が高くなります。

Product-Of-Sumsの使用
真理値表のすべての「高」(1)出力条件を説明するためにSum-Of-Products式を生成する代わりに、 Product-Of-Sums を生成することもできます。 、または POS 、式、代わりにすべての「低」(0)出力条件を説明します。
最後の真理値表の列に「低」出力のインスタンスがはるかに少ないため、結果のProduct-Of-Sums式に含まれる用語は少なくなります。
その名前が示すように、Product-Of-Sums式は、追加された用語のセットです( sums )、乗算されます( product )一緒に。
POS式の例は、(A + B)(C + D)で、「A + B」と「C + D」の合計の積です。
まず、最後の真理値表の列のどの行に「低」(0)出力があるかを特定し、その行の入力条件に対して0に等しいブール和項を記述します。
たとえば、真理値表の最初の行(A =0、B =0、およびC =0)では、合計項は(A + B + C)になります。これは、その項の値が0であるためです。 A =0、B =0、およびC =0の場合のみ:
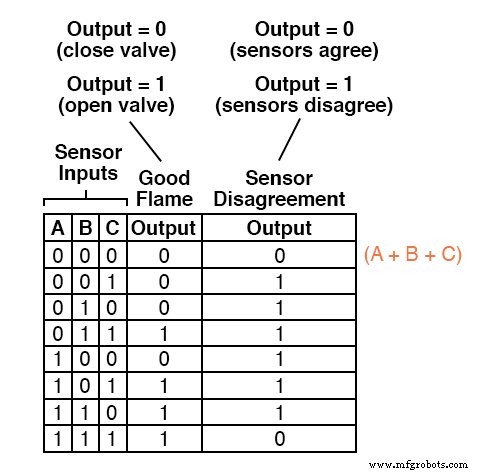
最後の真理値表の列の他の1行だけが「低」(0)出力を持っているので、必要なのは、Product-Of-Sums式を完成させるためのもう1つの合計項です。
この最後の合計項は、A =1、B =1、およびC =1の入力条件に対する0の出力を表します。
したがって、補完されたの合計のみであるため、用語は(A '+ B' + C ')と記述する必要があります。 入力変数は、その条件でのみ0に等しくなります:
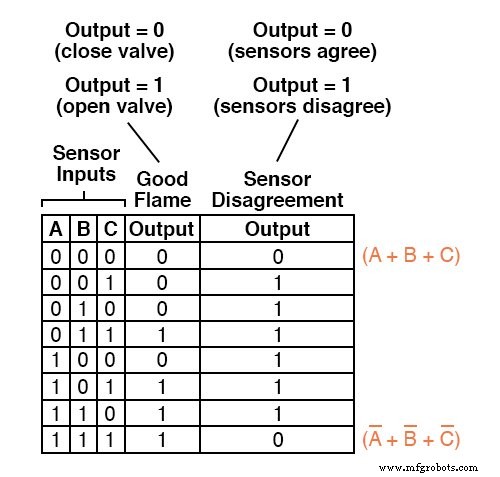
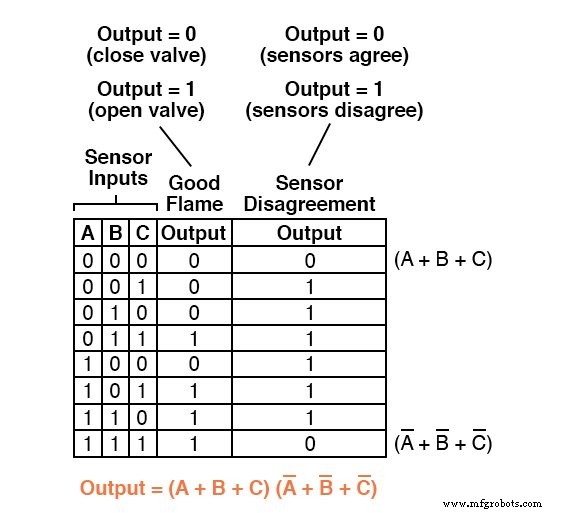
もちろん、完成したProduct-Of-Sums式は、これら2つの合計項の乗法の組み合わせです。
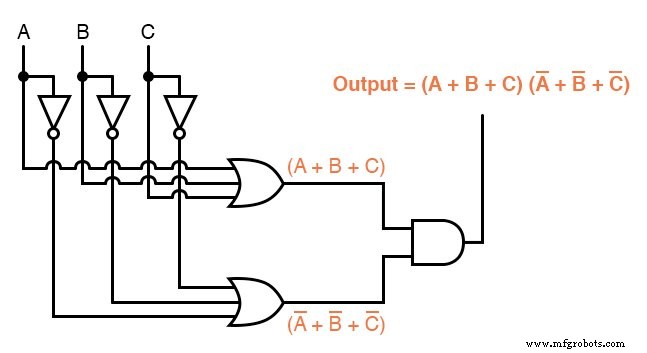
Sum-Of-Products式は、出力が単一のORゲートに接続されたANDゲートのセットの形式で実装できますが、Product-Of-Sums式は、単一のORゲートにフィードするORゲートのセットとして実装できます。 ANDゲート:
これに対応して、Sum-Of-Products式は、直列接続されたリレー接点の並列コレクションとして実装できますが、Product-Of-Sums式は、並列接続されたリレー接点の直列コレクションとして実装できます。
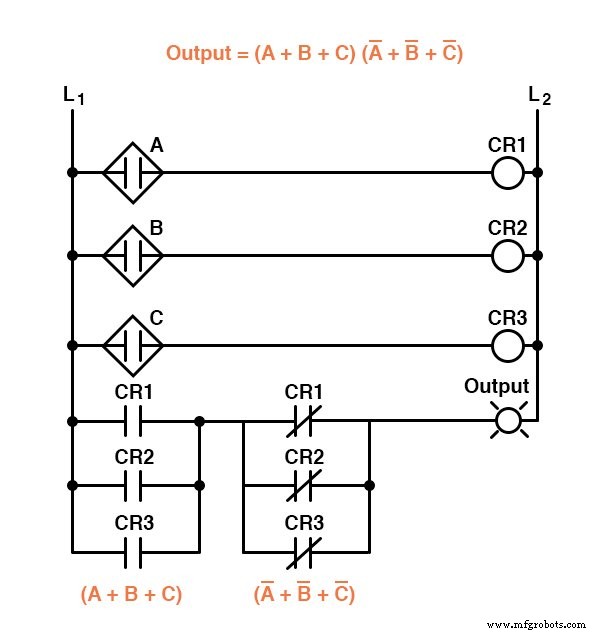
前の2つの回路は、「センサーの不一致」論理回路の異なるバージョンのみを表しており、「良好な火炎」検出回路は表していない。
ロジックシステム全体は、同じ図に示されている「良好な炎」回路と「センサーの不一致」回路の両方の組み合わせになります。
プログラマブルロジックコントローラー(PLC)に実装すると、ロジックシステム全体が次のようになります。
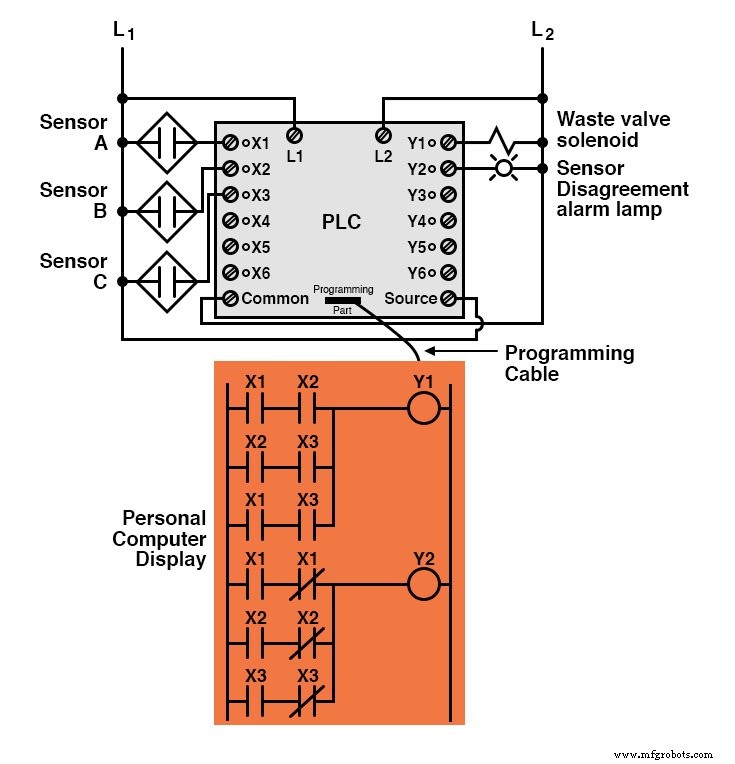
ご覧のとおり、Sum-Of-ProductsとProducts-Of-Sumsの両方の標準ブール形式は、真理値表に適用すると強力なツールになります。
これらを使用すると、真理値表だけからブール式、そして最終的には実際の論理回路を導き出すことができます。これは、論理回路に実行させたいことの仕様書です。
簡単で決定論的な手順を使用して、書面による仕様から実際の回路に移行できるということは、デジタル回路の設計プロセスを自動化できることを意味します。
言い換えれば、真理値表の仕様からカスタム論理回路を設計するようにコンピューターをプログラムすることができます。
真理値表から最終回路までの手順は非常に明確で直接的であるため、それらを実行するために創造性やその他の独自の考えはほとんど必要ありません。
レビュー:
- 製品の合計 、または SOP 、ブール式は、テーブルのどの行に1の出力があるかを判別し、各行に1つの積項を書き込み、最後にすべての積項を合計することにより、真理値表から非常に簡単に生成できます。これにより、真理値表全体を表すブール式が作成されます。
- Sum-Of-Products式は、単一のORゲート(合計)にフィードする一連のANDゲート(製品)としての実装に適しています。
- Product-Of-Sums 、または POS 、ブール式は、テーブルのどの行の出力が0であるかを判別し、各行に1つの合計項を書き込み、最後にすべての合計項を乗算することにより、真理値表から非常に簡単に生成できます。これにより、真理値表全体を表すブール式が作成されます。
- Product-Of-Sums式は、単一のANDゲート(製品)にフィードするORゲート(合計)のセットとしての実装に適しています。
関連するワークシート:
- Sum-of-ProductsおよびProduct-of-Sums式のワークシート
- ブール代数ワークシート
産業技術



