バイナリ加算器

2つのバイナリビットを一緒に追加できるデバイスを構築したいとします。このようなデバイスは半加算器と呼ばれ、そのゲート回路は次のようになります。

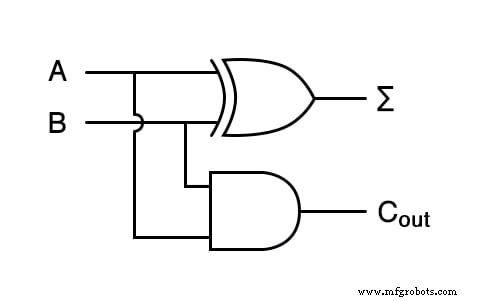
Σシンボルは、半加算器の「合計」出力、つまり合計の最下位ビット（LSB）を表します。 C _out 合計の最上位ビット（MSB）である半加算器の「キャリー」出力を表します。

これと同じ関数をラダー（リレー）ロジックに実装すると、次のようになります。

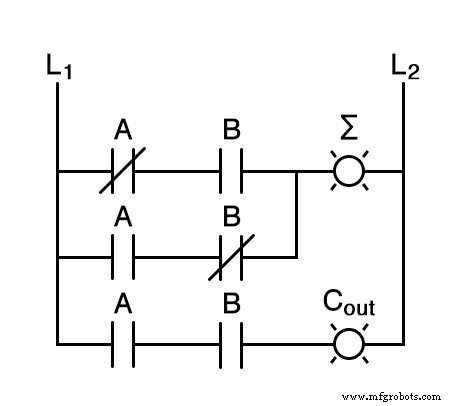
どちらの回路でも、2桁の2進数を加算できます。ビットを足し合わせる方法の数学的「ルール」は、回路のワイヤード論理に固有のものです。

乗算など、バイナリビットを使用して別の算術演算を実行する場合は、別の回路を作成する必要があります。上記の回路設計では、2つのバイナリビットを加算するという1つの機能しか実行されません。それらに何か他のことをさせるには、再配線が必要であり、おそらく別のコンポーネントが必要です。

この意味で、デジタル算術回路は、アナログ算術（オペアンプ）回路と大差ありません。配線されているとおりに動作し、それ以上でもそれ以下でもありません。ただし、この方法でデジタルコンピュータ回路を設計することに限定されるものではありません。

ゲート間の配線接続ではなく、デジタルデータの形式で算術演算の数学的な「ルール」を埋め込むことができます。その結果、比類のない操作の柔軟性が生まれ、まったく新しい種類のデジタルデバイス、プログラム可能なコンピューターが生まれました。。

この章は決して網羅的なものではありませんが、入門教科書で見過ごされがちな2つのデバイス、ルックアップテーブルメモリから始めて、プログラム可能なコンピュータデバイスの性質についてのユニークで興味深い見方を提供します。および有限状態マシン 。

関連ワークシート：

産業技術