複雑な回路
これまでに見た単純な直列構成よりも複雑な回路に遭遇した場合はどうしますか?この回路を例に取ってください:
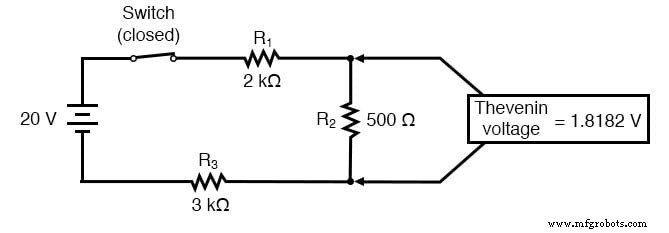
単純な時定数の式(τ=RC)は、コンデンサに接続された単純な直列抵抗に基づいています。さらに言えば、誘導回路の時定数式(τ=L / R)も単純な直列抵抗の仮定に基づいています。では、抵抗がコンデンサ(またはインダクタ)と直並列に接続されているこのような状況で何ができるでしょうか?
テブナンの定理
その答えは、ネットワーク分析の研究から得られたものです。テブナンの定理は、すべてを減らすことができることを示しています いくつかの簡単な手順で、1つの電圧源、1つの直列抵抗、および負荷コンポーネントに相当する線形回路。ここでのシナリオにテブナンの定理を適用するために、無効成分(上記の回路例ではコンデンサー)を負荷と見なし、回路から一時的に取り外して、テブナン電圧とテブナン抵抗を求めます。
次に、テブナンの等価回路値を決定したら、コンデンサを再接続し、これまで行ってきたように、時間の経過に伴う電圧または電流の値を解きます。
コンデンサを「負荷」として識別した後、それを回路から取り外し、負荷端子間の電圧を解きます(もちろん、スイッチが閉じていると仮定します):

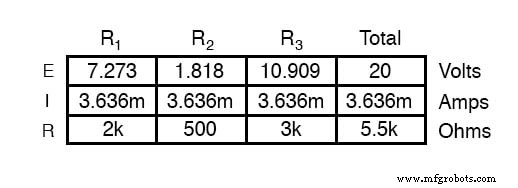
分析のこのステップは、負荷端子間の電圧(抵抗R 2 間の電圧と同じ)を示しています。 )は、負荷が接続されていない状態で1.8182ボルトになります。少し考えてみると、これがコンデンサの両端の最終的な電圧になることは明らかです。完全に充電されたコンデンサが開回路のように動作し、電流がゼロになることを確認してください。この電圧値をテブナン等価回路の電源電圧に使用します。
ここで、テブナン抵抗を解くには、元の回路のすべての電源を削除し、負荷端子から見た抵抗を計算する必要があります。
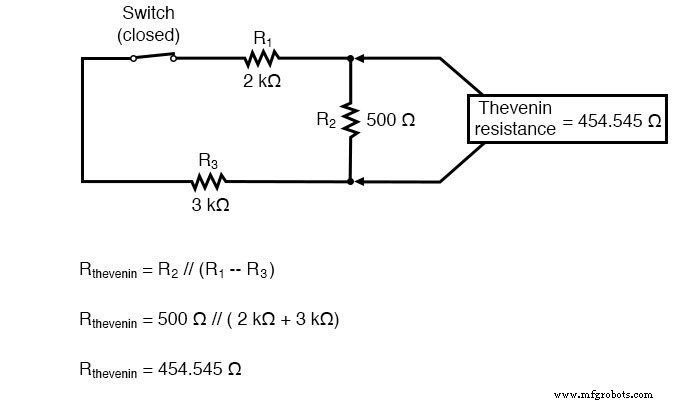
テブナンの等価物として回路を再描画すると、次のようになります。
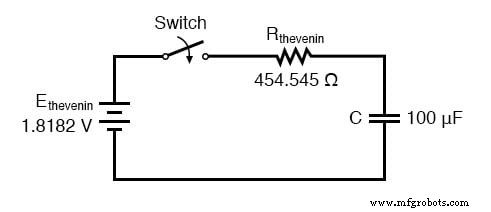
この回路の時定数は、テブナン抵抗に静電容量を掛けたものに等しくなります(τ=RC)。上記の値を使用して、次のように計算します。

これで、ユニバーサル時定数式を使用して、コンデンサ両端の電圧を直接解くことができます。 60ミリ秒の値を計算してみましょう。これは容量式であるため、電圧の計算を設定します。

繰り返しになりますが、コンデンサ電圧の開始値はゼロであると想定されているため、60ミリ秒でのコンデンサ両端の実際の電圧は、ゼロからの電圧変化量、つまり1.3325ボルトに等しくなります。
さらに一歩進んで、コンピューター分析を通じてテブナンRC回路と元の回路の同等性を実証することができます。これを実証するために、SPICE分析プログラムを使用します:
比較RC分析 *最初に、元の回路のネットリスト: v1 1 0 dc 20 r1 1 2 2k r2 2 3 500 r3 3 0 3k c1 2 3 100u ic =0 *次に、同等のテブナンのネットリスト: v2 4 0 dc 1.818182 r4 4 5 454.545 c2 5 0 100u ic =0 *現在、.005秒ごとにサンプリングして、一時的なものを分析しています *合計0.37秒の期間にわたって、 *元のコンデンサ両端の電圧の値 *回路(モード2と3の間)およびコンデンサの両端 *テブナン等価回路(ノード5と0の間) .tran .005 0.37 uic .print tran v(2,3)v(5,0) 。終わり
次のように出力されます:
時間 | v(2,3) | v(5) | 0.000E + 004.803E-064.803E-065.000E-031.890E-011.890E-011.000E-023.580E-013.580E-011.500E-025.082E-015.082E-012.000E-026.442E-016.442E-012.500E-027.689E -017.689E-013.000E-028.772E-018.772E-013.500E-029.747E-019.747E-014.000E-021.064E + 001.064E + 004.500E-021.142E + 001.142E + 005.000E-021.212E + 001.212E + 005.500 E-021.276E + 001.276E + 006.000E-021.333E + 001.333E + 006.500E-021.383E + 001.383E + 00 7.000E-021.429E + 001.429E + 007.500E-021.470E + 001.470E + 008.000E-021.505E + 001.505E + 008.500E-021.538E + 001.538E + 009.000E-021.568E + 001.568E + 009.500E-021.594E + 001.594E + 001.000E-011.617E + 001.617E + 001.050E-011.638E + 001.638E + 001.100 E-011.657E + 001.657E + 001.150E-011.674E + 001.674E + 001.200E-011.689E + 001.689E + 001.250E-011.702E + 001.702E + 001.300E-011.714E + 001.714E + 001.350E-011.725E + 001.725E + 001.400E-011.735E + 001.735E + 001.450E-011.744E + 001.744E + 001.500E-011.752E + 001.752E + 001.550E-011.758E + 001.758E + 001.600E-011.765E + 001.765E + 001.650E -011.770E + 001.770E + 001.700E-011.775E + 001.775E + 001.750E-011.780E + 001.780E + 001.800E-011.784E + 001.784E + 00 1.850E-011.787E + 001.787E + 001.900E-011.791E + 001.791E + 001.950E-011.793E + 001.793E + 002.000E-011.796E + 001.796E + 002.050E-011.798E + 001.798E + 002.100E-011.800E + 001.800E + 002.150E-011.802E + 001.802E + 002.200E-011.804E + 001.804E + 002.250E-011.805E + 001.805E + 002.300E-011.807E + 001.807E + 002.350E-011.808E + 001.808E + 002.400 E-011.809E + 001.809E + 002.450E-011.810E + 001.810E + 002.500E-011.811E + 001.811E + 002.550E-011.812E + 001.812E + 002.600E-011.812E + 001.812E + 002.650E-011.813E + 001.813E + 002.700E-011.813E + 001.813E + 002.750E-011.814E + 001.814E + 002.800E-011.814E + 001.814E + 002.850E-011.815E + 001.815E + 002.900E-011.815E + 001.815E + 002.950E -011.815E + 001.815E + 003.000E-011.816E + 001.816E + 003.050E-011.816E + 001.816E + 003.100E-011.816E + 001.816E + 003.150E-011.816E + 001.816E + 003.200E-011.817E + 001.817 E + 003.250E-011.817E + 001.817E + 003.300E-011.817E + 001.817E + 003.350E-011.817E + 001.817E + 003.400E-011.817E + 001.817E + 003.450E-011.817E + 001.817E + 003.500E- 011.817E + 001.817E + 003.500E-013.550E-013.550E-013.600E-011.818E + 001.818E + 003.650E-011.818E + 001.818E + 003 .700E-011.818E + 001.818E + 00
分析の途中のすべてのステップで、2つの回路(元の回路とテブナンの等価回路)のコンデンサは等しい電圧であるため、2つの回路が同等であることを示しています。
レビュー:
- 単純な直列よりも複雑なRCまたはL / R回路を分析するには、無効成分(コンデンサまたはインダクタ)を「負荷」として扱い、他のすべてを1の等価回路に減らすことにより、回路をテブナン等価回路に変換します。電圧源と1つの直列抵抗。次に、ユニバーサル時定数式を使用して、時間の経過とともに何が起こるかを分析します。
関連するワークシート:
- テブナン、ノートン、および最大電力伝達定理ワークシート










