並列抵抗-コンデンサ回路
直列の回路例で同じ値のコンポーネントを使用して、それらを並列に接続し、何が起こるかを確認します。
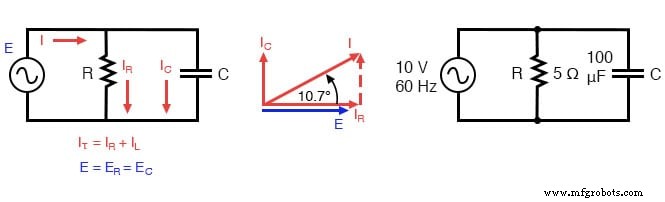
並列R-C回路。
並列の抵抗とコンデンサ
電源は直列の回路例と同じ周波数であり、抵抗とコンデンサは両方とも同じ値の抵抗と静電容量を持っているため、それらも同じ値のインピーダンスを持っている必要があります。したがって、同じ「指定された」値で分析テーブルを開始できます。
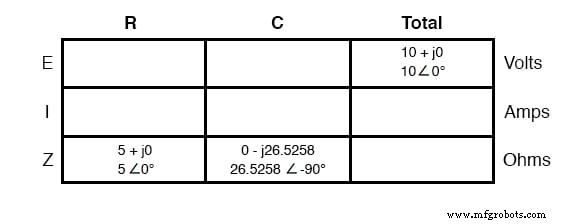
これは並列回路であるため、電圧はすべてのコンポーネントで均等に共有されることがわかっているため、すべての列に合計電圧(10ボルト∠0°)の数値を配置できます。
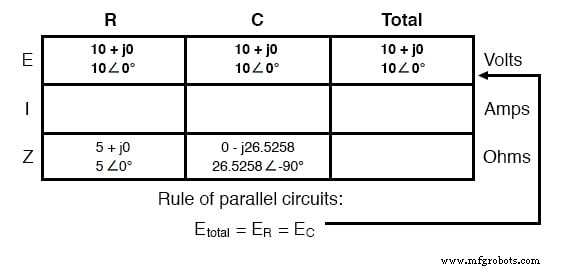
オームの法則を使用した計算
これで、オームの法則(I =E / Z)をテーブルの2つの列に垂直に適用して、抵抗を流れる電流とコンデンサを流れる電流を計算できます。
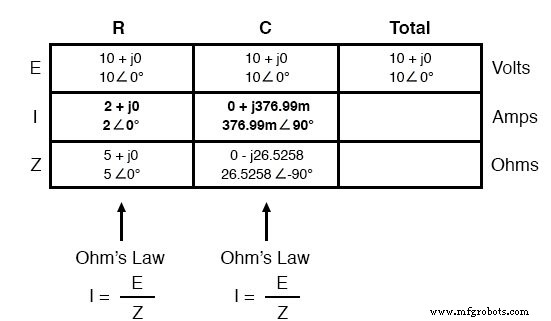
DC回路の場合と同様に、並列AC回路の分岐電流が合計されて合計電流が形成されます(キルヒホッフの電流法則):
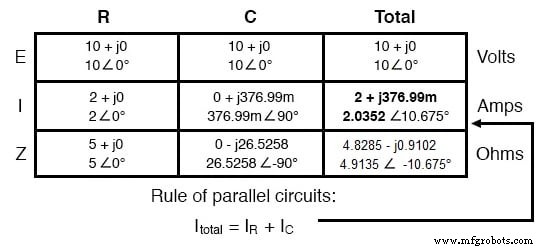
最後に、「合計」列で垂直方向にオームの法則(Z =E / I)を使用して、合計インピーダンスを計算できます。 ACインダクタンスの章で見たように、並列インピーダンスは、並列抵抗の計算に使用されるものと同じ逆数の式を使用して計算することもできます。
この並列インピーダンスの規則は、並列に配置されたインピーダンスの種類に関係なく当てはまることに注意してください。
言い換えると、並列抵抗、並列インダクタ、並列コンデンサ、またはそれらの組み合わせで構成される回路を計算するかどうかは関係ありません。インピーダンス(Z)の形式では、すべての用語が共通であり、適用できます。同じ式に均一に。
繰り返しますが、並列インピーダンスの式は次のようになります。
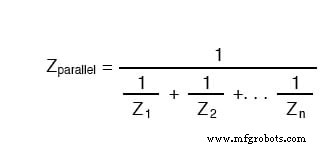
この方程式を使用することの唯一の欠点は、特に複雑な量を操作できる計算機の助けを借りずに、それを計算するために必要なかなりの量の作業です。並列回路の総インピーダンスの計算方法(オームの法則または逆数の式)に関係なく、同じ数値に到達します。
レビュー:
- インピーダンス(Z)は、並列回路解析の抵抗(R)と同じように管理されます。並列インピーダンスは、逆数の式を使用して減少し、合計インピーダンスを形成します。すべての計算は、必ず複雑な(スカラーではない)形式で実行してください。 ZTotal =1 /(1 / Z1 + 1 / Z2 +。。。1 / Zn)
- AC回路のオームの法則:E =IZ; I =E / Z; Z =E / I
- 抵抗とコンデンサが並列回路で混合されている場合(直列回路の場合と同様)、合計インピーダンスの位相角は0°から-90°の間のどこかになります。回路電流の位相角は0°から+ 90°の間です。
- 並列AC回路は、並列DC回路と同じ基本特性を示します。電圧は回路全体で均一であり、分岐電流が加算されて総電流を形成し、インピーダンスが減少して(逆数式により)総インピーダンスを形成します。 >
関連するワークシート:
- 直列および並列AC回路ワークシート
産業技術



