直列抵抗-コンデンサ回路

前のセクションでは、単純な抵抗のみおよびコンデンサのみのAC回路で何が起こるかを学びました。次に、2つのコンポーネントを直列に組み合わせて、効果を調査します。

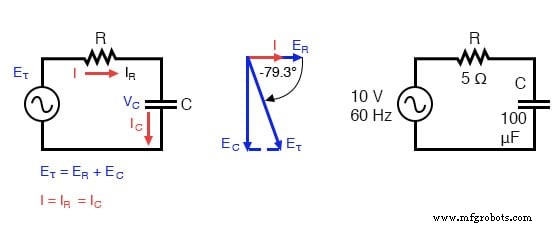
直列コンデンサ回路：電圧は電流を0°から90°遅らせます。

インピーダンス計算

抵抗は周波数に関係なくAC電流に対して5Ωの抵抗を提供し、コンデンサは60HzでAC電流に対して26.5258Ωのリアクタンスを提供します。

抵抗器の抵抗は実数（5Ω∠0°、または5 +j0Ω）であり、コンデンサのリアクタンスは虚数（26.5258Ω∠-90°、または0-j26.5258Ω）であるため、複合効果2つの成分のうち、2つの数値の複素数の合計に等しい電流に対する反対になります。

現在に対するこの複雑な反対の用語は、インピーダンスです。 、その記号はZであり、抵抗やリアクタンスと同様に、オームの単位でも表されます。上記の例では、合計回路インピーダンスは次のとおりです。

インピーダンスは、オームの法則の抵抗と同じように、予想どおりに電圧と電流に関連しています。

実際、インピーダンスが単純な抵抗よりもはるかに包括的な電子の流れに対する反対の表現であるように、これはDCエレクトロニクス（E =IR）で教えられたものよりもはるかに包括的なオームの法則です。任意の抵抗とリアクタンスは、個別にまたは組み合わせて（直列/並列）、単一のインピーダンスとして表すことができ、表す必要があります。

現在の計算

上記の回路の電流を計算するには、最初に電圧源の位相角基準を与える必要があります。これは一般にゼロと見なされます。 （抵抗性インピーダンスと容量性インピーダンスの位相角は常に 電圧または電流の特定の位相角に関係なく、それぞれ0°および-90°。）

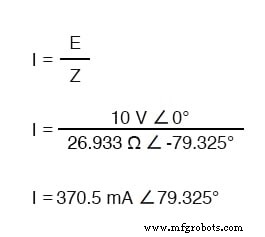
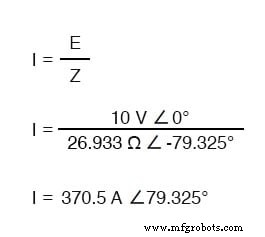
純粋な容量性回路と同様に、電流波は（ソースの）電圧波をリードしていますが、今回の差は完全な90°ではなく79.325°です。

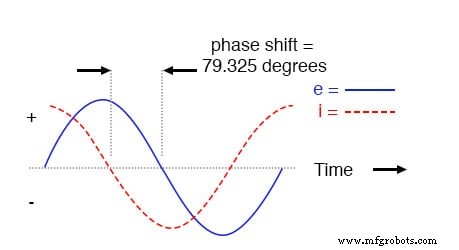
直列R-C回路の電圧は電流（電流リード電圧）より遅れます。

テーブルメソッド

ACインダクタンスの章で学んだように、回路量を整理する「テーブル」方式は、DC分析の場合と同様に、AC分析にも非常に便利なツールです。この直列回路の既知の数値を表にまとめ、このツールを使用して分析を続けましょう。

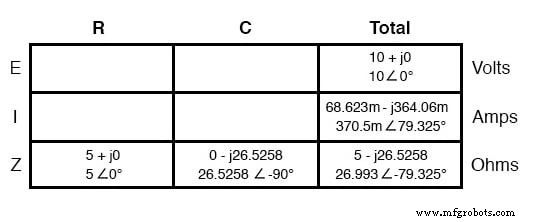
直列回路の電流はすべてのコンポーネントで均等に共有されるため、電流の「合計」列に配置された数値は、他のすべての列にも分配できます。

分析を続けると、オームの法則（E =IR）を垂直に適用して、抵抗とコンデンサの両端の電圧を決定できます。

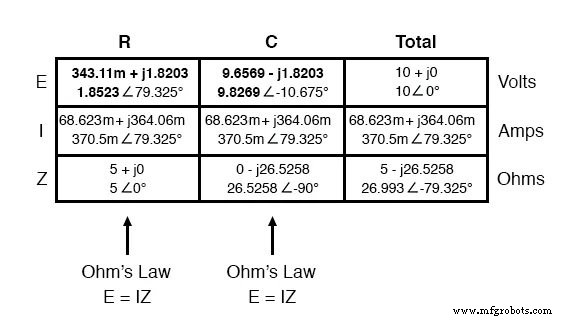
抵抗器の両端の電圧が、抵抗器を流れる電流とまったく同じ位相角を持っていることに注目してください。これは、EとIが同相であることを示しています（抵抗器の場合のみ）。コンデンサの両端の電圧の位相角は-10.675°で、正確に90°少ない 回路電流の位相角よりも。これは、コンデンサの電圧と電流がまだ互いに90°位相がずれていることを示しています。

SPICEを使用した計算

SPICEで計算を確認しましょう：

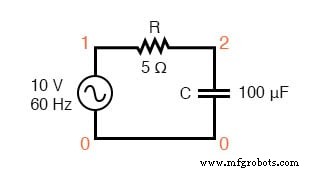
スパイス回路：R-C。

 acr-c回路 v1 1 0 ac 10 sin r1 1 2 5 c1 2 0 100u .ac lin 1 60 60 .print ac v（1,2）v（2,0）i（v1） .print ac vp（1,2）vp（2,0）ip（v1） 。終わり 周波数v（1,2）v（2）i（v1） 6.000E + 01 1.852E + 00 9.827E + 00 3.705E-01 freq vp（1,2）vp（2）ip（v1） 6.000E + 01 7.933E + 01 -1.067E + 01 -1.007E + 02 

繰り返しになりますが、SPICEは、現在の位相角を実際の位相角に180°を加えた値（またはマイナス180°）に等しい値で混乱させて印刷します。

ただし、この図を修正して、作業が正しいかどうかを確認するのは簡単なことです。この場合、現在の位相角に対してSPICEによって出力される-100.7°は正の79.3°に相当します。これは、以前に計算された79.325°の数値に対応します。

繰り返しになりますが、実際の電圧と電流の測定値に対応する計算された数値は、極の数値であることを強調する必要があります。 長方形ではなく形です！

たとえば、この直列抵抗-コンデンサ回路を実際に構築し、抵抗の両端の電圧を測定する場合、電圧計は 1.8523 を示します。 343.11ミリボルト（実際の長方形）または1.8203ボルト（想像上の長方形）ではなく、ボルト。

実際の回路に接続された実際の機器は、計算された数値のベクトルの長さ（大きさ）に対応する指標を提供します。複素数表記の長方形形式は、加算と減算を実行するのに役立ちますが、それだけで真の測定値に直接対応する極よりも抽象的な形式の表記です。

直列R-C回路のインピーダンス（Z）は、抵抗（R）と容量性リアクタンス（X _C ）が与えられた場合に計算できます。 ）。 E =IRなので、E =IX _C 、およびE =IZ、抵抗、リアクタンス、およびインピーダンスは、それぞれ電圧に比例します。したがって、電圧フェーザ図は、同様のインピーダンス図に置き換えることができます。

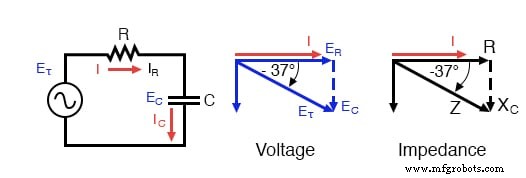
シリーズ：R-C回路のインピーダンスフェーザ図。

例： 与えられたもの：88.42マイクロファラッドコンデンサと直列の40Ω抵抗。 60ヘルツでのインピーダンスを求めます。

 XC =1 /（2πfC） XC =1 /（2π・60・88.42×10-6） XC =30Ω Z =R-jXC Z =40-j30 | Z | =sqrt（402 +（-30）2）=50Ω ∠Z=アークタンジェント（-30/40）=-36.87° Z =40-j30 =50∠-36.87° 

レビュー：

• インピーダンス は電流に対する反対の合計であり、（「実数」）抵抗と（「虚数」）リアクタンスの複素数（ベクトル）の合計です。
• インピーダンス（Z）は、直列回路解析の抵抗（R）と同じように管理されます。直列インピーダンスが加算されて、合計インピーダンスが形成されます。すべての計算は、必ず複雑な（スカラーではない）形式で実行してください。 Z _Total1 + Z ₂ +。 。 。 Z _n
• インピーダンスを構成するコンポーネントのタイプに関係なく、インピーダンスは常に直列に追加されることに注意してください。つまり、抵抗性インピーダンス、誘導性インピーダンス、および容量性インピーダンスは、数学的に同じように扱われます。
• 純粋な抵抗性インピーダンスの位相角は常に正確に0°です（Z _R =RΩ∠0°）。
• 純粋な容量性インピーダンスは、常に正確に-90°の位相角を持ちます（Z _C =X _C Ω∠-90°）。
• AC回路のオームの法則：E =IZ; I =E / Z; Z =E / I
• 回路内で抵抗とコンデンサが混在している場合、合計インピーダンスの位相角は0°〜-90°の範囲になります。

関連するワークシート：

• 直列および並列AC回路ワークシート