単純な並列（タンク回路）共振

タンク回路の共振

コンデンサとインダクタのリアクタンスが互いに等しい場合、タンク回路で共振状態が発生します。誘導性リアクタンスは周波数の増加とともに増加し、容量性リアクタンスは周波数の増加とともに減少するため、これら2つのリアクタンスが等しくなる周波数は1つだけになります。例：

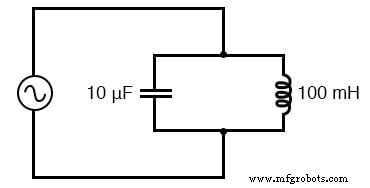
単純な並列共振回路（タンク回路）。

上記の回路には、10 µFのコンデンサと100mHのインダクタがあります。与えられた周波数でそれぞれのリアクタンスを決定するための方程式がわかっていて、2つのリアクタンスが互いに等しい点を探しているので、2つのリアクタンスの式を互いに等しく設定し、代数的に周波数を解くことができます。 ：

これで、ヘンリーのインダクタンス（L）とファラッドの静電容量（C）の値が与えられた場合の、タンク回路の共振周波数を示す式が得られました。この例の回路にLとCの値を接続すると、159.155Hzの共振周波数に到達します。

個々のインピーダンスの計算

共鳴で何が起こるかは非常に興味深いものです。容量性リアクタンスと誘導性リアクタンスが互いに等しい場合、合計インピーダンスは無限大に増加します。つまり、タンク回路はAC電源から電流を引き込みません！

10 µFのコンデンサと100 mHのインダクタの個々のインピーダンスを計算し、並列インピーダンスの式を調べて、これを数学的に示すことができます。

ご想像のとおり、これらのコンポーネント値を選択して、操作しやすい共振インピーダンスを実現しました（100Ωでも）。

並列インピーダンス式

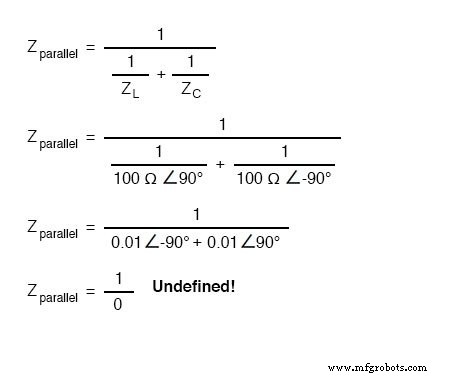
ここで、並列インピーダンスの式を使用して、合計Zがどうなるかを確認します。

SPICEシミュレーションプロット

数値をゼロで割って意味のある結果を得ることができませんが、結果は無限大の値に近づいていると言えます。 2つの並列インピーダンスが互いに近づくにつれて。

これが実際に意味することは、タンク回路の総インピーダンスが無限大であるということです（開回路として動作します） ）共振時。短いSPICEシミュレーションで、広い電源周波数範囲にわたってこの結果をプロットできます。

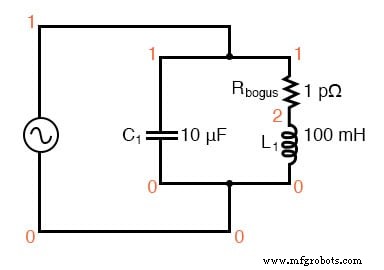
SPICEシミュレーションに適した共振回路。

1ピコオーム（1pΩ）の抵抗は、SPICEの制限、つまり、直接インダクター電圧源ループを含む回路を分析できないという制限を克服するために、このSPICE分析に配置されます。 （下の図）回路の動作への影響を最小限に抑えるために、非常に低い抵抗値が選択されました。

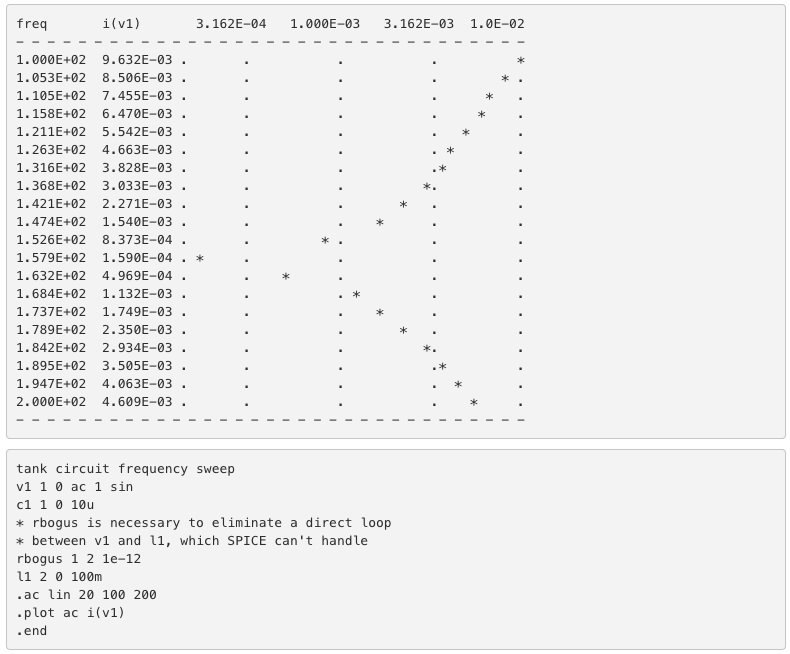
このSPICEシミュレーションは、100〜200 Hzの周波数範囲にわたる回路電流を20の偶数ステップ（100および200 Hzを含む）でプロットします。グラフの現在の大きさは左から右に増加し、周波数は上から下に増加します。

この回路の電流は、157.9 Hzの分析ポイントの周りで急激に低下します。これは、159.155Hzの予測共振周波数に最も近い分析ポイントです。この時点で、電源からの合計電流はゼロになります。

「ナツメグ」のグラフィカルなポストプロセッサプロット

上記のプロットは、上記のスパイス回路ファイル（* .cir）から作成され、最後の行のコマンド（.plot）は、任意のプリンターまたは端末でテキストプロットを作成します。見栄えの良いプロットは、スパイスパッケージの一部である「ナツメグ」グラフィカルポストプロセッサによって生成されます。

上記のスパイス（* .cir）は、害はありませんが、plot（.plot）コマンドを必要としません。次のコマンドは、以下のプロットを生成します。

スパイス-b-r共鳴.raw共鳴.cir （-bバッチモード、-r rawファイル、入力はresonant.cir） ナツメグレゾナント.raw 

ナツメグプロンプトから：

> setplot ac1（プロットのリストについてはsetplot {enter}）>表示（信号のリスト用）> plot mag（v1＃branch） （複素電流ベクトルv1＃branchの大きさ） 

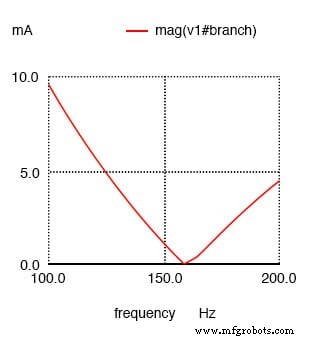
Nutmegは、並列共振回路の電流I（v1）のプロットを生成します。

ボード線図

ちなみに、このSPICEコンピューター分析によって生成されたグラフ出力は、より一般的にはボード線図として知られています。 。このようなグラフは、一方の軸に振幅または位相シフトをプロットし、もう一方の軸に周波数をプロットします。ボード線図曲線の急峻さは、回路の「周波数応答」、つまり周波数の変化に対する回路の感度を特徴づけます。

レビュー：

• 共振は、容量性リアクタンスと誘導性リアクタンスが互いに等しい場合に発生します。
• 抵抗（R）のないタンク回路の場合、共振周波数は次の式で計算できます

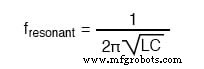
• 電源周波数が共振に近づくと、並列LC回路の総インピーダンスは無限大に近づきます。
• ボード線図 は、一方の軸に波形の振幅または位相を、もう一方の軸に周波数をプロットしたグラフです。

関連するワークシート：

• 無線通信ワークシートの基礎
• レゾナンスワークシート