シンプルシリーズレゾナンス

同様の効果は、直列の誘導/容量性回路でも発生します。共振状態に達すると（容量性リアクタンスと誘導性リアクタンスが等しい）、2つのインピーダンスが互いに打ち消し合い、合計インピーダンスがゼロになります。 例：

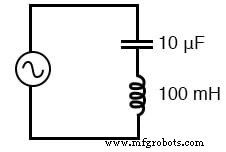
単純な直列共振回路。

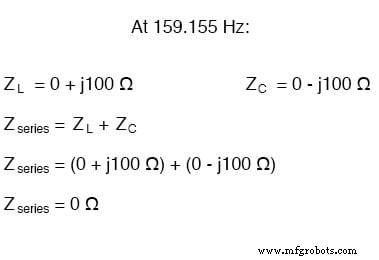
159.155 Hzの共振周波数で合計直列インピーダンスが0Ωに等しい場合、結果は短絡になります。 共振時にAC電源の両端。上に描いた回路では、これは良くありません。

コンデンサとインダクタに直列に小さな抵抗（下の図）を追加して、最大回路電流をいくらか制限し、同じ周波数範囲で別のSPICE分析を実行します。

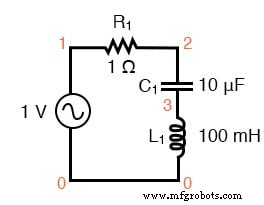
SPICEに適した直列共振回路。

シリーズLC回路 v1 1 0 ac 1 sin r1 1 2 1 c1 2 3 10u l1 3 0100m .ac lin 20100200 .plot ac i（v1） 。終わり 

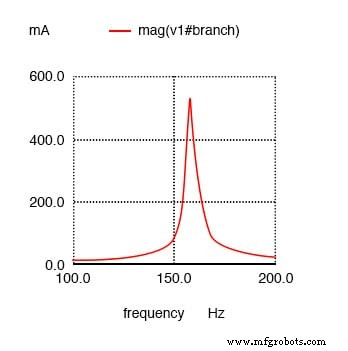
電流I（v1）の直列共振回路プロット。

前と同じように、回路電流の振幅は下から上に向かって増加し、周波数は左から右に向かって増加します。ピークは、プロットされた周波数ポイント157.9 Hzにあるように見えます。これは、予測される共振ポイント159.155Hzに最も近い分析ポイントです。

これは、私たちの共振周波数の式が、単純な並列LC回路の場合と同様に、単純な直列LC回路にも当てはまることを示唆しています。

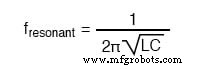
注意点は、直列LC共振回路の場合です。共振時に直列LC回路に存在する可能性のある大電流のため、各コンポーネントが持つため、コンデンサとインダクタの間に危険な高電圧降下が発生する可能性があります。大きなインピーダンス。

上記の例のSPICEネットリストを編集して、コンデンサとインダクタの両端の電圧のプロットを含めて、何が起こるかを示すことができます。

シリーズLC回路 v1 1 0 ac 1 sin r1 1 2 1 c1 2 3 10u l1 3 0100m .ac lin 20100200 .plot ac i（v1）v（2,3）v（3） 。終わり 

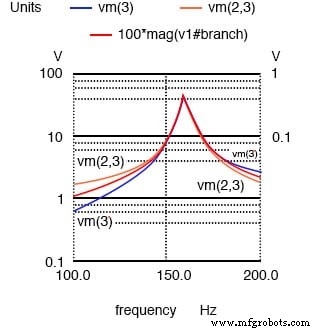
Vc =V（2,3）70 Vピーク、VL =v（3）70 Vピーク、I =I（V1＃branch）0.532Aピークのプロット。

SPICEによると、コンデンサとインダクタの両端の電圧は、約70ボルトのどこかでピークに達します！

これは、1ボルトしか生成しない電源装置としては非常に印象的です。言うまでもなく、このような回路を実験するときは注意が必要です。 AC解析ステートメント（.ac lin 20 100 200）のステップ数が少ないため、SPICE電圧が期待値よりも低くなっています。期待値はいくらですか？

与えられた：fr =159.155 Hz、L =100mH、R =1 XL =2πfL=2π（159.155）（100mH）=j100Ω XC =1 /（2πfC）=1 /（2π（159.155）（10µF））=-j100Ω Z =1 + j100 -j100 =1Ω I =V / Z =（1 V）/（1Ω）=1 A VL =IZ =（1 A）（j100）=j100 V VC =IZ =（1 A）（-j100）=-j100 V VR =IR =（1 A）（1）=1 V Vtotal =VL + VC + VR Vtotal =j100 -j100 +1 =1 V 

コンデンサとインダクタの電圧の期待値は100Vです。この電圧は、これらのコンポーネントにそのレベルまでストレスを与えるため、それに応じて定格を設定する必要があります。ただし、これらの電圧は位相がずれてキャンセルされ、印加電圧である1Vのみの3つのコンポーネントすべてに合計電圧が発生します。印加電圧に対するコンデンサ（またはインダクタ）電圧の比率が「Q」係数です。

 Q =VL / VR =VC / VR 

レビュー：

• 電源周波数が共振に近づくと、直列LC回路の総インピーダンスはゼロに近づきます。
• 単純なタンク回路の共振周波数を決定するための同じ式は、単純な直列回路にも適用されます。
• 大電流が流れ、個々のコンポーネントのインピーダンスが大きいため、共振時に直列LC回路の個々のコンポーネント間に非常に高い電圧が形成される可能性があります。

関連するワークシート：

• 直列および並列AC回路ワークシート