スペクトル分析の詳細
特に FFT の形式でのコンピューター化されたフーリエ解析 アルゴリズムは、波形とそれに関連するスペクトル成分の理解を深めるための強力なツールです。
.fourierオプションとしてSPICEシミュレータにプログラムされたこの同じ数学的ルーチンは、測定された信号に対してリアルタイムのフーリエ解析を実行するために、さまざまな電子テスト機器にもプログラムされています。
このセクションでは、このようなツールの使用といくつかの異なる波形の分析について説明します。
まず、523.25Hzの周波数の単純な正弦波があります。この特定の周波数値は、ピアノキーボードの「C」ピッチであり、「中央のC」の1オクターブ上にあります。
実際、このデモンストレーションで測定された信号は、完全な正弦波に似ていると私が見つけた最も近い楽器の「声」であるパンフルートの音色を生成するように設定された電子キーボードによって作成されました。以下のプロットは、オシロスコープのディスプレイから取得したもので、時間の経過に伴う信号の振幅(電圧)を示しています。
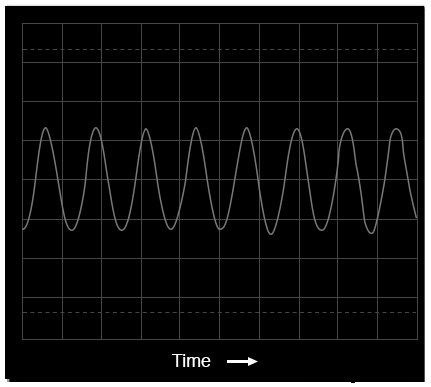
オシロスコープの表示:電圧と時間
オシロスコープで見ると、正弦波は画面上で水平にトレースされた波状の曲線のように見えます。このオシロスコープのディスプレイの横軸には、「時間」という文字と、時間の進行方向を指す矢印が付いています。もちろん、曲線自体は、時間の経過に伴う電圧の周期的な増加と減少を表しています。
よく観察すると、正弦波の形に欠陥があることがわかります。残念ながら、これは波形の分析に使用された特定の機器の結果です。テスト機器の癖によるこのような特性は、技術的にはアーティファクトとして知られています。 :実験を行うために使用された機器の特殊性のためだけに存在する現象。
これと同じAC電圧をスペクトラムアナライザで見ると、結果はまったく異なります。
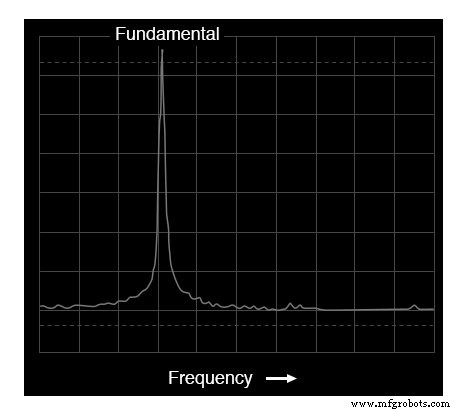
スペクトラムアナライザの表示:電圧と周波数
ご覧のとおり、ディスプレイの横軸には「周波数」という文字が付いており、この測定の領域を示しています。曲線上の単一のピークは、ディスプレイの幅でカバーされる周波数の範囲内での単一の周波数の優位性を表しています。
このアナライザー機器の目盛りに数字が付いている場合、このピークは523.25Hzで発生していることがわかります。ピークの高さは信号の振幅(電圧)を表します。
電子キーボード(C-E-G、ハ長調コード)で3つの異なる正弦波トーンを混ぜ合わせて結果を測定すると、オシロスコープのディスプレイとスペクトラムアナライザのディスプレイの両方がこの複雑さの増大を反映しています。
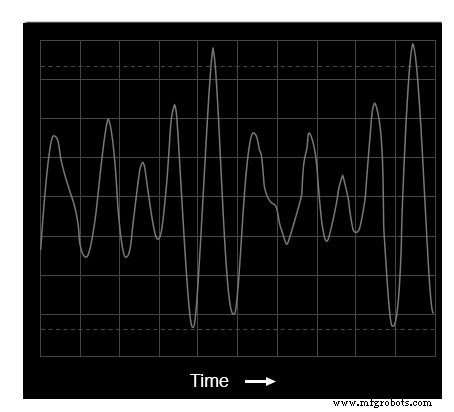
Oscilloscapeディスプレイ:3つのトーン
オシロスコープの表示(時間領域)には、以前よりもはるかに多くの山と谷がある波形が表示されます。これは、これら3つの周波数の混合の直接的な結果です。お気づきのように、これらのピークのいくつかは元のシングルピッチ波形のピークよりも高く、他のピークは低くなっています。
これは、3つの異なる波形が、それぞれの位相シフトが時間とともに変化するにつれて、互いに補強と打ち消しを交互に繰り返す結果です。
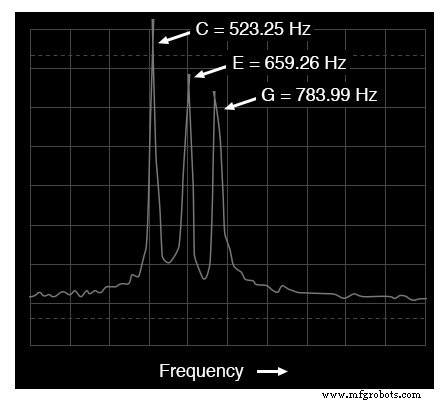
スペクトラムアナライザの表示:3つのトーン
スペクトル表示(周波数領域)の解釈ははるかに簡単です。各ピッチは、曲線上の独自のピークで表されます。これらの3つのピーク間の高さの違いは、テスト機器のもう1つのアーティファクトです。これらの波形の生成と分析に使用される機器内の制限の結果であり、音楽コード自体の必要な特性ではありません。
前に述べたように、これらの波形を生成するために使用されるデバイスは、電子キーボードです。これは、さまざまな楽器の音色を模倣するように設計された楽器です。
パンフルートの「音声」は、純粋な正弦波(スペクトラムアナライザディスプレイの単一周波数)に最もよく似ているため、最初のデモンストレーションで選択されました。しかし、他の楽器の「声」はこれほど単純ではありません。実際、 any によって生成される独特のトーン 楽器はその波形(または周波数のスペクトル)の関数です。
たとえば、トランペットトーンの信号を見てみましょう。
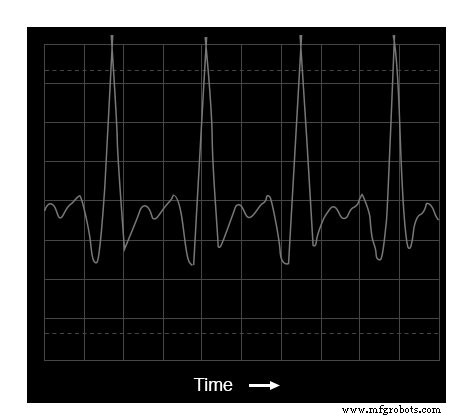
オシロスコープの表示:トランペットトーンの波形
このトーンの基本周波数は、最初のパンフルートの例と同じです。523.25Hz、「ミドルC」の1オクターブ上です。
波形自体は、純粋で単純な正弦波形式とはほど遠いものです。繰り返される非正弦波形は、さまざまな振幅と周波数の一連の正弦波形と同等であることがわかっているので、スペクトラムアナライザのディスプレイに複数のピークが表示されることを期待する必要があります。
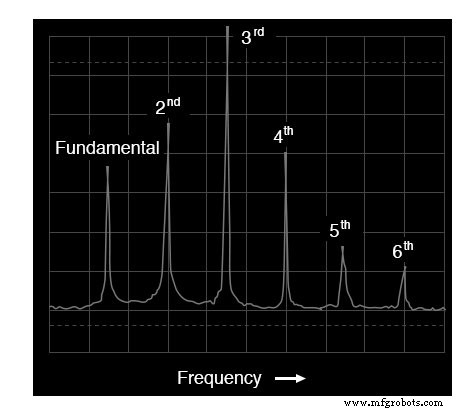
トランペットトーンのスペクトル
確かにそうです! 523.25 Hzの基本周波数成分は左端のピークで表され、連続する各高調波はアナライザー画面の幅に沿った独自のピークとして表されます。
2次高調波は基本波の2倍の周波数(1046.5 Hz)であり、3次高調波は基本波の3倍の周波数(1569.75 Hz)であり、以下同様です。このディスプレイには最初の6つの倍音のみが表示されますが、この複雑なトーンを構成するものは他にもたくさんあります。
キーボードで別の楽器の声(アコーディオン)を試してみると、同様に複雑なオシロスコープ(時間領域)のプロットとスペクトラムアナライザー(周波数領域)の表示が得られます。
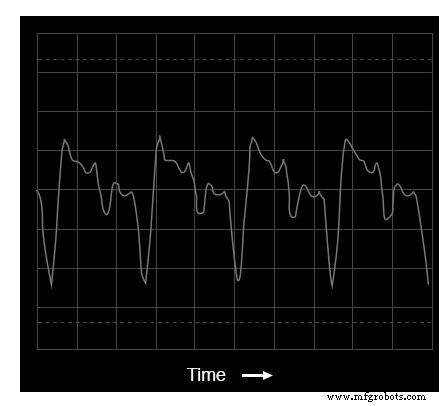
オシロスコープの表示:アコーディオントーンの波形
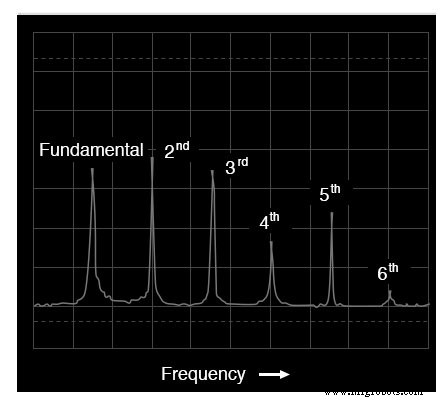
アコーディオントーンのスペクトル
トランペットとアコーディオンのスペクトル表示の相対的な高調波振幅(ピーク高さ)の違いに注意してください。両方の楽器の音色には、1次(基本)から6次(およびそれ以降)までのすべての倍音が含まれていますが、比率は同じではありません。
各楽器には、その音色に固有の倍音の「署名」があります。この複雑さはすべて、単一の音符に関連していることに注意してください。 これらの2つの楽器の「声」で遊んだ。たとえば、アコーディオンで複数の音を演奏すると、ここで見られるものよりもはるかに複雑な周波数の混合が作成されます。
オシロスコープとスペクトラムアナライザの分析能力により、実際の波形の例から波形とその高調波スペクトルに関する一般的な規則を導き出すことができます。純粋な正弦波からの逸脱は、さまざまな振幅と周波数の複数の正弦波波形の混合に相当することをすでに知っています。
ただし、注意深く観察することで、これよりも具体的にすることができます。たとえば、方形波に近い波形の時間および周波数領域のプロットに注意してください。
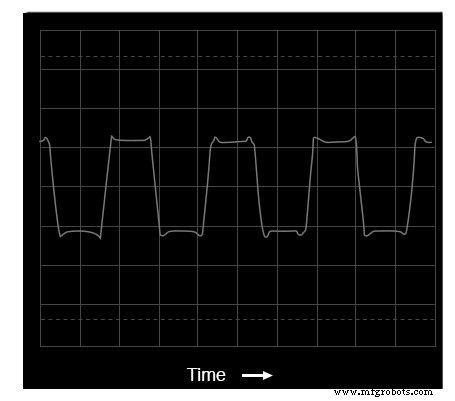
方形波のオシロスコープの時間領域表示
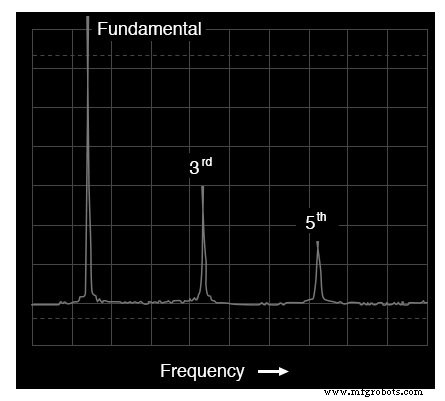
方形波のスペクトル(周波数領域)
スペクトル分析によると、この波形には no が含まれています 偶数次高調波、奇数のみ。このディスプレイには6次高調波を超える周波数は表示されませんが、振幅が下降する奇数次のみの高調波のパターンは無期限に続きます。
方形波は無限の奇数次高調波で構成されていることをSPICEですでに見たので、これは当然のことです。ただし、トランペットとアコーディオンの音には両方が含まれていました。 偶数次および奇数次の高調波。
この高調波成分の違いは注目に値します。三角波の分析を続けて調査を続けましょう:
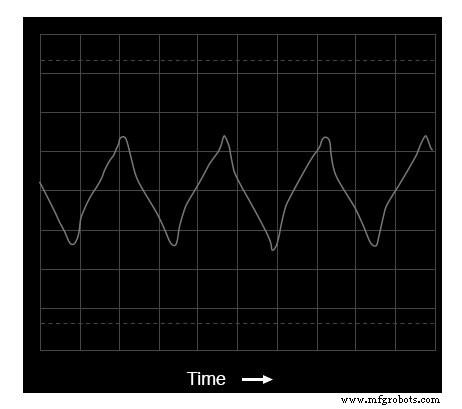
三角波のオシロスコープの時間領域表示
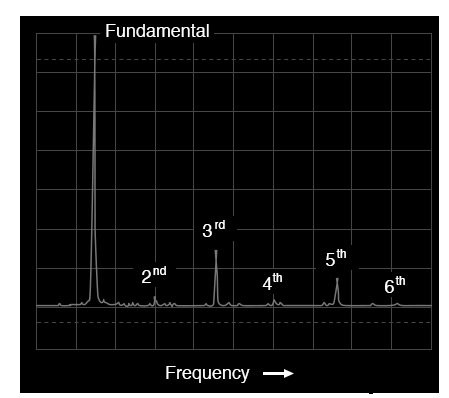
三角波のスペクトル
この波形には、実質的に偶数次の高調波はありません。(上の図)スペクトラムアナライザのディスプレイに表示される重要な周波数ピークは、基本周波数の奇数倍に属します。
2次、4次、6次の高調波に小さなピークが見られますが、これはこの特定の三角形の波形の欠陥によるものです(この場合も、この分析で使用したテスト機器のアーティファクトです)。
完全な正三角形の波形は、完全な方形波のように、高調波さえも生成しません。三角波の高調波スペクトルが方形波のスペクトルと同一ではないことは、検査から明らかです。それぞれの高調波ピークの高さは異なります。ただし、2つの異なる波形は、高調波がないという点で一般的です。
別の波形を調べてみましょう。これは三角波と非常によく似ていますが、立ち上がり時間が立ち下がり時間と同じではない点が異なります。 のこぎり波として知られています 、そのオシロスコープのプロットは、適切な名前が付けられていることを示しています:
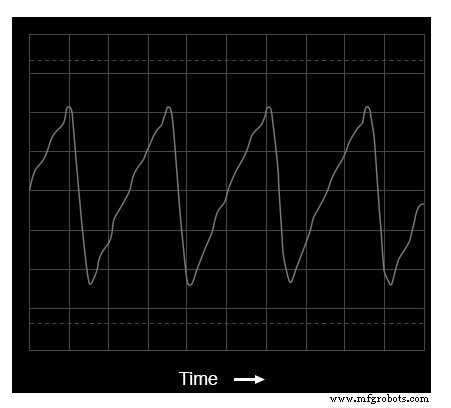
のこぎり波の時間領域表示
この波形のスペクトル分析をプロットすると、通常の三角波の結果とはまったく異なる結果が得られます。この分析では、偶数次の高調波(2番目と4番目)が強く存在することが示されています。
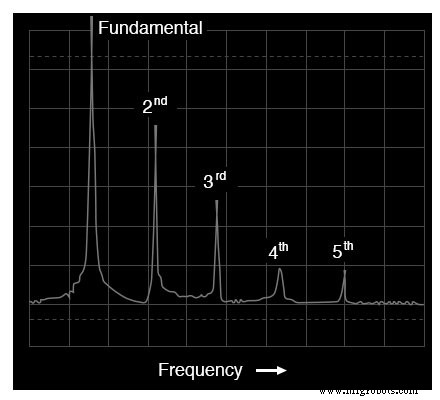
のこぎり波の周波数領域表示
偶数次高調波がある波形と偶数次高調波がない波形の違いは、三角形の波形とのこぎり波の違いにあります。
その違いは対称性です 波の水平中心線の上下。中心線の上下で対称な波形(両側の形状が互いに正確にミラーリングしている)には、 no が含まれます。 偶数次高調波。
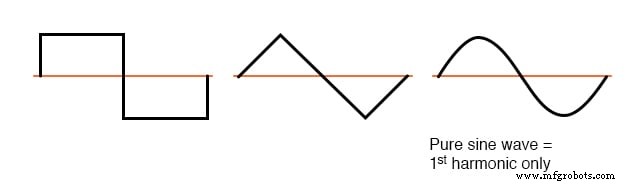
x軸の中心線に関して対称な波形には、奇数次の高調波のみが含まれます
方形波、三角波、および純粋な正弦波はすべてこの対称性を示し、すべてに高調波がありません。トランペットトーン、アコーディオントーン、のこぎり波などの波形は、中心線の周りで非対称であるため、 高調波も含まれています。
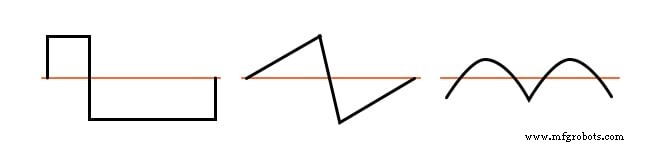
非対称波形には偶数次高調波が含まれています
この中心線の対称性の原則を、ゼロの周りの対称性と混同しないでください。 ライン。示されている例では、波形の水平中心線は時間領域グラフでたまたまゼロボルトですが、これは高調波成分とは関係ありません。
この高調波成分の規則(非対称波形のみの高調波でも)は、波形が「DC成分」でゼロボルトより上または下にシフトされているかどうかに関係なく適用されます。さらに明確にするために、DC電圧でシフトされた同じ波形のセットを示し、それらの高調波の内容は変更されていないことに注意してください。
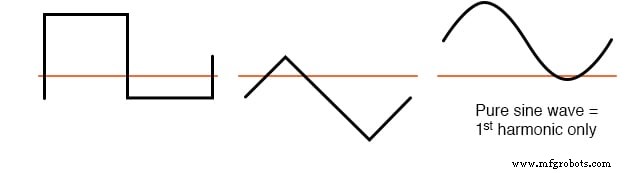
これらの波形は奇数次高調波のみで構成されています
繰り返しますが、波形に存在するDC電圧の量は、その波形の高調波周波数成分とは何の関係もありません。
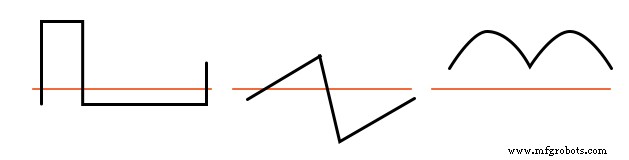
これらの波形には偶数次高調波が含まれています
この調和のとれた親指のルールが知っておくべき重要なルールであるのはなぜですか?これは、AC回路の高調波と特定の回路コンポーネントとの関係を理解するのに役立ちます。
AC電源回路の正弦波歪みのほとんどの原因は対称的である傾向があるため、これらのアプリケーションでは偶数次の高調波はめったに見られません。
これは、電力システムの設計者であり、高調波の低減を前もって計画している場合に知っておくとよいでしょう。高調波が実際には存在しない場合でも、奇数次の高調波周波数を軽減することだけを気にする必要があります。
また、スペクトラムアナライザまたは周波数計を使用してAC回路の高調波を測定する場合、その回路の何かが非対称でなければならないことを知っています。 正弦波の電圧または電流を歪めると、その手がかりが問題の原因を特定するのに役立つ場合があります(AC波形の半分のサイクルを他の半サイクルよりも歪める可能性が高いコンポーネントまたは条件を探します)。
非正弦波形の解釈をガイドするこのルールができたので、整流回路によって生成されるような波形には、中心の上下で対称性がまったくない、このような強い偶数次高調波が含まれている必要があります。
レビュー:
- 水平中心線の上下で対称な波形には、偶数次の高調波は含まれていません。
- 存在するDC「バイアス」電圧の量(波形の「DC成分」)は、その波の高調波周波数成分に影響を与えません。
関連するワークシート:
- 基本的なオシロスコープ操作ワークシート
- 受動積分器および微分回路のワークシート
産業技術



