求心力と遠心力の違い[説明]

この記事では、求心力と遠心力とは何ですか？ そしてそれらが実際の生活でどのように機能するか。その定義、動作、例、および求心力と遠心力の違い 写真で説明されています 。

さらに、PDFファイルをダウンロードすることもできます 最後にこの記事の。

求心力とは何ですか？

求心力は、オブジェクトが湾曲したパスをたどり、体が移動している中心に向けられる力として定義されます。または、簡単に言えば、求心力は、オブジェクトを円形のパスに沿って動かし続けるように作用する力です。

求心力の働き

ロープが円の周りを回転し、その端に缶が取り付けられていると想像してみてください。缶は、その円形の経路のために速度が絶えず変化しているため、一定の加速状態にあります。缶の加速は、物体に作用する正味の力によって引き起こされます。

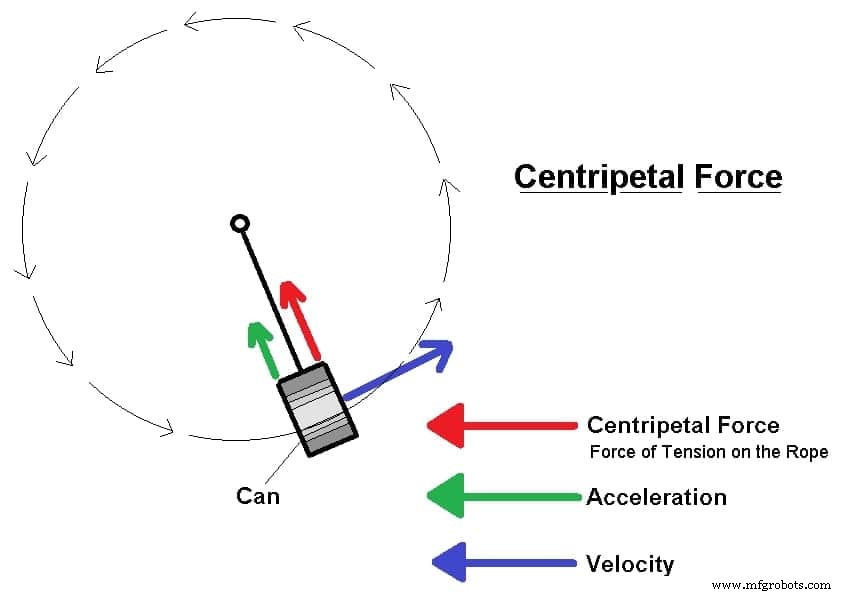
これにより、常にオブジェクトが円の中心に向かって引っ張られます。この力がないと、オブジェクトは直線運動を続けます。求心力はロープの張力です。

求心力は、質量速度の2乗を半径で割ったものに相当します。これらの変数が変化すると、求心力の質量または速度が増加するか、半径が減少すると、求心力が増加します。

質量または速度の減少または半径の増加は、求心力の減少をもたらします。ロープが切断されると、缶は円形の経路を維持できなくなり、ニュートンの最初の慣性の法則により、直線の接線で飛行します。

求心力の例

1. 重力によって月が地球の中心に向かって引っ張られます。この極は、月を地球の周りの軌道に維持する求心力です。地球の重力が存在しなくなった場合、月は直線で宇宙に飛んでいきます。
2. 求心力のもう1つの例は、タイヤが回転するときに泥をタイヤに結合する力です。タイヤの回転速度が上がると、求心力は泥をタイヤに保持するのに十分な大きさではなくなり、泥は直線のタンゲットでタイヤから飛び出します。

求心力の公式

求心力は通常、以下の式で計算されます。

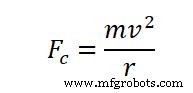
どこで、

• Fc=中心力
• m=オブジェクトの質量
• v=速度
• r=半径

遠心力とは何ですか？

これは、回転の中心から離れて円形のパスを移動するオブジェクトが受ける外部の想像上の力です。遠心力の理論は、遠心分離機、遠心ポンプ、遠心ガバナ、その他のデバイスなどの回転デバイスの物理を定義するために使用されます。

遠心力の働き

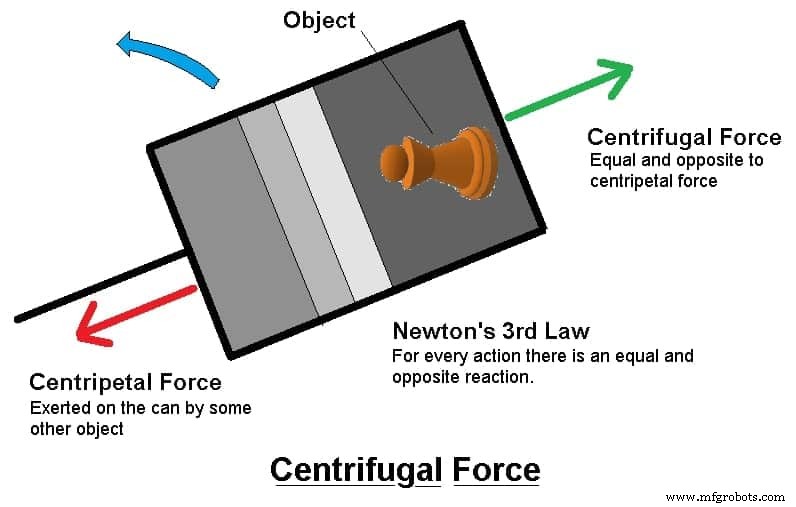
紐に取り付けられた缶で話し合ったように。求心力は、弦に張力をかける力です。この例には、缶の外側と缶の内側の2つの視点があります。

ニュートンの第3法則がすべての行動について述べているように、缶の外側からは等しく反対の反作用があり、求心力に対して外向きの反力があるはずです。この中心逃げ力は遠心力として知られています。

反力遠心力は求心力に対する反力です。湾曲した動きをする缶は、回転軸に向かって絶えず加速します。この求心加速度は、他の物体によって缶に加えられる求心力によって提供されます。

これは反作用遠心力であり、回転の中心から離れる方向に向けられ、求心加速度を生成するオブジェクトに回転缶によって加えられます。オブジェクトが缶の中に置かれている場合、オブジェクトには、缶の底に向かって回転の中心から離れるように押す外向きの力があるように見えます。

見かけの遠心力

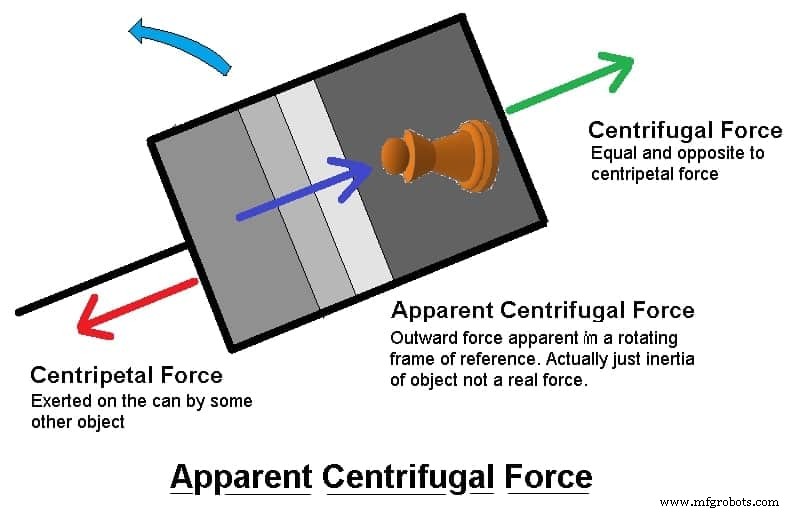
見かけの遠心力は、最も一般的には、回転座標系で見られる外向きの力として導入されます。それは相互作用の一部ではなく、実際にはオブジェクトの慣性であるという意味で、明白または想像上のものです。オブジェクトは自然に直線で移動したいのですが、求心力ではそれができません。

このタイプの力は、非慣性座標系での運動の記述に関連付けられており、架空の力または慣性力と呼ばれます。反動および見かけの遠心力は実際の力ではありません。したがって、それは力ではなく、回転の結果です。

見かけの遠心力は、実際には物体の慣性です。遠心力のより正確な定義は、遠心力の欠如です。

遠心力の例

1. 極と赤道での物体の重量。
2. 曲がるときに車両が滑り落ちるか、カーブを走行中にスリップします。

遠心力の計算式

遠心力は通常、以下の式で計算されます。オブジェクトの速度がわかっていると考えてください。これは、

によって計算されます。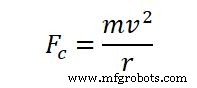

どこ

• V=移動する缶の速度
• r=移動する缶の中心からの距離です
• m=移動する缶の質量

角速度がわかっていて、それが次のように計算される場合

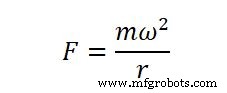
どこ

• ω=角速度
• r=移動缶の中心からの距離
• m=移動する缶の質量

求心力と遠心力の違い

求心力と遠心力の主な違いは次のとおりです。

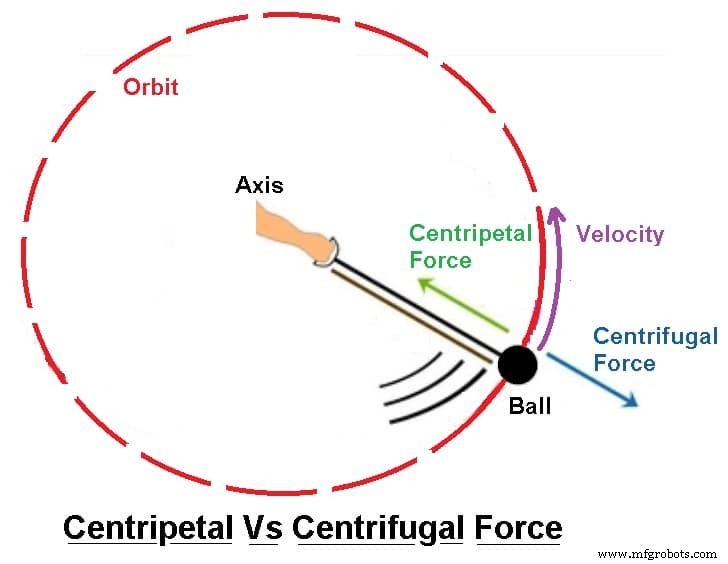
比較に基づく	求心力	遠心力
定義	これは、オブジェクトを円形のパス上で動かし続けるように作用し、円の中心に向けられる力として定義されます。	力は、回転の中心から離れて円形の経路を移動するオブジェクトが受ける外部の想像上の力として定義されます。
簡単な言葉で	求心力は円運動に必要な力です。	遠心力とは、物体を中心から逃がす力です。
自然	それは実際の力を考慮し、実際の生活に影響を及ぼします。	これは架空の力と見なされますが、実際の効果もあります。
動きの方向	方向が中心に向かって回転します。	方向を変えずに直進します。
観察	これは慣性座標系から見たものです。	これは非慣性座標系から見たものです。
式	F=遠心力と反対方向のmv²/r。	F =m v 求心力と反対方向に²/r。
例	地球の周りを周回する月。	方向転換中に車両が滑り落ちます。
アプリケーション	ジェットコースターでは、求心力の助けを借りて端に沿って鋭角に曲がり、トラックから離れるのを防ぎます。	遠心力がライダーに空中で感じさせることでライダーに喜びを与えるグラビトロンの乗り心地を見たことがあるはずです。

まとめ

上で説明したように、求心力は、オブジェクトを円で動かすために必要な力です。一方、遠心力は、回転座標系で見たときにすべてのオブジェクトに作用するように見える慣性力です。

---

ですから、今のところ、「求心力と遠心力」について学んだことを願っています。 「。この記事について質問や疑問がある場合は、コメントでお気軽にお問い合わせください。この記事が役に立ったら、お友達と共有してください。

受信トレイに無料のPDFが必要ですか？次に、ニュースレターを購読します。