トラッピングシステムにおける準単一分子とプラズモン空洞の間の強力な結合

はじめに

近年、光双極子トラップを使用して原子または分子をトラップおよび冷却することは、ボーズ・アインシュタイン凝縮を達成し、基本的な物理法則をテストし、基本的な物理定数をより正確に測定するための有望な技術です[1–3]。光双極子トラップは、主に入射光の勾配力を使用して、原子に双極子効果を生成します。赤で離調したトラップの場合、原子は引力ポテンシャルの下で光強度が最も強い位置にトラップされます[4]。レイリー散乱とラマン散乱により、トラップされた原子は見かけの原子コヒーレンスと加熱効果を受けます。同時に、最も強い光の位置では、核エネルギーレベルは深刻な光周波数シフトを持っています[1]。逆に、青色で離調したトラップ[5、6]の場合、原子は排除ポテンシャル[6–8]の下で最も弱い光強度の領域にトラップされます。赤で離調したトラップと比較して、弱い入射光で光子の散乱率を大幅に下げることができるため、小さな粒子をより安定してトラップすることができます。ただし、青色にデチューンされたトラップの構築は複雑であることがよくあります[9、10]。表面プラズモンポラリトン（SPP）は、誘電体と金属の間の界面に閉じ込められた自由電子振動に結合した光波のハイブリッドモードであり、THzデバイスの分野での幅広いアプリケーションに大きな可能性を秘めています[11–14]。材料[15]、センサー[16]、メタ表面[17]、および量子情報処理[18]。光トラッピングとプラズモン構造を組み合わせることで、統合された光学部品を開発することができます。たとえば、Chang etal。孤立した原子トラップのためにナノチップとマイクロディスクキャビティを組み合わせたナノ構造を使用することを提案しました[19]。 Chen etal。プラズモンナノホールのアレイで青色離調光に基づく安定した3D原子トラッピングを実現しました[20]。サブ波長の穴の配列を持つ周期的なプラズモンナノ構造は、興味深い光学特性を持っています。これは、原子や分子などの小さな粒子をトラップするための有望なシナリオです。

プラズモニックキャビティと分子間の強い結合は、量子電磁力学現象の基礎研究に関心を集めるだけでなく、量子情報処理においても明るい展望を持っています[21–23]。光と物質の相互作用の強さを大幅に高めることができるプラズモン空洞は、室温で強い結合を達成するための適切な候補です[24–26]。ただし、プラズモン空洞との単一分子の結合は、理論と実験の両方で大きな課題であり、結合システム内の分子の位置を操作することは困難です。

この論文では、青色離調トラップシステムの各ユニットについて、準単一分子とプラズモン空洞の間の強い結合を理論的に研究します。ブルーデチューントラップシステムは金ナノホールアレイで構成されており、各ユニットは1つの分子のみをトラップします。有限差分時間領域（FDTD）法を使用して構造をシミュレートし、透過スペクトルを取得できます。分子が最も弱い点でトラップされると、散乱スペクトルは、強い結合レジームの特徴であるラビ分裂を示します。提案された構造は、光トラップシステムの準単一分子とプラズモン空洞の間の強力な結合を実現するための潜在的な方法を提供します。

メソッド

青で離調したトラッピングを実現するために、周期的なナノホール構造を設計します。シミュレーションはFDTD法に基づいており、EAST FDTDソフトウェアを採用して構造を設定し、透過スペクトルと電磁分布を調査します。私たちのモデルでは、半径Rの一連の金ナノホールユニットが X の2次元（2D）Au膜に配置されています。 - Y 平面とAu膜の厚さは400nmです。格子定数 L と半径 R それぞれ1000nmと250nmです。シミュレーション中、バックグラウンドインデックスは1で、グリッドは各方向で5nmです。周期境界条件は、両方の X に沿って設定されます -軸と Y -軸。 Z に沿って完全一致レイヤーが設定されます -軸。完全一致層の数は32です。Auの誘電率はJohnsonとChristyから得られます[27]。円偏光は通常、 Z に沿って提案された構造の表面に注入されます -軸、波長は696nmです。 X - Y 平面レコーダーは、提案された構造物の表面から400 nm離れており、透過率と X を計算します。 - Z 電磁界分布を取得するために、プレーンレコーダーが構造の中央にあります。 FDTDシミュレーション[28–30]の双極子源の特性により、双極子源を使用して分子をシミュレートできます。分子の共鳴波長は707nmで、減衰率は1.1×10 ¹⁴ です。 Hz。私たちのシミュレーションでは、トランスミッション T は、上面のポインティングベクトルを積分し、金属構造がない場合に得られたものに正規化することによって計算されます[31]。 FDTDシミュレーションで計算された透過率は T で表されます。 =私 _T /（私 _C + 私 _D ）、ここで I _T は送信の電磁界強度です。 I _C は円偏光の電磁界強度であり、 I _D は双極子の電磁界強度です。

結果と考察

トラッピング構造

サブ波長の穴の配列を備えたプラズモンナノ構造は、ナノ穴の近くの局所電場を大幅に強化する並外れた光透過効果を示します[32–34]。この効果を分子運動に使用します。プラズモン共鳴場が分子共鳴から青く離調すると、分子の巨大な反発力が発生し、構造表面から約数百ナノメートル離れたトラップが生成されます。図1に示すように、私たちのアプローチを示すために周期的なプラズモンナノ構造を設計します。

周期的プラズモンナノ構造の概略図

このセクションでは、分子を使用しないシミュレーション結果についてのみ説明します。通常、 Z から構造物を照らすために、円偏光を使用します 無限遠の方向で、透過スペクトルは図2に表示されます。

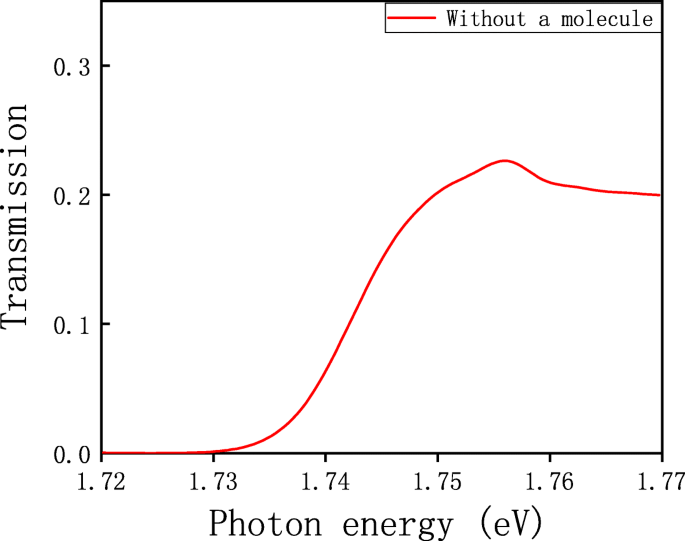
分子のない構造の透過スペクトル

共鳴ピークは707nm（1.756 eV）で観察されます。これは、ユニット（ホール）間の相互作用に起因します。このピークは、ウッドアノマリーの（1、1）次の波長に近い[35]。サブ波長ホールのアレイは、SPPへのブラッグ散乱を持ち、位相整合条件を満たすことができるアレイの逆格子ベクトルをもたらします[20]。したがって、入射光はSPPを励起する可能性があり、SPPを励起するこの方法は、Kretschmann構造を使用するよりもはるかに簡単であり、金属の厚さの影響を受けません。システムの空間電磁界分布を調査する目的で、| E の図をプロットします。 | ² X の配布 - Z Y の平面 707nmの共振波長で=0。これは図3aに示されています。

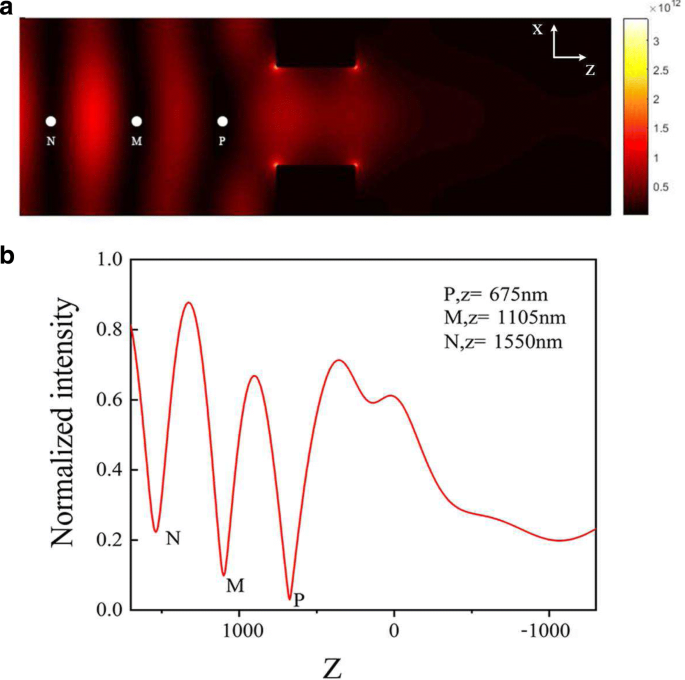
a 電磁界強度| E | ² X での配布 - Z Y の平面 =0 λ =696nm。 b | E の正規化された強度分布 | ² 対 Z X で =0および Y = X では0 - Z 平面

図3aには、| E の最小値が3つあります。 | ² 白い点P、M、およびNで示されます。これらの3つの最小値の出現は、プラズモンナノホールのアレイによる光の近接場散乱から生じるホットスポットに起因する可能性があります。実際、電磁場の分布は、表面プラズモン場とナノホールを通る空間電磁場の重ね合わせです。 | E の曲線 | ² 対 Z X で =0および Y = X では0 - Z 平面も図3bにプロットされています。空間電磁分布のシミュレーション結果によると、3つの強度の最小値があります。これは、青色で離調した光トラップを意味します。

分子は、青色に離調した光による光双極子力を介して、電磁場強度の最小値にトラップできます。私たちのシミュレーションでは、分子は2レベルのシステムとして扱われ、FDTDシミュレーションで双極子としてシミュレートできます[28–30]。トラップの可能性 U _opt 分子の場合、電磁場に関連する反発する光双極子ポテンシャル E 、[1、4]で与えられます：

ここで、α 分極率が低下します。この場合、α =−7.87×10 ⁻³⁸ F ・ m ² [20]。したがって、電磁界強度分布に基づいて、トラップ電位を取得できます。式を使用して。 （1）および| E | ² 図3aの分布では、両方の X の線に沿ったトラップポテンシャルを計算しました。 =0および Y =0図4に表示されているように。

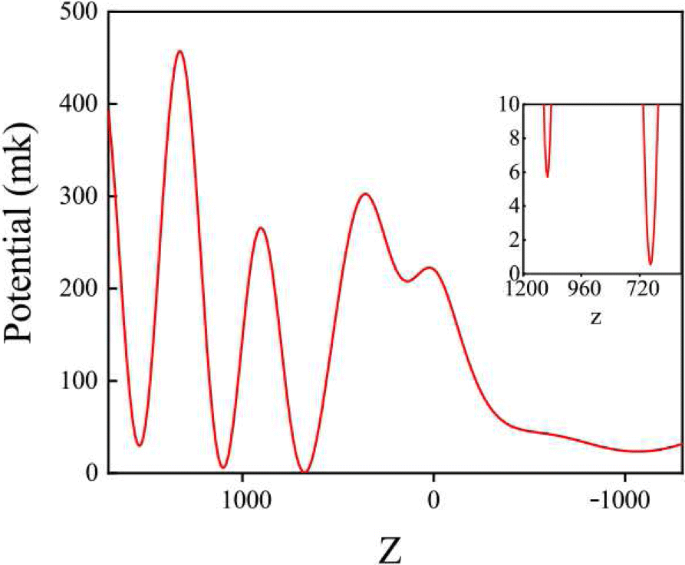
X のトラップポテンシャル - Z Y の平面 =0。挿入画像は、トラップの可能性が最も低いもののスケールアップです

図4では、最低強度の位置が点Pにあることがわかります。ここでは、入射パワーは P として設定されています。 _i =120 mW、トラップ電位は0.53mKです。 Chen etal。 ⁸⁷ R b 2.02mKのトラップポテンシャルで安定してトラップできます[20]。これらのパラメーターを比較すると、ブルーデチューントラップシステムは、分子量が約400のローダミン分子をトラップできます。上記の分析に照らして、ポイント（0、0、675 nm）でのトラップ位置と概略図を選択します。構造に閉じ込められた分子の図を図5に示します。

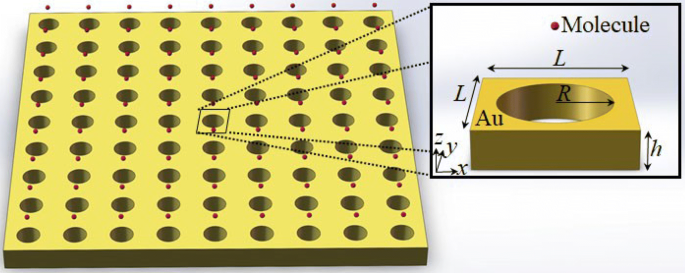
構造に閉じ込められた分子の概略図

構造と分子間の強力な結合

分子は私たちの構造の各ユニットに配置され、強い結合レジームでの光と分子の相互作用を研究します。この分子は、FDTDシミュレーションでは双極子として扱うことができます。図3aに示すように、表面から275nm離れた電位最小点Pに双極子を追加します。双極子の分極は X に沿っている可能性があります -軸、 Y -軸、または Z -軸。分子の共鳴波長は707nm（1.756 eV）です。まず、 Z に沿った双極子の分極について考えます。 -軸。透過スペクトルも取得され、結果は図6に示されています。

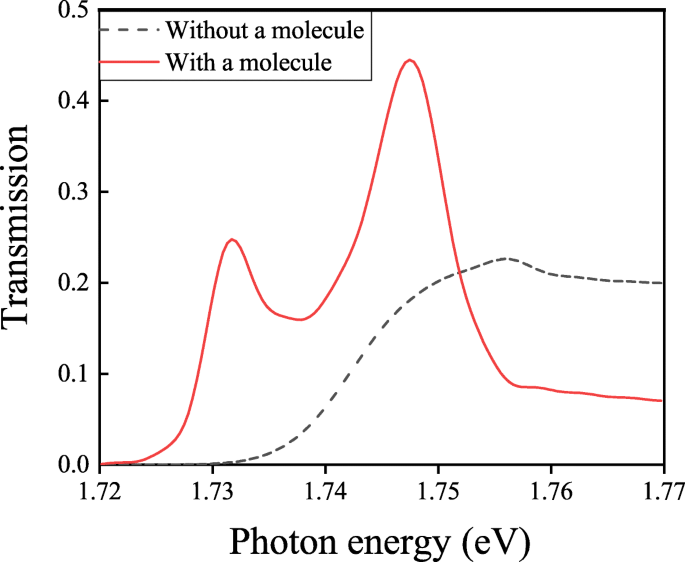
分子がある場合とない場合の透過スペクトルは、点Pでトラップされます

比較のために、各ユニットに分子がない構造の透過スペクトルも図6にプロットされています。図6に沿って、分子がある構造の透過スペクトルに2つの分割ピークが見られます。ラビ分割線形状と強い結合現象を示します。入射光は構造物の表面に入射するだけでなく、分子を励起します。入射光によって励起されたSPPは、動作波長付近で分子によって励起されたSPPと結合します。これらの2種類のSPPは互いに結合し、透過スペクトルに2つの分割ピークを形成します。透過曲線の線形は、強い結合現象を示しています。一般的に、これら2つの分割ピークの周波数ω _± [36、37]として示されます：

ここでω ₀ は、孤立した分子と空洞が共鳴していると仮定した場合のエネルギーです。γ _c =4.08×10 ¹³ Hz [38]およびγ _m =1.1×10 ¹⁴ Hzは、それぞれプラズモン空洞と分子の崩壊率であり、 g は結合定数です。 g では強い結合が発生します> 0.5 | γ _c − γ _m |そして、有限の寿命を持つ服を着た状態の形成に対応します。提案する構造では、結合定数 g は144meVですが、0.5 | γ _c − γ _m | 143meVです。以前の作品では、ラビ分割はΩとして示されていました =| ω ₊ − ω ₋ | J凝集体-金属または分子-金属ハイブリッドナノ構造に基づく構造では、100〜450 meVの領域にあります[39、40]。ラビ分割は結合強度 g に関連しています 、これは\（\ sqrt {N / V} \）に依存します。ここで、 N は分子の数であり、 V それぞれモードボリュームです[37]。私たちの仕事では、提案された構造とモードボリューム V の各ユニットに1つの分子しかありません。 ラビがΩを分割するほど大きい は約16meVであり、この分裂は、金属-半導体ハイブリッドナノ構造[41]および金属-2D材料システム[42]の強い結合に匹敵します。また、 X に沿った分子の分極と構造の強い結合を研究しました -軸と Y -それぞれ軸。シミュレーション結果を図7に示します。

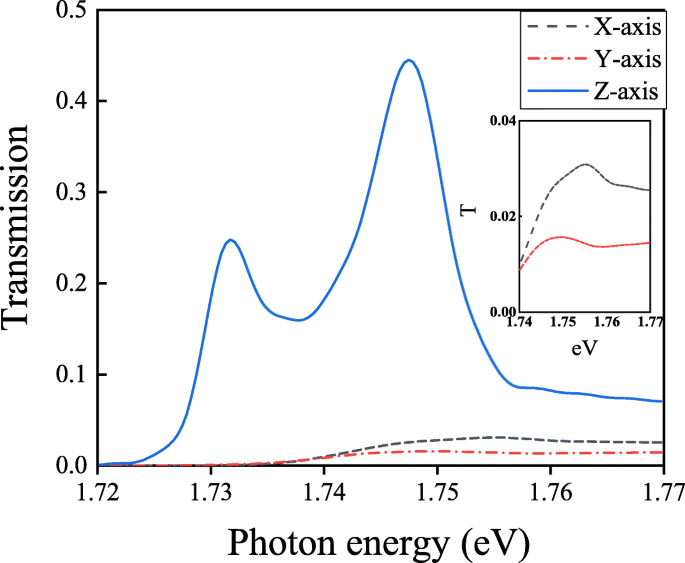
X、Y、Z方向にそれぞれ偏光した分子の透過スペクトル

図7では、2つの分割ピーク（710 nm、1.747 eV、717 nm、1.717 eV）は、 Z に沿った分子の分極を伴う構造にのみ現れます。 -軸。 X に沿って分極した分子 -軸または Y -軸は、AuナノキャビティまたはAuナノホールアレイと結合する前に強力な集合的挙動を示します。集団行動 S _k X に沿って分極した分子の -軸または Y -軸は結合双極子法[43]で計算できます：

ここで k ₀ は真空中の波数ベクトルθです。 は2つの双極子間の角度であり、 r = n L 、 n =1、2、3 ...ここで、条件は\（\ lambda =\ frac {L} {\ sqrt {i ^ {2} + j ^ {2}}} \）（ i 、 j =0、1、2、...、ただし両方 i および j 同時に0に等しくない）、集合的振る舞いは非常に大きく、これは式（1）に特異点を示します。 （3）[35、43]。これは、透過スペクトルに共鳴ディップを示します。 X に沿って分極した分子の場合 -軸または Y -軸、集合的な振る舞いは、分子とプラズモン空洞の間の結合を弱めるには大きすぎます。波長707nm（1.756 eV）付近の透過スペクトルでは、（1、1）のオーダーの木材異常[35]のオーダーのみが見られ、強い結合は現れませんでした。したがって、 Z に沿って分極した分子のみ -提案された構造の軸は、強い結合現象を生成する可能性があります。分子の共鳴波長を変更すると、以下の手順で青色離調トラップシステムの強い結合を得ることができます。第一に、分子の共鳴に従って、ナノホールアレイの格子定数を固定することができます。第二に、青色離調トラップシステムの動作波長も決定できます。これは、金属ナノホールアレイの格子定数に依存します。第三に、電磁場分布を取得して、トラップ位置を見つけます。最後に、分子を最適なトラップ位置に配置して透過スペクトルを計算すると、強い結合線形を持つ透過が得られます。

結論

要約すると、金属プラズモンブルーデチューントラップシステムを設計し、準単一分子とトラップシステム間の強い結合現象を調査します。 FDTDシミュレーションでは、分子として双極子源を使用し、電磁界分布に従って、構造内の1つの分子のみをトラップするための最適な位置を見つけることができます。分子がトラップされているかどうかにかかわらず、提案された構造の透過率を計算すると、分子が構造にトラップされている場合は透過スペクトルに2つの分割ピークがあり、分子がトラップされていない場合は1つのピークしか観察されないことがわかります。 。 2つの分裂ピークは、強い結合が起こったことを示しています。したがって、量子情報処理に応用できる可能性のあるナノプラズモニック構造で強い結合を実現するために、青色離調トラップシステムを設計することができます。

略語

FDTD：

有限差分時間領域