ナノクラスターの魔法の数学的関係

はじめに

ナノクラスターのマジックナンバーと公式には、1969年のvanHardeveldとHartogによる先見の明のある出版物にまでさかのぼる長い歴史があります[1]。彼らの洞察は、ナノサイエンスの時代よりも前のものでした。それ以来、マジックナンバーは2Dポリゴンと3D多面体[2]、カーボンフラーレン[3]、そして限られた範囲でクラスター[4]に現れるのを見てきました。シリコン[5]、ホウ素[6]などの多様な資料、および実際にはインデックスサービス「Webof Science」からの1000を超える出版物は、クラスター内の魔法数に言及しています。ナノクラスターのサイズと形状の研究は、今日の社会にとって重要です。これは、固有の物理的および化学的特性だけでなく、光学、触媒、電子、および磁気のアプリケーションとの関連性も決定するためです[7]。私たちの目的は、ナノ領域に入った今、この知識のデータベースを現在の関係とデータで更新することです。

ナノクラスターでの魔法数の発生は、主に基本的なセル上での原子の殻の形成と関係があります。原子の数が完全な殻を完成させると、原子の殻を定義する「魔法」と呼ばれる固有の数のセットが見つかります。クラスターは、原子を頂点、結合をエッジとするグラフで表されます。タマネギの層のような入れ子になった殻で構成されています。レイヤーの数を n と定義します n の関数として、最近傍の配位数、結合、原子の総数、およびいくつかのトポロジカルインデックスの数学的関係を発見します。 。 vanHardeveldとHartogによる元の論文[1]は、fcc、bcc、およびhcpクラスターを検討しました。 TeoとSloaneによる参照[2]は、多面体と正多面体を考慮していますが、最近傍配位数の関係を無視しています。位相幾何学的特性とクラスターの分散に加えて、単純立方晶、ダイアモンド立方晶、および正多面体を調べることにより、このデータベースに追加します。

バルクから数個の原子のクラスターへのサイズの遷移は、実際にはバルク原子と比較した表面原子の関係に関するものです。触媒化学、表面プラズモン共鳴、光学量子ドットフォトルミネッセンス[8]などの特性は、表面原子の配位と数の影響を受けます。表面原子の分散または相対パーセンテージは、以前に検討されたように、原子の総数に対する表面原子の比率によって決定されます[9]。私たちの分析は、クラスターの形状に関する分散の相対的なランク付けを決定します。

トポロジカルインデックスは、ウィーナーのインデックスとパラフィンの沸点に関するWienerの元の論文から始まりました[10]。細谷がトポロジカルインデックスを分析するために数学的形式を導入したのは、しばらくしてからでした[11]。以前にトポロジカルインデックスとナノクラスターを導入しました[12]。この記事を書いている時点では、多くのインデックスが存在し、そのうちのいくつかは隣接行列または距離行列に依存しています。ここでは、クラスターの形状の多くで、 n の関数として4つのインデックスに魔法の数学的関係が存在することを示します。 とシェルの数。

メソッド

調査するクラスターのタイプごとに、クラスターの原子座標を決定する計算アルゴリズムを作成します。次に、次のように定義された隣接行列と距離行列の作成に進みます。隣接行列 A i を定義する場所に作成されます および j r を要求することにより、最も近い隣人としてそれらを他の人から分離します _ij < r _c 、ここで r _c はしきい値であり、最近傍距離よりわずかに上ですが、2番目の隣接距離よりも小さくなっています。したがって、

ここで r _ij は原子 i 間のユークリッド距離です およびアトム j 。 r の適切な値 _c は1.32・ r _分 、ここで r _分 は最小の結合長です。これは、十二面体構造だけでなく、私たちが研究している他の構造にも当てはまります。クラスターの配位数は、隣接行列の列にあるゼロ以外の要素の数です。距離行列は

として定義されます $$ \ mathbf {D}（i、j）=\ left \ {\ begin {array} {ll} 0＆i =j \\ d_ {ij}＆i \ neq j \ end {array} \ right。 $$（2）

ここで d _ij i からのグラフの最短経路の長さです j へ 。隣接行列から距離行列を計算するための効率的なアルゴリズムが存在します[13]。これらの定義を使用して、Wienerインデックス W を計算できます。 （ G ）、ハイパーウィーナーインデックス、 W W （ G ）、逆ウィーナーインデックス rW （ G ）、およびセゲドインデックス Sz （ G ）、以前に詳述したように[14]。これらの計算では、トポロジカルインデックスとナノクラスターに以前使​​用したものと同じアルゴリズムを使用します[12]。

以前の著者は、ここに提示された作業に関連する、私たちの記法で凝縮した魔法の関係の証明を提供しました[1、2]。最近傍隣接行列を作成するので、配位数 c がわかります。 n _i 頂点の i A の要素を合計する （ i 、:)。私たちの構造は n で構成されています 0、1、…、 n の番号が付けられた+1シェル 。 \（\ phantom {\ dot {i} \！} N _ {{cn} _ {i}}（n）\）を配位 c の原子数とします。 n _i ここで、1≤ c n _i ≤ c n _M c で n _M クラスター内の最大の調整。次に、クラスター内の原子の総数は

で与えられます。 $$ N_ {T}（n）=\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {N _ {{cn} _ {i}}（n）}。 $$（3）

外殻の表面原子 n バルク調整よりも少ない結合のセットがあります。したがって、表面原子の最大配位は c です。 n _s < c n _M 、および表面原子の数は

$$ N_ {S}（n）=\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {s}} {N _ {{cn} _ {i}}（n）}。 $$（4）

これは、すべての非サーフェス頂点の調整が c より大きい場合に当てはまります。 n _s 、これはすべてのクラスターに当てはまりますが、以下の12面体の不一致に注意してください。合計が c である隣接行列の列を数えることにより、\（\ phantom {\ dot {i} \！} N _ {{cn} _ {i}}（n）\）を決定します。 n _i 。クラスタ座標アルゴリズムはシェルによって構築されているため、後続の各シェルには、以前の n の低い値がすべて含まれていることに注意してください。 。図1に、fccキューブと12面体のクラスターのシェルを示します。さらに、クラスター内の結合の数は

です。 $$ N_ {B}（n）=\ frac {1} {2} \ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {{cn} _ {i} \ cdot N _ {{cn} _ {i}}（n）}、$$（5）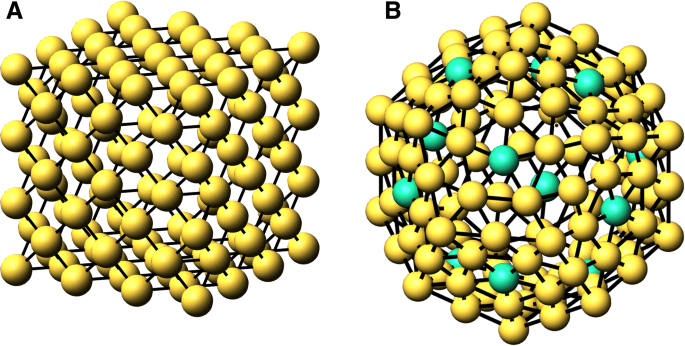

n の原子の殻 =A.fccキューブおよび n の場合は3 =2B。十二面体。 Bでは、緑色の原子（12）は c を指します n =シェル内で5

ここで N _B （ n ）は結合の数であり、 c n _M 最大の調整です。 1/2の係数は、ペアワイズ最近傍結合のために発生します。この魔法の関係は、[4]で調べられたいくつかのクラスターを除いて、以前の出版物では考慮されていなかったようです。また、TeoとSloaneは、クラスターの原子、表面原子、内部原子の総数を次のように導き出したとコメントしています[2]：

$$ N_ {T}（n）=\ alpha n ^ {3} + \ frac {1} {2} \ beta n ^ {2} + \ gamma n + 1 ~~ n \ ge {0} $$（ 6）

ここで N _T （ n ）は原子の総数であり、

$$ \ alpha =C / 6 $$（7）

ここで C 多面体が分割される四面体セルの数であり、

$$ \ beta =1 / 2F_ {s} $$（8）

ここで F _s は表面上の三角形の面の数であり、

$$ \ gamma =F_ {s} / 4 + V_ {i} + 1-C / 6 $$（9）

ここで、 V _i 内部の頂点の数です。彼らはまたそれを示しています

$$ N_ {S}（n）=\ beta n ^ {2} + 2 ~~ n \ ge {1}; ~~ N_ {S}（0）=1 $$（10）

および

$$ N_ {I}（n）=N_ {T}（n）-N_ {S}（n）、$$（11）

ここで N _私 （ n ）は内部原子の数です。この情報（式（11））は、隣接行列と式（11）に含まれています。 （3、4、5）。これらの方程式は、隣接行列データからの結果のチェックです。中心多面体については、

もあります。 $$ N_ {I}（n）=N_ {T}（n-1）、$$（12）

と式から。 （11）、

$$ N_ {T}（n）=N_ {S}（n）+ N_ {S}（n-1）+ ... + N_ {S}（1）+ N_ {S}（0）。 $$（13）

これらの方程式から、次のように各クラスターの魔法の公式を導き出すことができます。トポロジカル（0,1）隣接行列 A を計算した後 n のクラスターの場合 説明したように、シェルのサイズは N = N _T （ n ）は原子の総数を示します。列 i のエントリの合計 結合の数を与える c n _i （ n ）アトム i の場合 c に等しい列の合計の数を数えます n _i （ n ）は明らかに\（\ phantom {\ dot {i} \！} N _ {{cn} _ {i}}（n）\）を与えます。これらは n に依存することがわかっているので 最大3次の多項式として、 N を計算できます。 _T （ n ）および c n _i （ n ） n の4つの連続した値の場合 、 n と言います = n ₀ + j 、 j =0,1,2,3。単純な補間多項式は、多項式係数を与えます。 n を増やすことによって確認する必要があります ₀ 、通常は1に等しい、数式は変更されません。数式が n から安定した場合 ₀ オンにすると、すべての n が保持されます ≥ n ₀ 。場合によっては、多項式の関係は偶数の n に対してのみ成り立ちます。 値または奇数。たとえば、fccの菱形十二面体（表1）の場合、 n の場合、連続するシェルには3つの配位を持つ8つの原子があります。 ≥2は偶数であり、 n の場合はなし 奇妙です。このような場合、 n には異なる多項式関係が成り立ちます。 偶数および n 奇妙ですが、データは n に使用されます = n ₀ + j 、 j =0,2,4,6、 n ₀ 奇数（例： n ₀ =1）または n ₀ 偶数（ n ₀ =2）。正確な有理係数を取得するには、MATLABのシンボリックツールボックスを使用して、正確な算術演算でファンデルモンドシステムを解いて係数を求める必要があります。これは、表2、3、4、5、1、6、7、8、9、10、11、12、13、14、15、16、17、18、および19の計算方法です。次のセクションでは、 N の魔法の公式を決定します _T （ n ）、 N _B （ n ）、および\（\ phantom {\ dot {i} \！} N _ {{cn} _ {i}}（n）\）の場合、禁止されているレシピに従います。

<図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図> <図>

表面原子の分散（露出率、FE）は次のように定義されます。

$$ \ text {FE} =\ frac {N_ {S}} {N_ {T}} \ cdot 100 \％$$（14）

ここで N _S は表面原子の数であり、 N _T は原子の総数です[9]。相対的なクラスターサイズを次のように定義することで、異なるクラスターを比較できます。

$$ d_ {rel} =b（N_ {T}）^ {1/3}; ~~ b =d_ {at} ^ {-1} \ cdot \ left（\ frac {6V_ {u}} {\ pi n_ {u}} \ right）^ {1/3} $$（15）

ここで d _at は共有結合原子半径、 V _u はユニットセルの体積であり、 n _u はユニットセル内の原子の数です。結晶構造定数 b fccおよびhcpクラスターの場合は1.105、bccクラスターの場合は1.137 [1]、単純な立方クラスターの場合は1.488、ダイアモンド立方クラスターの場合は1.517になります。上に示したように、FEの式は、クラスターの2次と3次の比率であり、 d に対するべき乗則のカーブフィットによってモデル化できます。 _rel 。変数 d _rel 結晶構造に関係なく、異なるクラスターを相互に比較することができます。結晶ユニットセルがない一部のプラトンクラスターでは、変数として\（N_ {T} ^ {1/3} \）を使用します。

結果と考察

金属ナノクラスターのサイズと形状の研究は、20年前の幼少期から進化してきました。表20は、2018年現在の関連する進捗状況を示しています。

表には、Fe ₂ のみが存在する、切り詰められた六角形の双角錐を除いて、合金や化合物ではなく、主に遷移金属を示しています。 O ₃ 発見された。その特性と安定性のために、他のどの元素よりも多くの金クラスターの合成がありました。以下のサブセクションでは、魔法の公式とクラスターの種類に関連する特定のトピックに限定して説明します。

FCCクラスター

プラズモン貴金属と重要な触媒活性元素を含む、8つの遷移金属がfcc構造で結晶化します。以下の表21を参照してください。ナノクラスター合成の大部分は、これらの要素を使用して行われました。さまざまな形状とサイズのfcc要素の合成のリファレンスを表21に示します。

これらの元素の合金も興味深いですが、これらの参照はここで引用するには多すぎます。多くの場合、合成される一般的な形状は、立方体、八面体、立方八面体、および二十面体です。通常、（111）表面は通常、（100）表面よりもエネルギーが低いため、（111）ファセットを持つクラスターは合成が容易です[7]。 fccの菱形十二面体については、偶数と奇数の式が存在することがわかります。 「 n 」を置き換えると、これらは[1]の結果と一致します。 」を2（ m -1）。 [24]にリストされているfcccuboctahedraの式は、私たちと同じマジックナンバーを生成しますが、シェルに n として番号を付けるため、1だけシフトされます。 =1,2、…そして番号付け n を使用します =0,1、…。私たちの魔法の公式は[2、4]のものと一致し、以前に公開された作品を尊重し、数学の連続性を維持するために、[2、4]表記を使用します。 5つのfccクラスター形状とそれに関連する魔法の公式を以下に示します。

BCCクラスター

周期表の遷移金属のうち7つはbcc構造を持っています。表21を参照してください。磁性元素Fe、Co、およびNiのうち、鉄だけがbccです。鉄のナノキューブは、これまでに合成された唯一のbccクラスター形状であるように見えます[25]。鉄のバルク構造はbccですが、fccナノクラスターが合成されています[26]。このリファレンスでは、クラスターの熱力学的安定性も分析しています。ここでは、5つのbccクラスター形状とそれに関連する魔法の公式を示します。

HCPクラスター

12個の遷移金属はhcp構造を持っています。表21を参照してください。ただし、これらの多くは酸化するか、合成するための説得力のある科学的関心を欠いています。表11の六角形の双ピラミッド型クラスターの形状に関しては、金のクラスターが合成されています[27]。関連する切り詰められた六角形の双角錐は、αによってのみ形成されたようです。 −fe ₂ O ₃ [28]。

プラトニッククラスター

正多面体は古代ギリシャ人から知られています。それらには、立方体、四面体、八面体、二十面体、および十二面体が含まれます。前の表に、fccおよびbccキューブと八面体の魔法の公式を示しました。ここでは、二十面体、十二面体、四面体、および体心四面体の式を示します。 「方法」のセクションで前述したように、十二面体はここで分析されたクラスターに固有であり、 c n _s =7は、表面原子とバルク原子の両方を指します。図1bに、外殻に5倍と6倍の両方の配位原子が含まれていることを示しました。シェルが内部になると、これらの5倍および6倍に配位した原子は、いずれかの側のシェルへの結合で7倍および8倍に配位します。また、6重に配位した外側のシェル原子は、内側のシェルに結合することで7倍に配位します。したがって、12面体には7倍の表面およびバルク配位原子があります。構造内の各シェルには12個の5重シェル原子があり、12 n を生成します。 −12個のバルク7重配位原子。残りの7つの配位は表面原子です。

金のナノクラスターは正多面体の形をとることが示されています[29]。このリファレンスには、立方体、四面体、八面体、および二十面体が含まれます。その後、黄金の十二面体ナノクラスターも合成されました[30]。ここでは、その c で「fccのような」正四面体の両方を示します。 _M =12 fcc構造の場合と同様に、表16の体心四面体では、緑色の原子が単結合を持っています。プラトンの魔法の公式を以下に示します。

ダイアモンドキュービック、シンプルキュービック、および十面体クラスター

元素シリコンとゲルマニウムは、ダイヤモンドの立方格子と、炭素のダイヤモンド同素体を持っています。特に、水素終端シリコンが最近注目されています。クラスター内の立方体形状につながる（100）水素終端表面は、エネルギーが最も低いと判断されています[31]。サイズが8〜15nmのSi-Hナノキューブの合成が達成されました[32]。表17は、水素終端Si-Hクラスターの図を示しており、単結合の水素原子が緑色で表示されています。ナノクラスターがダイアモンドの立方体の形状をとる場合、単一のダングリングボンドが存在し、構造を維持するために不動態化する必要があります。魔法の公式を見ると、そのようなSi-Hクラスターの構成は\（\ phantom {\ dot {i} \！} \ text {Si} _ {8n ^ {3} + 6n ^ {2} -9n +5} \ text {H} _ {12n-8} \）、ここで n はクラスター内のシェルの数です。このような半導体量子ドットは、光学特性にとって重要である可能性があり、水素終端クラスターのサイズに伴うバンドギャップの変化は、クラスターサイズに反比例することが決定されています[33]。

単純な立方格子構造は、以前に他の人によって分析されました[4]が、詳細は提供していません。以前に d を調査しました 次元の超立方体が形成されます[14]。ポロニウムは、単純な立方構造をとる唯一の元素です。放射性であるため、特殊な用途につながる可能性があります。ここでは、ダイアモンドキュービック、単純キュービック、および十面体クラスターの魔法の公式を示します。

魔法の位相幾何学的公式

結晶の構造の複雑さを測定することで、構造の単純さや複雑さを知ることができ、適切に使用することで関連する構造をランク付けできます。このようなランク付けについては、「方法」のセクションで説明したように、結晶格子のグラフィカルな説明を検討することが役立ちます。結晶構造のトポロジーの複雑さは、グラフの頂点次数分布 I によって測定されます。 _vd [34]、ソフトウェアToposPro、バージョン5.3.2.2 [35]を使用：

ここで a _i i の程度（調整）です 頂点と合計はすべての v に沿って進行します 商グラフの頂点。このパラメーターは、これまで検討してきたクラスターとは対照的に、無限の結晶を使用しますが、さまざまな結晶構造の相対的な複雑さを測定するのに役立ちます。したがって、グラフの数値が大きいほど、またはグラフの情報量が多いほど、グラフは複雑になります。表22に、 I の値を示します。 _vd Crystallographic OpenDatabaseの結晶構造のcifファイルから派生したToposProから取得。ポロニウムは単純な立方構造で結晶化する唯一の元素であり、値はゼロです。つまり、商グラフには1つの頂点とゼロのエッジがあり、私たちが期待することと一致して、単純な立方構造は実際に最も複雑でない構造です。塩のNaClも示され、単純な立方構造の2つの元素と、ダイヤモンド立方のシリコン、fccの金、bccの鉄、hcp構造のコバルトが示されています。シャノンエントロピーに関連する別の複雑さの尺度[34]は、すべての要素のこの尺度がまったく同じであるため、役に立たないことに言及します。

トポロジカルインデックスを記述する魔法の公式には、魔法の公式を決定するための「方法」のセクションで説明したのと同様の方法を適用できます。ここでのみ、多項式の次数は7、8、または9であるため、少なくとも10個の連続する n の値 -値を計算する必要があります。次に、より高度な内挿問題が結果をもたらします。シンボリックツールボックスを使用してサイズ10×10の線形システムを解くには時間がかかるため、トポロジカルインデックスのすべての係数は、複数の右辺を使用して同時に計算し、すべての多項式の係数を取得できます。

トポロジカルインデックスの魔法の公式は、表23、24、および25に詳しく説明されています。分析する4つのインデックスは、 n のみに依存します。 、クラスター内のシェルの数。結果を見ると、最も複雑でない構造としての単純な立方格子にも「最も単純な」式があります。私たちの努力にもかかわらず、bccキューブのセゲドインデックスを解決することはできません。安定した解決策は見つかりませんでした。一般に、fcc構造は、トポロジー式を解くのが簡単です。 hcp構造は解決できず、bcc構造はわずかしか解決できませんでした。これは、fcc格子がbccまたはhcpよりも単純であるため、トポロジの複雑さに関連している可能性があります。表22を参照してください。表内に、立方八面体、二十面体、および十面体の式を示します。以前[12]は、これらのインデックスの数値データの表を提供しましたが、[12]の立方八面体は異なるマジックナンバーを持っていることに注意してください。ここでは、表形式のデータが魔法の公式として簡潔に要約されていることがわかります。また、インデックスの多項式の次数は、3D空間の規則に従います[14]。正多面体のいくつかのトポロジカルインデックスは以前に公開されています[36]。このリファレンスから、 n の5つのソリッドすべてのウィーナーインデックスを検証します =1。 fcc格子の単位格子の列のウィーナー指数が研究されていますが[37]、クラスターを研究しているため、結果を比較することはできません。

分散

さまざまなクラスターの表面原子（分散、FE）のパーセンテージを図2に示します。白金ナノクラスターは、サイズと形状に依存する酸素還元反応（ORR）に対して触媒活性を持つことが知られています[38]。この参照により、サイズが2.2nmの白金立方八面体クラスターが最大のORR活性を示すことがわかりました。 PtNi合金の場合、ORRには（111）表面が好ましいことも知られています[39]。 d でのFEの二十面体、八面体、十面体、および立方八面体のクラスターを比較します。 _rel =2.2nmの白金の場合は7.5。二十面体、八面体、および十面体のクラスターには、（111）面の表面があります。図2のべき乗則を使用して、与えられた d を求めます。 _rel 二十面体クラスターのFEは47.9％、立方八面体クラスターのFEは52.8％、十面体クラスターのFEは57.5％であり、八面体クラスターのFE =58.9 ％ 。したがって、形状に基づいて、八面体クラスターは（111）表面と、同様のサイズのFEの最高値の両方を持ちます。べき乗則係数と指数の両方が、小さい d のFEの決定に関連しています。 _rel 。べき法則の指数の数学的解釈は、縦座標FEと横座標 d の関係としての物理的重要性を示します。 _rel 、または d の相対変化率に対するFEの相対変化率 _rel 。べき法則係数は、 d のときのFEの値です。 _rel =1。

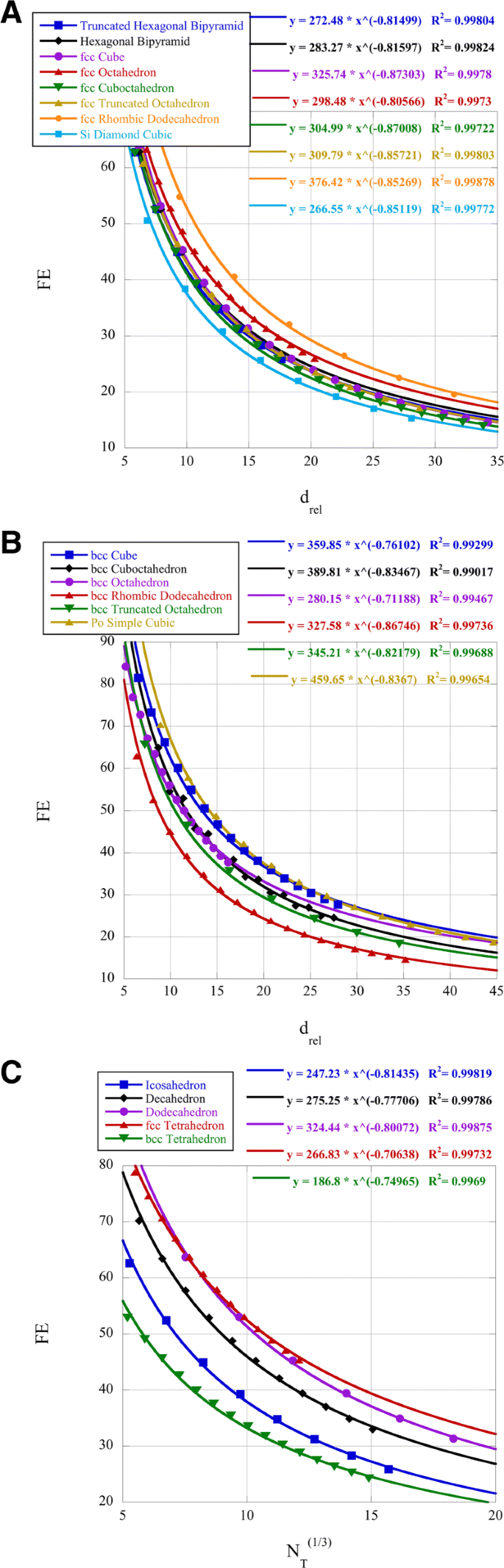
ナノクラスターの分散FE

別の研究グループは、白金合金の二十面体クラスターを合成し、その活性を八面体のものと比較しました[40]。これらのナノクラスターのサイズは約13nmまたは N でした =八面体クラスターの場合は20,000、 N 二十面体クラスターの場合は=15,000。これにより、 d が生成されます _rel =八面体クラスターの場合は30、二十面体クラスターの場合は25。関連するべき法則を使用すると、これによりFE =18.0 ％が得られます。 八面体の場合は19.8％、二十面体クラスターの場合は19.8％です。このサイズのクラスターのFEにはほとんど違いはありませんが、二十面体クラスターには双晶によるかなりのひずみがあり、これによりdバンドの中心がシフトし、ORRの結果に影響を与える可能性があります[40]。ただし、[38]のサイズ依存データを考えると、クラスターが小さいほど、さらに高いORRデータが生成されることが示唆される場合があります。実際、4 nm Pt ₃ Ni八面体をMoでドープすると、記録的な高ORR結果が得られました[41]。

結論

19種類のナノクラスターと、原子数、結合数、配位数、トポロジカルインデックスに関連するいくつかの魔法の公式を研究しました。これらには、fcc、bcc、hcp、正多面体、ダイアモンド立方、単純立方、および十面体クラスターが含まれます。これらの結果の大部分は以前に決定されたものよりも詳細であり、多数が初めて列挙されます。材料関連の研究の大きな目標は、構造と特性の相関関係です。ナノクラスターの魔法の関係に関するこの詳細な研究は、その方向への一歩です。例として、表面原子の分散とその触媒活性との関係についての説明があります。これらの結果が、科学者がナノクラスター構造と関連する特性を研究するのに役立つことを私たちは意図しています。

略語

bcc：

体心立方

cif：

結晶学的情報ファイル

fcc：

面心立方

FE：

露出した部分、分散

hcp：

六角形の最密充填

ORR：

酸化還元反応

rW（G）：

リバースウィーナーインデックス

Sz（G）：

セゲドインデックス

W（G）：

ウィーナーインデックス

WW（G）：

ハイパーウィーナーインデックス