表面波が進行するグラフェン層に対する粒子の速度ロック効果

はじめに

最近、一連の表面波/フォノンによって誘発される高速輸送および拡散現象がマイクロ/ナノスケールで検出されています。最初に、カーボンナノチューブ[1,2,3,4,5]またはグラフェンリボン[6,7,8,9,10]に沿った熱泳動現象が広範囲に調査されました。熱ゆらぎは、カーボンナノチューブ（CNT）の表面に沿って軸方向の温度勾配を課すことにより、カーボンナノチューブ（CNT）を通る連続的な水流を可能にすることが確認されています[11、12、13]。非平衡分子動力学シミュレーションは、大きなグラフェン基板上の温度勾配を利用して小さなグラフェンナノフレークの運動を制御する可能性を調査するために行われます[6]。さらに、グラフェンおよび六方晶窒化ホウ素（h-BN）表面での熱駆動水滴輸送は、分子動力学シミュレーションによって研究されています[8、9]。これらの現象は、フォノンの特定のモードと相関することが示唆されています[14、15、16、17、18、19]。たとえば、Schoen etal。カーボンナノチューブ内の熱泳動運動は、チューブの呼吸モードに起因すると考えられています[1,20]。パニゾンら。 [21]グラフェン上の屈曲進行波/フォノンは、その運動量を吸着質に渡し、輸送を引き起こす可能性があると指摘しました。熱泳動現象と同様に、Angelos等。グラフェン上での温度による伝播リップルは、液体水中の水分子の自己拡散よりも2〜3桁速い水ナノ液滴の高速拡散につながる可能性があることを示しました[22、23]。

熱ゆらぎに加えて、研究により、振動がカーボンナノチューブ（CNT）の内外で粒子や液滴を輸送できることが確認されています[24、25、26、27]。たとえば、直線偏光された横方向の音波が線形運動量をナノ液滴に通過させると、ナノ液滴は30 nm / nsに近い速度でナノチューブに沿って輸送されます[24、28]。 Guo etal。振動するカンチレバー内の水分子は遠心力によって駆動され、分子動力学シミュレーションによってCNTの固定端から自由端まで連続的に流れることができることを実証しました[26、29]。単層カーボンナノチューブ（SWCNT）を介した水分子の新しいナノスケールの一方向輸送は、振動電荷と非対称表面エネルギーを持つ複合SWCNTを使用して設計されています[30]。周ら。 [31]は、機械的振動を動力源とする単層カーボンナノチューブに基づくナノサイズのウォーターポンプの電流反転を調査し、水流が機械的振動の周波数に敏感に依存することを確認しました。 ChangとGuo [32]は、カーボンナノチューブのドミノ波を発見しました。この波は、最大1 km / sの高速で内部分子を発射することができます。可逆的なドミノプロセスは、単層カーボンナノチューブでも証明されています[33]。

熱ゆらぎや振動によって引き起こされるさまざまな高速拡散・輸送現象がナノスケールで検出されていることから、表面の上下運動が拡散・輸送を促進できることが確認されています。波と粒子の動きの関係はまだ不明であり、統一することはできません。主な説明は、表面の運動量が表面の外側の粒子または液滴に輸送される可能性があるということです[22、24]。しかし、この説明からは、振幅、周波数、粒子と表面の相互作用の関係を理解することはできません。さらに、Angelos等。グラフェン表面での吸着質の高速拡散には、グラフェンの曲率の1つの兆候を明確に優先する必要があることを指摘しました[22]。これは、波状の表面形態によって引き起こされる相互作用ポテンシャルが高速拡散と密接に関連していることを示しています。したがって、波状の表面と外側の粒子の間の相互作用を調査することは、ナノスケールでの高速輸送と拡散のメカニズムを理解するために非常に重要です。

この論文では、レナードジョーンズ（L–J）ペアポテンシャルによって表されるvdW相互作用に基づいて波状グラフェン表面の外側の粒子を研究することにより、波状運動と粒子の速度の間のコヒーレントな関係をMDシミュレーションによって示します。波状の表面に落下する粒子の全体的な速度は、特定の前提条件、つまり速度ロック効果を使用して、進行波と同じに保たれることが確認されています。次に、曲率の関数として表される粒子と波面の間の相互作用ポテンシャルに基づいて、ポテンシャル水たまり理論が構築されます[34、35、36]。この理論では、速度ロック効果の2つの前提条件が提案され、潜在的な水たまり理論によって予測される軌道と速度は、MDシミュレーション結果とよく一致します。また、波長と振幅、およびvdW相互作用パラメーターの影響が分析され、グラフェン表面での液滴サーフィン現象で検出された規制とよく一致していることが示されています[22]。波動による速度ロック効果のメカニズムは、粒子速度と波状表面の間の新しいコヒーレントな関係を明らかにします。

メソッド

MDシミュレーションは、ソフトウェアパッケージLarge-scale Atomic / Molecular Massively Parallel Simulator（LAMMPS）に実装されています。波状の表面は、原子番号密度が\（\ rho =3.85 \ times 10 ^ {19} \、{\ text {m}} ^ {-2} \）のグラフェン層であると想定されています。グラフェンシートは最初は z で平らです =0Å、 x に沿った長さは6344Å 方向、結果として6000原子の単位格子サイズになります。 y軸に沿って 周期境界条件は、12.2Åの周期長で使用されます。ここでは、モデルを単純化し、波状の表面。最初は、パーティクルは z に配置されます =7Åおよび x =200Å。初速度は z で-50m / sです。 -方向と x で約2000m / s -方向。 z で初速度の開始時間を設定する -方向、波状の表面に落下する粒子の初期位置を制御できます。

グラフェン原子のモデル化には、反応性経験的結合次数（REBO）ポテンシャルが採用されています[37]。一方、レナードジョーンズポテンシャルは、粒子\（P \）とグラフェンの各炭素原子間の相互作用を次のようにモデル化するために選択されます。

ここで、\（\ varepsilon =5.92 \ times 10 ^ {-21} \、{\ text {J}} \）および\（\ sigma =4 \ times 10 ^ {-10} \、{\ text {m}} \）。粒子\（P \）と曲面の間の平衡高さは、法線力の条件によって決定される\（h =4.2 \ times 10 ^ {-10} \、{\ text {m}} \）と見なされます。ゼロおよびシミュレーション結果として、追加ファイル1：1で詳しく説明されています。

進行波関数は、次のように正弦波形式を取ります。

ここで、振幅は\（A =1 \ times 10 ^ {-9} \、{\ text {m}} \）と見なされ、波長は\（\ lambda =21.75 \ times 10 ^ {-9} \、 {\ text {m}} \）特に記載がない限り。角周波数は\（\ omega ={{2 \ pi} \ mathord {\ left / {\ vphantom {{2 \ pi} {10 ^ {-12}}}} \ right。\ kern- \ nulldelimiterspace } {10 ^ {-12}}} \）10psの期間に対応します。したがって、波の速度は\（v _ {{{\ text {wave}}}} =2175 \、{\ text {m}} / {\ text {s}} =\ lambda \ omega / 2 \ pi \） 。進行波をトリガーするには、グラフェンの左側の10Å（つまり、 y \（\ in \）[− 10、0]Å）は z で小刻みに動く -上記の振幅と周波数の方向。さらに、 x の炭素原子>6010Åは、グラフェンシートを安定させるためにクランプされています。特に、平らなグラフェンシートをシミュレートする場合は、クランプされていないグラフェン原子も z に沿った初期位置につながれます。 -ばね定数が0.0938eV //Å2の弱い軸（ A 以外） 0に設定されます。

固定されていない炭素原子には、5Kの初期温度が割り当てられています。この温度は、グラフェンの曲げモードと伸縮モードの間の調和結合によって引き起こされる熱的に活性化されるリップルを排除し、機械的励起によって引き起こされる進行波の影響に焦点を当てるために設定されます[22]。次に、構造は1 fsのタイムステップでミクロカノニカルアンサンブル（NVE）に進化します。この進化を監視したところ、シミュレーション全体を通して温度はほとんど変化していませんでした。

結果と考察

波状のグラフェン表面と平坦なグラフェン表面上の粒子の軌跡を図1に示します。時間間隔は、波状の表面の周期と見なされます。粒子の相対位置は、波の山または谷を基準にして変化しないことがわかります。これは、粒子が波の速度に等しい速度で波状の表面にロックされていることを意味します。比較として、平らな面でのパーティクルの全体的な動きは、同じ初期位置の波状の面での動きよりも明らかに遅いです。粒子の速度は、摩擦のために平らな表面では急速に低下しますが、波状のグラフェン表面の粒子では摩擦が機能していないようです。シミュレーション温度と波動関数のパラメーターが異なるその他のMDシミュレーションケースは、追加ファイル1：1に示されています。原子Xeと分子C ₆₀ のシミュレーション 波状で平らな表面での移動は、この現象の一般化可能性を確認するために行われ、追加ファイル1：2に示されています。

波状および平坦なグラフェン表面上の粒子の軌道

ナノスケールでのスピードロック効果のメカニズムを理解するために、波状表面 S 間の相互作用を考慮してモデルを構築します。 および外部粒子 P 、図2a、bに示されています。波状の表面の波長と振幅が\（\ lambda \）と A であると仮定します。 、それぞれ、 P 間の最も近い高さ および S h です 、 S の数密度 は\（{\ rho} _ {s} \）です。 MDシミュレーションでは、粒子 P 間の相互作用 波状の表面はvdW相互作用と見なされ、L–Jポテンシャルで表されます。

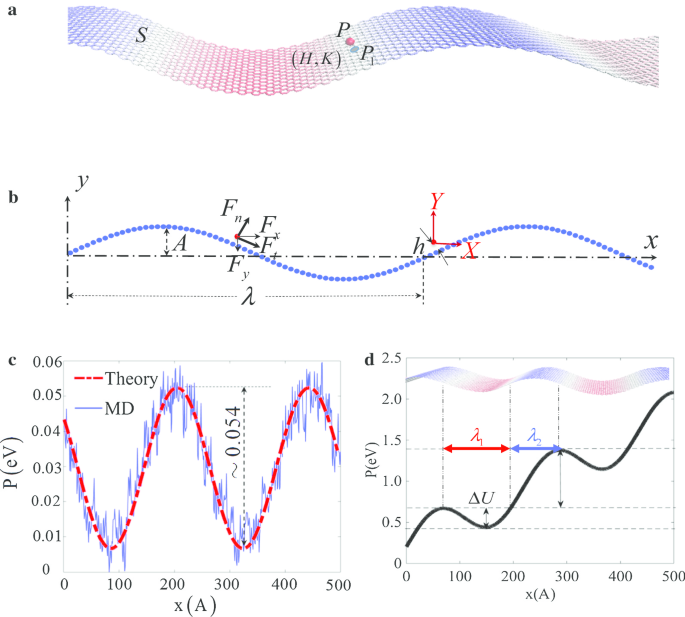
ジオメトリ構成とポテンシャル分布。 a 波状の表面の3Dモデル S および外部粒子 P 最も近い点 P ₁ 表面上; b 波状表面の2Dモデル S とパーティクル P ; c 波状表面の相互作用ポテンシャルの比較 S および外部粒子 P 式によって。 （1）およびMDシミュレーション。 d PXY の相対ポテンシャル分布 コーディネート

次に、 P 間の相互作用 および S L–Jペアポテンシャルに基づく平均曲率とガウス曲率の関数として記述されることが証明されています[34,35,36]、

ここで、点\（P_ {1} \）は、サーフェス S で最も近い点です。 パーティクル P 、および H と\（K \）は、それぞれ点\（P_ {1} \）での平均曲率とガウス曲率です（図2a）[20]。この曲率ベースのポテンシャル[Eq。 （3）]は、マイクロ/ナノスケールでの多くの異常現象の説明に使用されてきました[38、39]。 （3）この場合、上記のパラメータについてMDシミュレーションの表面電位と比較することで検証され、図2cに表示されます。

粒子 P に対する波状表面の影響を分析する前に 、摩擦を調査して考慮に入れる必要があります。粒子と波面の間の摩擦は、ナノスケールでは非常に複雑になる可能性があります[39、40、41、42、43]。摩擦の原始的な推定は、追加ファイル1：3で詳しく説明されているように、MDによって平らなグラフェン層上の粒子の動きをシミュレートすることによって行われます。便宜上、ここでは波状の表面ではなく平らな表面を使用します。この概算は、追加のファイル1：3で、さらに潜在的な水たまりメカニズムと組み合わせて推定されます。上記のパラメータを使用すると、摩擦は\（f =--5.2 \ times 10 ^ {-13} \、{\ text {N}} \）として推定されます。

次に、表面 S 間の相対ポテンシャル とパーティクル P 摩擦を考慮して調査します。まず、図2bに赤い色で示されているように、相対的な波フレーム座標\（PXY \）が作成されます。これは、波の速度で移動するため、進行波に対して静止したままになります。したがって、進行波は\（PXY \）で「凍結」されます。粒子はグラフェンを基準にして右方向に移動し続けるため、粒子に作用する摩擦は常に表面に沿って左方向になります。結果として、相対的な波動フレームポテンシャルは、曲率ベースのポテンシャルから摩擦によって行われる仕事を差し引いたものになります。

曲率ベースのポテンシャル U を代入する _n と方程式への摩擦。 （4）、相対的な波動フレームポテンシャルを評価することができ、図2dに描かれています。

波枠座標 PXY 進行波、粒子の初期位置 P に沿って移動します ポテンシャルの中で粒子の軌道を決定します。粒子の初速度 P は\（v_ {0} \）で、波の速度は\（v _ {{{\ text {wave}}}} \）です。図2dに基づいて、2つの前提条件を提案できます。粒子の初期位置\（ P \）レッドゾーンの潜在的な水たまりに位置します\（\ lambda_ {1} \）;初期の波動フレームの運動エネルギーは\（\ frac {1} {2} m \ left（{v_ {0} --v _ {{{\ text {wave}}}}} \ right）^ {2} \ leを満たす\ Delta U \）。そうすると、パーティクルは水たまりから飛び出すことができなくなりますが、代わりに水たまりの中に閉じ込められてぐらつきます。絶対座標の観点からは、粒子\（P \）は潜在的な水たまりで振動しますが、波の速度の周りにロックされた速度によって伝播する波とともに動き続けるため、スピードロック効果があります。それ以外の場合、粒子の初期位置\（P \）がブルーゾーン\（\ lambda_ {2} \）または相対的な初期運動エネルギー\（\ frac {1} {2} m \ left（{v_ { 0} --v _ {{{\ text {wave}}}}} \ right）^ {2}> \ Delta U \）、パーティクル\（P \）は単一の水たまりの中に留まらず、左に跳ねて下の水たまりに移動します波枠ポテンシャル面に沿って。絶対座標の観点では、粒子は、力の別の平衡が満たされるまで、伝播する波の後ろに遅れます。このような平衡の1つの可能性は、粒子がグラフェン上で移動を停止し、摩擦がなくなることです。興味深いことに、点灯している[21]。パニゾンら。速度差がある場合、進行波は粒子によって散乱され、推進力を提供することを明らかにします。これは、粒子の最終速度がゼロより大きいことを示唆しています。

私たちの理論を定式化し、よりよく説明するために、粒子Pの運動方程式は、ニュートンの運動の法則によってさらに確立されます。粒子に作用する駆動力 P 垂直抗力\（F _ {{\ text {n}}} \）と接線力\（F _ {{\ text {t}}} \）の2つの部分、つまり（図2b）

L–Jポテンシャルの場合、原子間に引力相互作用と反発相互作用の両方が存在し、外部粒子\（P \）は高さ h に留まります。 法線力\（F _ {{\ text {n}}} \）がゼロの場合、高さ h の決定計算 追加ファイル1：2に入れられます。すると、粒子\（P \）の\（x \）方向の運動方程式は次のようになります。

ここで、\（F_ {x} \）は、\（x \）方向の接線力\（F _ {{\ text {t}}} \）の成分です（図2b）。式の計算（6）は粒子の軌道を与えます。正弦波表面の場合、ガウス曲率はゼロであり、平均曲率は\（Ozx \）表面の曲線の曲率に等しくなります。つまり、\（K =0 \）および\（H =\ kappa \）[52]に置き換えられます。式（5）から（6）へ、粒子 P の移動軌道 数値的に解くことができます。

ロックとロック解除の例を図3に示します。図2dのロック領域\（\ lambda_ {1} \）に対応する初期位置（図3a）について、理論結果とMDシミュレーション結果の軌跡を比較します。図3b。これは、粒子が摩擦のために非常に短い時間で平らなグラフェン表面上を移動しなくなり、粒子が波面上を右方向に移動し続けることを示しています。そして、理論的な軌道は、MDシミュレーションの結果に近似しています。この傾向は、シミュレーション時間の10倍で示された粒子の速度について図3cでさらに確認されます。粒子はロッキングゾーンに落下し、初速度は波の速度に等しいため、潜在的な水たまりで振動し、全体の速度は波の速度に等しくなります。これは、私たちの推測によるものです。初期位置（図3d）が図2dのロック解除領域\（\ lambda_ {2} \）にある粒子の場合、波面上の粒子の軌道は一定になる傾向があり（図3e）、さらに確認されます。速度分布。進行波が、平坦なグラフェン表面での粒子の動きと比較して、速度ロック解除領域に当たった場合でも、粒子の動きを強化できることは興味深いことです。図3fは、シミュレーション時間よりも長い時間、速度がゼロに減少することを示しています。その他の例は、追加ファイル1：3に示されています。

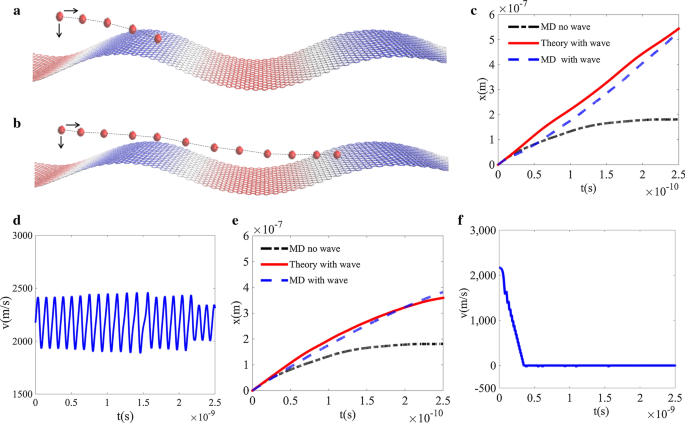
ロックとロック解除の例。 a 初期粒子速度が\（v_ {0} =2175 \、{{\ text {m}である波状グラフェン表面の速度ロック領域\（\ lambda_ {1} \）に粒子がどのように着地するかを示す概略図} \ mathord {\ left / {\ vphantom {{\ text {m}} {\ text {s}}}} \ right。\ kern- \ nulldelimiterspace} {\ text {s}}} \）; b 粒子が波状グラフェン表面の速度ロック解除領域\（\ lambda_ {2} \）にどのように着地するかを示す概略図。 c MDシミュレーションと理論の両方による粒子の軌道、平坦なグラフェン上の粒子の軌道も比較のためにプロットされます。 d 式による粒子速度の時間発展。 （6）; e MDシミュレーションと理論の両方による粒子の軌道。 f 式による粒子速度の時間発展。 （6）

潜在的な水たまりのメカニズムによると、粒子の速度ロック効果は潜在的な波の表面によって支配されます。パラメータの影響は、潜在的な水たまり理論に基づいて議論することができます。明らかに、これらには波長\（\ lambda \）、振幅 A が含まれます 、周波数\（\ omega \）およびL–Jポテンシャルパラメータ。以下の分析では、摩擦は異なるパラメータに関して同じままであると想定されていることに注意してください。異なる波長の電位分布 A 、振幅\（\ lambda \）とL–Jポテンシャルパラメータ\（\ varepsilon \）をそれぞれ図4に示します。図4aは、潜在的な水たまりの深さが\（\ lambda \）の増加とともに減少し、波長が臨界値を超えると速度ロック範囲がなくなることを示しています。また、低い周波数\（\ omega \）は大きい\（\ lambda \）に関連するため、速度ロック範囲は\（\ omega \）の増加とともに減少します。図4bは、 A の増加に伴って潜在的な水たまりの深さが増加することを示しています。 、振幅が小さすぎると速度ロック効果がなくなります。比率 A / \（\ lambda \）は、損傷を防ぐために大きすぎないようにする必要があります。通常、\（\ lambda \）と A の両方 波や粒子のスケールが大きくなると大きくなります。スケール効果を調べるために、比率\（\ lambda \）/ A を維持します。 修正して、さまざまな\（\ lambda \）または A の影響を調べます 。図4cは、\（\ lambda \）または A の増加に伴い、潜在的な水たまりの深さが急速に減少することを示しています。 。これは、曲率に基づく駆動力がスケールの増加とともに急速に減少することを示しているため、粒子の速度ロック効果は、大規模な波のある表面では消滅します。 L–Jポテンシャルパラメータ\（\ varepsilon \）については、ペア相互作用ポテンシャルが強いとスピードロック領域が広くなり、ペア相互作用ポテンシャルが弱いとスピードロック効果がなくなることが確認されています（図1）。 4d）。

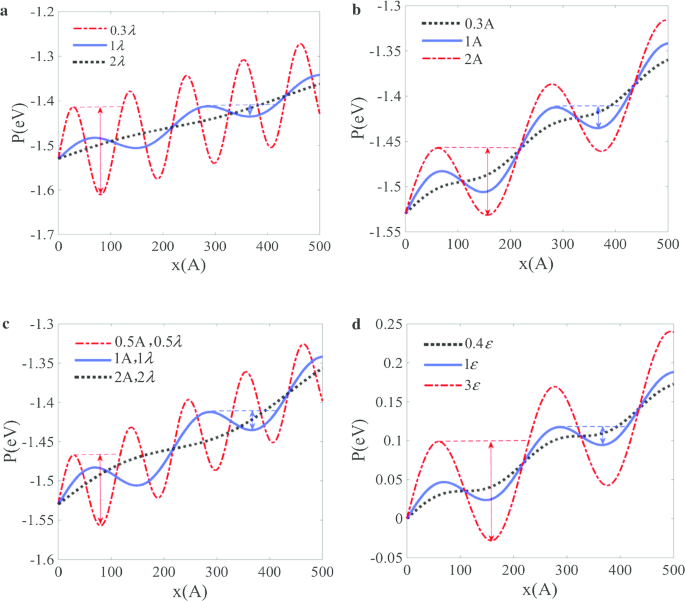
潜在的な公開に対するパラメータの影響： a 波長の影響; b 波の振幅の影響; c 波長と振幅の比率の影響。 d L–Jポテンシャルパラメータの効果

剛性とL–Jポテンシャルパラメータは他の2Dナノ材料では異なり、周波数と波の速度が異なることに注意してください[44]。パラメータ分析によると、波状の表面に適切な波長と振幅を選択することで、潜在的な水たまりが現れます。潜在的な水たまりは、波状の表面で移動する粒子の前提条件であるため、この速度ロック効果は、短距離相互作用の下で多くの2Dナノマテリアル層にも確立されます。

この論文では1つの粒子の動きについて説明しますが、それはまだ熱環境の枠内にあります。潜在的な水たまりは、粒子と表面の間の結合運動に不可欠な条件です。複数の粒子の場合、それらがすべて潜在的な水たまり領域にあり、前提条件を満たしている場合、それらはトラップされ、波状の表面とともに移動します。パラメータ効果によると、粒子の動きは、波長と振幅を調整することによって制御できます。波長が小さく、振幅が大きく、周波数が高い表面波では、速度ロック領域が大きくなるため、波状表面での高速拡散も強化されます。パラメトリック分析は、他の多くの文献で検出された高速拡散規制にも準拠しています。たとえば、Angelos etal。拡散係数はグラフェン表面のリップル振幅とともに増加することが指摘されています[22]。彼らは、波紋の振幅が増加し、谷に対する液滴の優先度が増加していることを確認しました。これは、図4bで説明できます。振幅が十分に大きくなると、速度ロック領域はおそらく波長全体をカバーし、拡散を強化します。さらに、谷のポテンシャルは常に山のポテンシャルよりも小さいことを指摘しました[22]（図4）。これは、図4に示す山の領域のポテンシャルが低いことに対応しています。Caoetal。進行する表面波の存在下でのナノチャネル内の流体の流れを研究し、振幅と周波数の増加とともに速度が増加することを確認しました[45]。これもパラメトリック分析によるものです。

MDシミュレーションは、非常に短時間でのみ特性を反映できます。このスピードロック効果のより多くの潜在的なアプリケーションは、潜在的な水たまりメカニズムから推測できます。例えば、振幅と周波数を調整することにより、粒子を動かしたり停止させたりすることができるほぼロックまたはロック解除領域を実現することが可能です。垂直方向の表面の波状の動きは、横方向の粒子の動きに変換することができ、これは一種のラチェット運動に類似しており、ナノ電気機械システムで使用できることに留意されたい。さらに、粒子と表面の相互作用が動きに影響を与えるため、波状の表面によって強化される軌道は、ペアポテンシャルが異なる粒子では異なり、フレーズの分離につながる可能性があります。

結論

結論として、我々は、進行する表面波、すなわちスピードロック現象を伴う粒子とグラフェン層の間の独特の関係を示しています。 MDシミュレーションにより、一定の条件で粒子の速度を波の速度付近に保つことができることを確認しました。潜在的な表面の水たまりがロック効果を支配するメカニズムを解明するために、理論モデルが構築されています。ロック条件は、このモデルに基づいて提案されます。つまり、粒子の初期位置は潜在的な水たまりに位置し、初期の運動エネルギーは粒子を潜在的な水たまりから飛び出すように駆動することはできません。理論的予測によって予測された粒子軌道は、MDシミュレーションの結果とよく一致しています。波長と振幅の影響、およびL–Jポテンシャルパラメータについて説明します。この作品はまた、波状の表面での高速拡散と輸送、およびフレーズ分離の潜在的なアプリケーションを理解するための新しい視点を提供します。

データと資料の可用性

この調査中に生成または分析されたすべてのデータは、この公開された記事[およびその追加ファイル]に含まれています。

略語

MD：

分子動力学

vdW：

ファンデルワールス

CNT：

カーボンナノチューブ

h-BN：

六方晶窒化ホウ素

SWCNT：

単層カーボンナノチューブ

L–J：

レナードジョーンズ

LAMMPS：

大規模な原子/分子の大規模並列シミュレータ

REBO：

反応性の経験的結合次数

NVE：

ミクロカノニカルアンサンブル