より大きな5変数および6変数のカルノー図

より大きなカルノー図は、より大きな論理設計を減らします。どれくらいの大きさで十分ですか？これは、入力の数、ファンインによって異なります。 、検討中の論理回路に。大規模なプログラマブルロジック企業の1つが答えを持っています。

顧客の設計ライブラリから抽出されたアルテラ独自のデータは、異質性の価値をサポートしています。アルテラは、ロジックコーンを調べ、それらをLUTベースのノードにマッピングし、各ノードで最適な入力の数で並べ替えることにより、ファンインの分布が2〜6の入力間でほぼフラットで、ピークが良好であることを発見しました。 5時。

答えは、ほとんどすべての設計で6入力以下、平均的な論理設計で5入力以下です。 5つの変数カルノー図が続きます。

5変数Kマップ

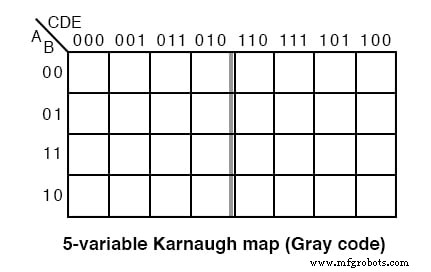
5つの変数Kマップの古いバージョンであるグレイコードマップまたは反射マップを上に示します。マップの上部（および6変数マップの場合は側面）には、完全なグレイコードで番号が付けられています。グレイコードは、コードのほぼ中央を反映しています。このスタイルマップは古いテキストにあります。新しい推奨スタイルは以下のとおりです。

Kマップのオーバーレイバージョン

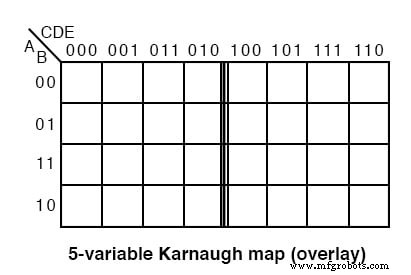
上に示したカルノー図のオーバーレイバージョンは、上部の3ビットアドレスの最上位ビットを除いて、単純に2つ（6変数マップの場合は4つ）の同一のマップです。

マップの上部を見ると、番号が以前のグレイコードマップとは異なることがわかります。 3桁の数字の最上位桁を無視すると、シーケンス 00、01、11、10 オーバーレイマップの両方のサブマップの見出しにあります。 8つの3桁の数字のシーケンスはグレイコードではありません。最下位2ビットのうち4つのシーケンスはですが。

5変数のカルノー図を使用してみましょう。 5ビットのバイナリ入力（A、B、C、D、E）を持ち、AがMSB（最上位ビット）である回路を設計します。入力データで検出された素数に対して、出力ロジックHighを生成する必要があります。

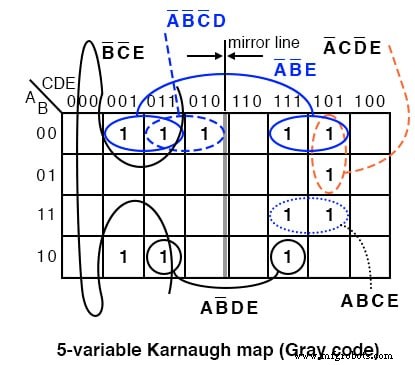
参考までに、古いグレイコード（反射）マップに上記の解決策を示します。素数は（1,2,3,5,7,11,13,17,19,23,29,31）です。 1 をプロットします 対応する各セルで。次に、セルのグループ化に進みます。簡略化した結果を書き込んで終了します。

4セルグループA’B’Eは、ミラーラインの両側にある2対のセルで構成されていることに注意してください。同じことが2セルグループAB’DEにも当てはまります。鏡面反射による2セルのグループです。このバージョンのKマップを使用する場合は、マップの残りの半分で鏡像を探してください。

Out =A’B’E + B’C’E + A’C’DE + A’CD’E + ABCE + AB’DE + A’B’C’D

以下に、5変数マップのより一般的なバージョンであるオーバーレイマップを示します。

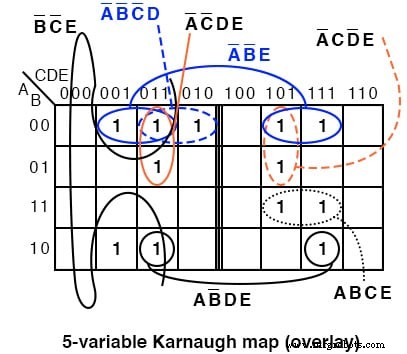
2つのマップのパターンを比較すると、マップの上部のアドレス指定が異なるため、マップの右半分のセルの一部が移動します。また、マップの2つの半分の間の共通点を見つけるために別のアプローチを取る必要があります。

マップの半分を残りの半分の上にオーバーレイします。上のマップから下のマップへのオーバーラップは、潜在的なグループです。次の図は、グループAB’DEが2つの積み重ねられたセルで構成されていることを示しています。グループA’B’Eは、2つの積み重ねられたセルのペアで構成されています。

A’B’E の場合 4セルのグループ ABCDE =00xx1 グループのために。つまり、A、B、Eは同じ 001 それぞれグループのために。そして、 CD =xx つまり、それはさまざまであり、 CD =xx には共通点がありません 4セルのグループの場合。 ABCDE =00xx1 以降 、4セルのグループは A’B’XXE =A’B’E でカバーされます 。

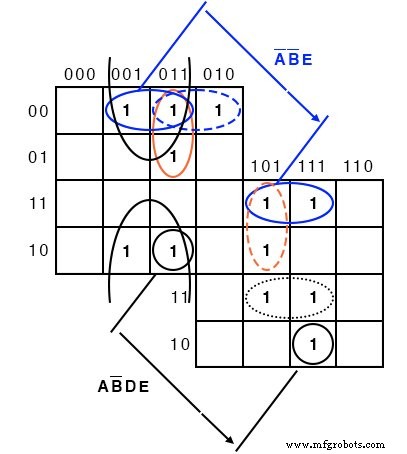
上記の5変数オーバーレイマップは積み重ねて表示されています。

6変数のカルノー図の例を次に示します。 4つのサブマップを精神的に積み重ねて、 Out =C’F ’に対応する4つのセルのグループを確認しました。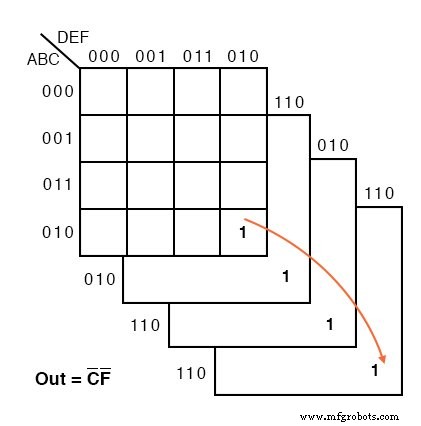

マグニチュードコンパレータ（6変数Kマップを示すために使用）は、2つの2進数を比較し、3つのそれぞれの出力で互いに等しいか、大きいか、または小さいかを示します。 3ビットのマグニチュードコンパレータには2つの入力A ₂ があります。 A ₁ A ₀ およびB ₂ B ₁ B ₀ 集積回路のマグニチュードコンパレータ（7485）には、実際には4つの入力がありますが、以下のカルノー図は適切なサイズに保つ必要があります。 A> B のみを解決します 出力。

6変数Kマップ

以下では、6変数のカルノー図が3ビットのマグニチュードコンパレータのロジックを単純化するのに役立ちます。これはオーバーレイタイプのマップです。マップの上部と左側にあるバイナリアドレスコードは、完全な3ビットのグレイコードではありません。

4つのサブマップの2ビットアドレスコードはグレイコードですが。 4つのサブマップを互いに積み重ねて冗長な式を見つけます（上に表示）。以下の例ではありませんが、4つのマップすべてに共通のセルが存在する可能性があります。サブマップのペアに共通のセルがあります。

上記のA> B出力は、下のマップのABC> XYZです。

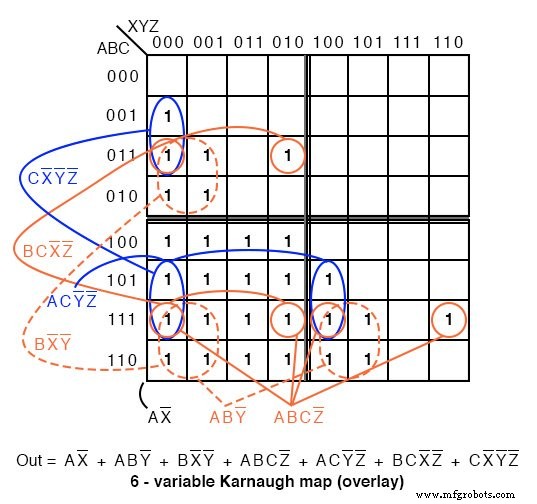
どこでも ABC XYZ より大きい 、 1 プロットされます。最初の行で ABC =000 XYZ のどの値よりも大きくすることはできません 。いいえ 1 この行のs。 2行目では、 ABC =001 、最初のセルのみ ABCXYZ =001000 ABC XYZ より大きい 。単一の 1 2行目の最初のセルに入力されます。 4行目、 ABC =010 、 1 のペアがあります s。 3行目、 ABC =011 3つの 1 があります s。したがって、マップは 1 で埋められます s ABC が存在するすべてのセル XXZ より大きい 。

セルのグループ化では、可能であれば、隣接するサブマップでグループを形成します。 16セルの1つのグループを除くすべてのグループには、サブマップのペアからのセルが含まれます。次のグループを探します：

• 16セルの1グループ
• 8セルの2つのグループ
• 4セルの4つのグループ

16セルのグループ、 AX ’ 右下のサブマップのすべてを占めます。ただし、上の図では丸で囲んでいません。

8セルの1つのグループは、左下のマップの同様のグループに重なる上部のサブマップの4セルのグループで構成されます。 8セルの2番目のグループは、右のサブマップの4セルの同様のグループで構成され、左下のマップの4セルの同じグループをオーバーレイします。

4セルの4つのグループは、関連する製品用語とともに上記のカルノー図に示されています。 8セルの2つのグループと16セルのグループの製品用語とともに、7つの用語すべての最終的な製品の合計の削減が表示されます。

1 を数える sマップには、合計16 + 6 + 6 =28のものがあります。 K-mapロジックの削減前は、SOP出力には28の積項があり、それぞれに6つの入力がありました。カルノー図は、4つ以下の入力の7つの積項を生成しました。これこそが、カルノー図のすべてです！

配線図は表示されていません。ただし、4つのTTLロジックファミリパーツを使用したABC> XYZ用の3ビットマグニチュードコンパレータのパーツリストは次のとおりです。

• 1 ea7410トリプル3入力NANDゲートAX ’、ABY’、BX’Y ’
• 2 ea 7420デュアル4入力NANDゲートABCZ ’、ACY’Z’、BCX’Z ’、CX’Y’Z’
• 1 ea 7430 7-P-termの出力用の8入力NANDゲート

レビュー：

• ブール代数、カルノー図、およびCAD（コンピューター支援設計）は、論理を単純化する方法です。ロジックの簡素化の目標は、最小限のコストのソリューションです。
• 最小コストのソリューションは、最小の入力数で最小のゲート数を使用した有効なロジック削減です。
• ベン図を使用すると、ブール式を視覚化できるため、カルノー図への移行が容易になります。
• カルノー図のセルはグレイコードの順序で編成されているため、ブール式の冗長性を視覚化して簡略化することができます。
• より一般的なSum-Of-Products（Sum of Minters）式は、単一のORゲート（sum）に供給するANDゲート（product）として実装されます。
• Sum-Of-Products式（AND-ORロジック）は、NAND-NAND実装と同等です。すべてのANDゲートとORゲートはNANDゲートに置き換えられています。
• あまり使用されないProduct-Of-Sums式は、単一のANDゲート（積）にフィードするORゲート（合計）として実装されます。 Product-Of-Sums式は、 0 に基づいています s、maxterms、カルノー図。