カルノー図のセルを気にしない

これまで、入力条件が完全に指定された場合の論理削減の問題について検討してきました。つまり、3変数の真理値表またはカルノー図には2 ⁿ がありました。 =2 ³ または8エントリ、完全なテーブルまたはマップ。

一部の現実の問題については、必ずしも完全な真理値表に記入する必要はありません。表全体に記入しないこともできます。

たとえば、4ビットとしてエンコードされたBCD（Binary Coded Decimal）番号を処理する場合、BCD範囲（0、1、2…9）を超えるコードは気にしない場合があります。 16進数（Ah、Bh、Ch、Eh、Fh）の4ビット2進コードは、有効なBCDコードではありません。

したがって、必要がなければ、真理値表またはKマップの最後にこれらのコードを入力する必要はありません。

これらのコード（1010、1011、1100、1101、1110、1111）は、BCDでエンコードされた数値のみを処理している限り存在しないため、通常はこれらのコードを入力する必要はありません。これらの6つの無効なコードは気にしない 私たちに関する限り。

つまり、これらのドントケアに対して論理回路が生成する出力は関係ありません。

気にしないでください

カルノー図や真理値表では気にしないでください。 1 sまたは 0 s、入力条件に対する出力が何であるかを気にしない限り、予期しない入力条件になります。通常の 1 の中で、これらのセルをアスタリスク*でプロットします。 sおよび 0 s。

セルのグループを形成するときは、ドントケアセルを 1 として扱います。 または 0 、またはドントケアを無視します。

これは、ドントケアなしで可能であるよりも大きなグループを形成できる場合に役立ちます。すべてまたは一部のドントケアをグループ化する必要はありません。

ロジックを単純化する場合にのみ、グループで使用してください。

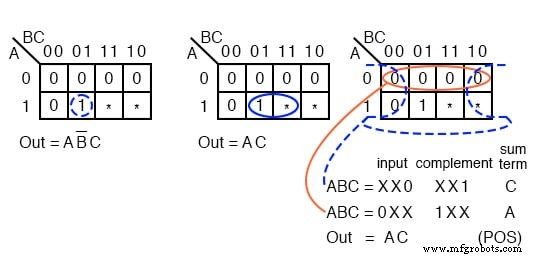
上記は、目的の出力が 1 である論理関数の例です。 入力用 ABC =101 000から101 の範囲 。他の可能な入力（ 110、111）の出力が何であるかは関係ありません 。気にしないようにこれら2つをマップします。 2つの解決策を示します。

右側のOut =AB’Cのソリューションは、ドントケアセルを使用しなかったため、より複雑なソリューションです。真ん中のソリューションであるOut =ACは、ドントケアセルを単一の 1 でグループ化したため、それほど複雑ではありません。 2つのグループを形成します。

3番目の解決策である右側のProduct-Of-Sumsは、3つのゼロでドントケアをグループ化して4つの 0 のグループを形成した結果です。 s。これは同じですが、それほど複雑ではありません。 Out =AC 。

ドントケアセルは 1 のいずれかとして使用できることを示しました sまたは 0 s、どちらか便利な方。

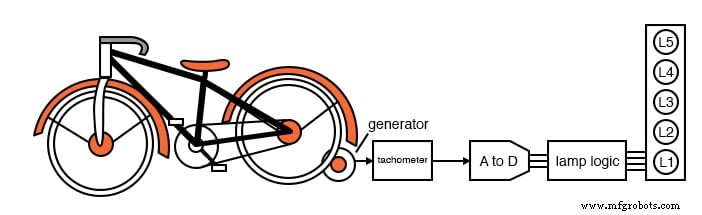
ライトニングステートカレッジの電子機器クラスは、地元の科学博物館でのエアロバイク展示用のランプロジックの構築を依頼されました。ライダーがペダリング速度を上げると、棒グラフ表示でランプが点灯します。

ランプは動きがないために点灯しません。速度が上がると、下のランプ、L1が点灯し、次にL1とL2が点灯し、次にL1、L2、L3が点灯し、すべてのランプが最高速度で点灯します。すべてのランプが点灯すると、それ以上速度を上げてもディスプレイに影響はありません。

自転車のタイヤに接続された小さなDC発電機は、速度に比例した電圧を出力します。これは、すべてのランプが点灯する最高速度で電圧を制限するタコメータボードを駆動します。これ以上速度を上げても、このレベルを超えて電圧を上げることはできません。

ダウンストリームのA-D（アナログ-デジタル）コンバーターは3ビットコード ABC を出力するため、これは非常に重要です。 、2 ³ または8コードですが、ランプは5つしかありません。 A 最上位ビット、 C 最下位ビット。

ランプロジックは、AからDまでの6つのコードに応答する必要があります。 ABC =000 の場合 、動きなし、ランプなし。 5つのコードの場合（001から101） ランプL1、L1＆L2、L1＆L2＆L3、速度、電圧、およびA to Dコード（ABC）が増加すると、最大すべてのランプが点灯します。

入力コードへの応答は気にしません（110、111） タコメータブロックの制限により、これらのコードがAからDに出ることはありません。 5つのランプを駆動するために5つの論理回路を設計する必要があります。

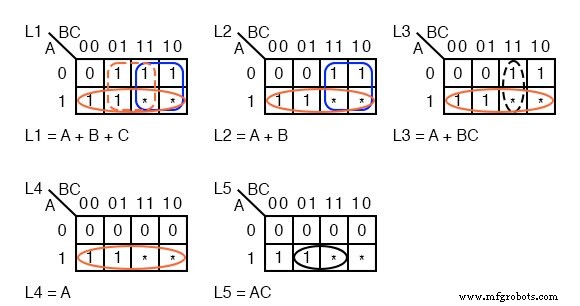
以来、 ABC =000 のランプはどれも点灯しません AからDから、 0 を入力します セル ABC =000 のすべてのKマップ 。遭遇することのないコードは気にしないので（110、111） 、5つのKマップすべての2つのセルにアスタリスクを入力します。

ランプL5は、コード ABC =101 の場合にのみ点灯します 。 1 を入力します そのセルと5つの 0 s L5K-mapの残りの空のセルに入れます。

L4は、コード ABC =100 で最初に点灯します 、 ABC =101 より大きいコードについては、点灯したままになります 、L5が点灯すると、L5より下のすべてのランプが点灯するためです。 1 と入力します sセルに 100 および 101 それらのコードのためにそれが点灯するようにL4マップの。 4つの 0 残りのL4セルを埋めます

L3は、コード ABC =011 に対して最初に点灯します 。また、L5とL4が点灯するたびに点灯します。 3つの 1 を入力します sセルに 011、100、101 L3マップ用。 3つの 0 を入力します s残りのL3セルに入れます。

ABC =010 のL2ライト とコードが大きい。 1 に入力します sセルに 010、011、100、101 、および2つの 0 残りのセルにあります。

L1が点灯しないのは、動きがない場合のみです。すでに 0 があります セル内 ABC =000 。他の5つのセルはすべて 1 を受け取ります s。

1 をグループ化します 上に示したように、より大きなグループが結果として生じる場合は常に、do n’tcareを使用します。 L1マップは、4セルの3つのグループに対応する3つの積項を示しています。

2つのグループではドントケアを使用し、3番目のグループでは1つのドントケアを使用しました。ドントケアにより、4人のグループを形成することができました。

同様に、L2マップとL4マップはどちらも、ドントケアセルを使用して4セルのグループを生成します。 L4ランプは、A / Dコンバータの最上位ビット、 L5 =A によって制御されるという点で、L4の削減は目を見張るものがあります。 。

ランプL4には論理ゲートは必要ありません。 L3およびL5マップでは、単一のセルは、ドントケアセルを持つ2つのグループを形成します。 5つのマップすべてで、縮小されたブール方程式は、ドントケアがない場合よりも複雑ではありません。

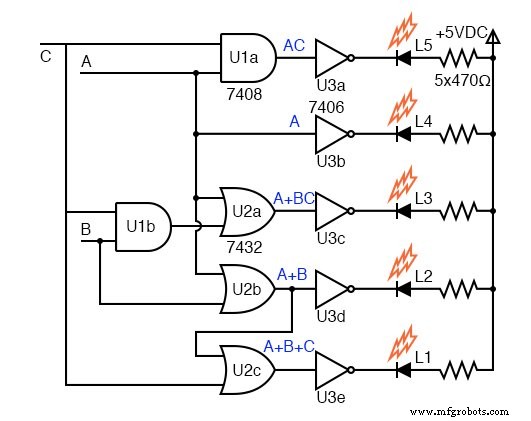
回路のゲート図は上にあります。 5つのKマップ方程式の出力はインバーターを駆動します。 L1 またはに注意してください ゲートは3入力ゲートではなく、入力（A + B）、C を持つ2入力ゲートです。 、 A + B + C を出力 オープンコレクター インバーター、 7406 、LEDの駆動には望ましいですが、K-mapロジック設計の一部ではありません。

オープンコレクタゲートまたはインバータの出力は、集積回路パッケージの内部のコレクタで開回路になっているため、すべてのコレクタ電流が外部負荷を流れる可能性があります。いずれかのインバーターにアクティブハイが入ると、出力がローになり、LEDと電流制限抵抗に電流が流れます。

LEDは、美術館の展示用に120 VACランプを駆動するソリッドステートリレーの一部である可能性がありますが、ここには示されていません。

関連するワークシート：

• デジタルディスプレイ回路ワークシート
• カルノーマッピングワークシート