方形波信号

任意 繰り返される非正弦波は、さまざまな振幅と周波数でのDC電圧、正弦波、および/または正弦波（90度の位相シフトを持つ正弦波）の組み合わせと見なすことができます。

これは、問題の波形がどれほど奇妙で複雑であっても当てはまります。時間の経過とともに定期的に繰り返される限り、この一連の正弦波に還元できます。

特に、方形波は、同じ周波数の正弦波と、振幅が減少する無限の一連の奇数多重周波数の正弦波の合計と数学的に同等であることがわかっています。

波形についてのこの真実は、最初は信じられないほど奇妙に思えるかもしれません。ただし、方形波が実際に加算された無限の一連の正弦波高調波である場合、いくつかの正弦波高調波を加算して方形波の近似値を生成することにより、これを証明できるはずです。

>

この推論は健全であるだけでなく、SPICEで簡単に実証できます。

シミュレートする回路は、適切な振幅と周波数が直列に接続されたいくつかの正弦波AC電圧源にすぎません。 SPICEを使用して、次のように、電圧源を連続して追加したときの電圧波形をプロットします。

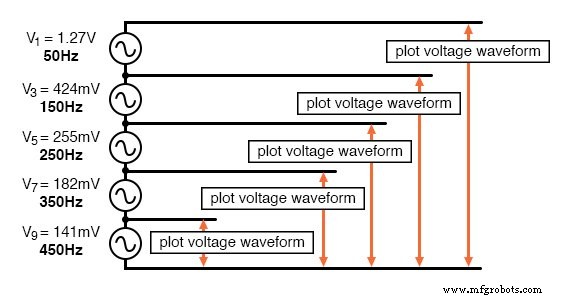
方形波は高調波の合計で近似されます。

この特定のSPICEシミュレーションでは、1番目、3番目、5番目、7番目、および9番目の高調波電圧源を直列に合計して合計5つのAC電圧源にしました。基本周波数は50Hzで、各高調波はもちろんその周波数の整数倍です。

振幅（電圧）の数値は乱数ではありません。むしろ、それらは周波数系列に示されている方程式（増加する奇数次高調波のそれぞれについて、分数4 /πに1、1 / 3、1 / 5、1 / 7などを掛けたもの）によって得られました。

方形波の構築 v1 1 0 sin（0 1.27324 50 0 0）第1高調波（50 Hz） v3 2 1 sin（0 424.413m 150 0 0）第3高調波 v5 3 2 sin（0 254.648m 250 0 0）第5高調波 v7 4 3 sin（0 181.891m 350 0 0）第7高調波 v9 5 4 sin（0 141.471m 450 0 0）第9高調波 r1 5 0 10k .tran 1m 20m .plot tran v（1,0）第1高調波をプロット .plot tran v（2,0）1次+3次高調波をプロット .plot tran v（3,0）1次+3次+5次高調波をプロット .plot tran v（4,0）1次+3次+5次+7次高調波をプロット .plot tran v（5,0）1番目のプロット+。 。 。 +9次高調波 。終わり 

ここから分析を段階的に説明し、私たちが何を見ているのかを説明します。この最初のプロットでは、50Hzの基本周波数の正弦波自体が見られます。これは純粋な正弦波に過ぎず、追加の高調波成分はありません。これは、理想的なAC電源によって生成される種類の波形です：

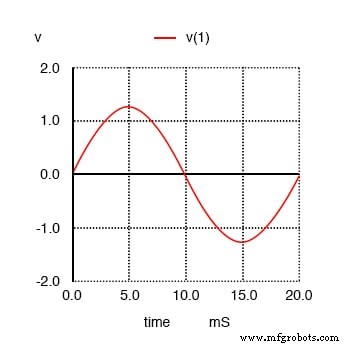
純粋な50Hzの正弦波。

次に、このクリーンでシンプルな波形を3次高調波（50Hzまたは150Hzの3倍）と組み合わせるとどうなるかを確認します。突然、それはもはやきれいな正弦波のようには見えなくなります：

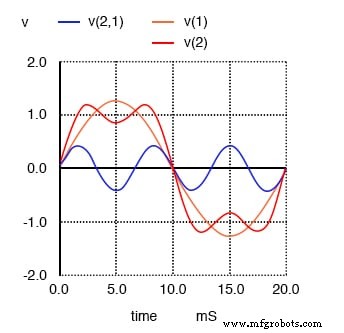
1次（50 Hz）と3次（150 Hz）の高調波の合計は、50Hzの方形波に近似します。

現在、正と負のサイクル間の立ち上がり時間と立ち下がり時間ははるかに急であり、波の頂上は方形波のように平坦に近づいています。次の奇数次高調波周波数を追加するとどうなるかを見てください：

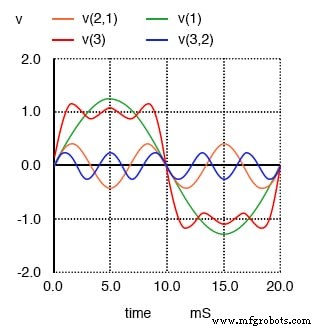
1次、3次、5次高調波の合計は、方形波に近似します。

ここで最も顕著な変化は、波の頂上がさらに平らになったことです。波の両端にはさらにいくつかのディップとクレストがありますが、それらのディップとクレストの振幅は以前よりも小さくなっています。次の奇数倍音波形をミックスに追加するときにもう一度見てください：

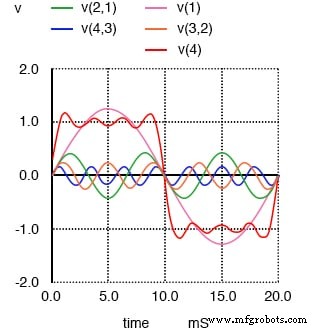
1次、3次、5次、7次の高調波の合計は、方形波に近似します。

ここでは、波が各ピークでより平坦になるのを見ることができます。最後に、回路に5番目の正弦波電圧源である9次高調波を追加すると、次の結果が得られます。

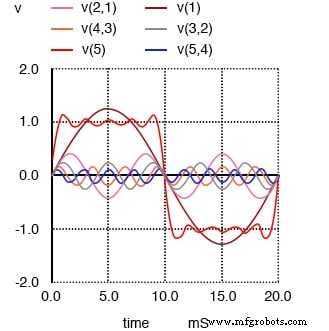
1次、3次、5次、7次、9次の高調波の合計は方形波に近似します。

最初の5つの奇数次高調波波形を（もちろんすべて適切な振幅で）加算した最終結果は、方形波の近似値です。これを行う際のポイントは、異なる周波数の複数の正弦波から方形波を構築する方法を説明し、純粋な方形波が実際にシリーズと同等であることを証明することです。 正弦波の。

方形波AC電圧が無効成分（コンデンサとインダクタ）を含む回路に印加されると、それらの成分は、実際には異なる周波数のいくつかの正弦波電圧にさらされているかのように反応します。

繰り返される非正弦波が明確な一連の付加的なDC電圧、正弦波、および/または余弦波と同等であるという事実は、波がどのように機能するかの結果です。電気的またはその他のすべての波関連現象の基本的な特性です。

非正弦波をこれらの構成周波数に還元する数学的プロセスは、フーリエ解析と呼ばれます。 、その詳細はこのテキストの範囲をはるかに超えています。ただし、実際の波形でこの分析を高速で実行するためにコンピュータアルゴリズムが作成されており、AC電力品質および信号分析への応用が広まっています。

SPICEには、波形をサンプリングし、フーリエ変換を使用して、波形を構成する正弦波の高調波に変換する機能があります。 アルゴリズム、周波数分析を数値の表として出力します。これを方形波で試してみましょう。これは、奇数次高調波の正弦波で構成されていることがすでにわかっています。

方形波分析ネットリスト v1 1 0パルス（-1 1 0 .1m .1m 10m 20m） r1 1 0 10k .tran 1m 40m .plot tran v（1,0） .four 50 v（1,0） 。終わり 

パルス 電圧源 v1 を説明するネットリスト行のオプション SPICEに、正方形の「パルス」波形をシミュレートするように指示します。この場合は、対称で（各半サイクルに等しい時間）、ピーク振幅が1ボルトです。まず、分析する方形波をプロットします。

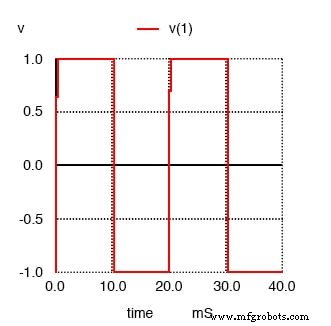
SPICEフーリエ解析用の方形波

次に、この方形波に対してSPICEによって生成されたフーリエ解析を印刷します。

過渡応答のフーリエ成分v（1） DCコンポーネント=-2.439E-02 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 5.000E + 01 1.274E + 00 1.000000 -2.195 0.000 2 1.000E + 02 4.892E-02 0.038415 -94.390 -92.195 3 1.500E + 02 4.253E-01 0.333987 -6.585 -4.390 4 2.000E + 02 4.936E-02 0.038757 -98.780 -96.585 5 2.500E + 02 2.562E-01 0.201179 -10.976 -8.780 6 3.000E + 02 5.010E-02 0.039337 -103.171 -100.976 7 3.500E + 02 1.841E-01 0.144549 -15.366 -13.171 8 4.000E + 02 5.116E-02 0.040175 -107.561 -105.366 9 4.500E + 02 1.443E-01 0.113316 -19.756 -17.561 全高調波歪み=43.805747パーセント 

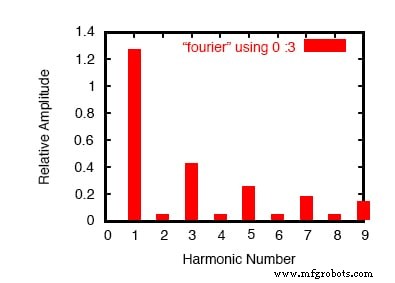
フーリエ解析結果のプロット。

ここで、（上の図）SPICEは、波形を9次高調波までの正弦波周波数のスペクトルと、 DC成分というラベルの付いた小さなDC電圧に分解しました。 。

基本周波数（20ミリ秒周期の方形波の場合、この周波数は50 Hz）をSPICEに通知する必要があったため、高調波を分類する方法を知っていました。すべての偶数次高調波（2次、4次、6次、8次）の数値がどれほど小さいか、および奇数次高調波の振幅がどのように減少するか（1次が最大、9次が最小）に注意してください。

この「フーリエ変換」の同じ手法は、コンピュータ化された電力計装でよく使用され、AC波形をサンプリングし、その高調波成分を決定します。このための一般的なコンピュータアルゴリズム（タスクを実行するための一連のプログラムステップ）は、高速フーリエ変換です。 または FFT 機能。

これらのコンピュータルーチンがどのように機能するかを正確に気にする必要はありませんが、それらの存在とアプリケーションに注意してください。

波の倍音成分を分析するためにSPICEで使用されているのと同じ数学的手法を、音楽のテクニカル分析に適用できます。つまり、特定の音を構成する正弦波周波数に分解します。

実際、それが何であるかを理解せずにまさにそれを行うように設計されたデバイスを見たことがあるかもしれません！ グラフィックイコライザー は、音楽のハーモニックコンテンツの性質を制御する（場合によっては表示する）ハイファイステレオ機器です。

イコライザーは、いくつかのノブまたはスライドレバーを備えており、音楽に存在する特定の周波数の振幅を選択的に減衰（低減）して、リスナーの利益のためにサウンドを「カスタマイズ」することができます。通常、各コントロールレバーの横に「棒グラフ」が表示され、特定の各周波数の振幅が表示されます。

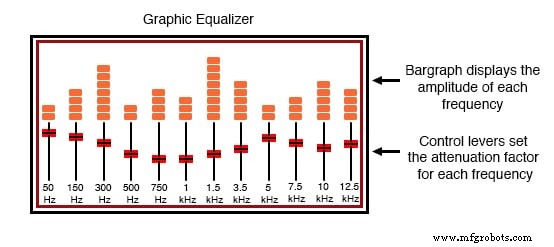
Hi-Fiオーディオグラフィックイコライザー。

混合周波数信号の各周波数範囲の振幅を制御ではなく表示するために厳密に構築されたデバイスは、通常、スペクトラムアナライザと呼ばれます。 。

スペクトラムアナライザの設計は、異なる周波数を互いに分離するように設計された一連の「フィルタ」回路（詳細は次の章を参照）のように単純な場合もあれば、FFTアルゴリズムを実行する専用デジタルコンピュータのように複雑な場合もあります。信号を数学的にその高調波成分に分割します。

スペクトラムアナライザは、無線送信機やコンピュータネットワークハードウェアによって生成される信号など、非常に高い周波数の信号を分析するように設計されていることがよくあります。その形式では、多くの場合、オシロスコープのような外観になります。

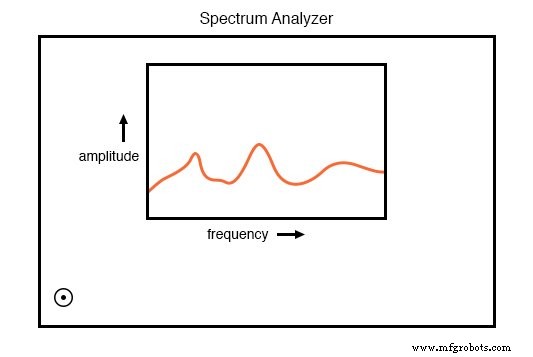
スペクトラムアナライザは、周波数の関数として振幅を表示します。

オシロスコープのように、スペクトラムアナライザはCRT（またはCRTを模倣したコンピュータディスプレイ）を使用して信号のプロットを表示します。

オシロスコープとは異なり、このプロットは周波数にわたる振幅です。 時間の振幅ではなく 。本質的に、周波数アナライザーは、オペレーターに信号のボード線図を提供します。エンジニアが周波数領域と呼ぶものです。 時間領域ではなく 分析。

「ドメイン」という用語は数学的なものです。グラフの横軸を表す洗練された言葉です。したがって、オシロスコープの時間（水平）に対する振幅（垂直）のプロットは「時間領域」分析であり、スペクトラムアナライザの周波数（水平）に対する振幅（垂直）のプロットは「周波数領域」分析です。

SPICEを使用して、ある範囲の周波数にわたって信号振幅（電圧または電流振幅のいずれか）をプロットする場合、周波数領域を実行します。 分析。

前回のSPICEシミュレーションのフーリエ解析が「完璧」ではないことに注意してください。理想的には、すべての偶数次高調波の振幅は完全にゼロである必要があり、DC成分も完全にゼロである必要があります。繰り返しになりますが、これは一般的な波形の特性であるため、SPICEの癖ではありません。

無限の持続時間（無限のサイクル数）の波形は絶対的な精度で分析できますが、分析に使用できるコンピューターのサイクルが少ないほど、分析の精度は低くなります。フーリエ解析が波形を明確な一連の正弦波に変換できるのは、波形全体を表す方程式がある場合のみです。

波が循環する回数が少ないほど、その周波数の確実性は低くなります。この概念を論理的に極端にすると、短いパルス（サイクルを完了しない波形）は実際には周波数がありません 、ではなく、無限の周波数範囲として機能します。この原則はすべてに共通です AC電圧と電流だけでなく、波に基づく現象。

サイクル数と波形の周波数成分の確実性は直接関係していると言えば十分です。

ここでは、波を何度も振動させることで分析の精度を向上させることができ、その結果、理想とより一致するスペクトル分析が得られます。次の分析では、簡潔にするために波形プロットを省略しました。これは非常に長い方形波です：

方形波 v1 1 0パルス（-1 1 0 .1m .1m 10m 20m） r1 1 0 10k .option limpts =1001 .tran 1m 1 .plot tran v（1,0） .four 50 v（1,0） 。終わり 過渡応答のフーリエ成分v（1） DCコンポーネント=9.999E-03 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 5.000E + 01 1.273E + 00 1.000000 -1.800 0.000 2 1.000E + 02 1.999E-02 0.015704 86.382 88.182 3 1.500E + 02 4.238E-01 0.332897 -5.400 -3.600 4 2.000E + 02 1.997E-02 0.015688 82.764 84.564 5 2.500E + 02 2.536E-01 0.199215 -9.000 -7.200 6 3.000E + 02 1.994E-02 0.015663 79.146 80.946 7 3.500E + 02 1.804E-01 0.141737 -12.600 -10.800 8 4.000E + 02 1.989E-02 0.015627 75.529 77.329 9 4.500E + 02 1.396E-01 0.109662 -16.199 -14.399 

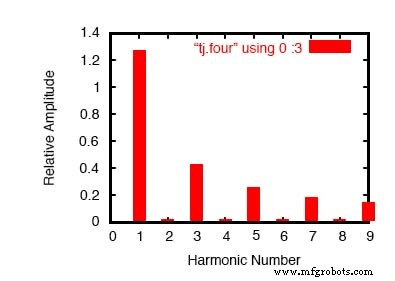
フーリエ解析を改善しました。

この分析（上の図）では、偶数次高調波周波数の正弦波のそれぞれについて、DC成分の電圧が低く、振幅が小さいことが示されています。これはすべて、コンピューターに波のサイクルをより多くサンプリングさせるためです。繰り返しになりますが、最初の分析の不正確さは、波と信号分析の基本的な特性であるため、SPICEの欠陥ではありません。

レビュー：

• 方形波は、同じ（基本）周波数の正弦波に、振幅が減少する奇数倍の正弦波高調波の無限の系列に追加されたものと同等です。
• 波形をサンプリングし、その構成要素である正弦波成分を決定できるコンピューターアルゴリズムが存在します。 フーリエ変換 アルゴリズム（特に高速フーリエ変換 、または FFT ）は、SPICEなどのコンピュータ回路シミュレーションプログラムや、電力品質を判断するための電子計測機器で一般的に使用されています。

関連するワークシート：

• 方形波信号ワークシート