異なる回転角のエンクロージャー内のTiO2-水ナノ流体の安定性と自然対流に関する実験的研究

背景

ナノ流体が調製されるため、その優れた熱伝導特性[1,2,3]により、ナノ流体は熱伝達分野[4,5,6]、特に自然対流分野[7,8,9]に広く適用されます。

ナノ流体の自然対流熱伝達特性は、多くの研究者によって数値的に調査されています。彼等。 [10、11]は、単相および二相格子ボルツマン法を適用して、Al ₂ の自然対流熱伝達を数値的に研究しました。 O ₃ -それぞれ正方形の空洞内の水ナノ流体。 Sheikholeslami etal。 [12]は、Al ₂ で満たされた内側の三角円筒を備えた水平円筒エンクロージャの電磁流体力学的自然対流熱伝達特性を調査しました。 O ₃ -格子ボルツマンシミュレーション法による水ナノ流体。 Uddin etal。 [13]は、Darcy-Forchheimerモデルに基づいて、多孔質媒体に埋め込まれた垂直プレートに沿ったさまざまなナノ流体の自然対流熱伝達を研究しました。 Meng etal。 [14] Al ₂ で満たされた水平シリンダーの自然対流を数値的に調査しました O ₃ -水ナノ流体。 Ahmed etal。 [15]は、二相格子ボルツマン法を使用して、傾斜したエンクロージャー内のCuO-水ナノ流体の自然対流を研究しました。 Qi etal。 [16]エンクロージャー内のCu-Gaナノ流体の自然対流を数値的にシミュレートしました。

ナノ流体の自然対流に関する上記の数値シミュレーションに加えて、ナノ流体の自然対流に関する実験的研究は、ますます多くの研究者によって行われています。 Li etal。 [17] ZnO-EG /水ナノ流体の自然対流熱伝達を実験的に調査しました。 Hu etal。 [18、19]は、TiO ₂ で満たされた正方形のエンクロージャの自然対流熱伝達の向上を実験的に研究しました。 -水とAl ₂ O ₃ -それぞれ水ナノ流体。 Ho etal。 [20]は、Al ₂ で満たされたさまざまなサイズの垂直正方形エンクロージャーの自然対流熱伝達を実験的に研究しました。 O ₃ -水ナノ流体。ヘリスら。 [21,22,23]は、さまざまな種類のナノ流体（Cu /水、Al ₂ ）の対流熱伝達特性を実験的に調査しました。 O ₃ -それぞれ、円形チューブ内の水、およびCuO-水）。 Mansour etal。 [24] Al ₂ で満たされた傾斜管の混合対流を実験的に調査しました O ₃ -水ナノ流体。 Chang etal。 [25] Al ₂ の自然対流を実験的に調査しました O ₃ -薄いエンクロージャー内の水ナノ流体。ウェンら。 [26、27]は、Al ₂ の対流熱伝達特性を実験的に調査しました。 O ₃ -水ナノ流体とTiO ₂ -それぞれ層流条件下の水ナノ流体。 Xuan etal。 [28]真っ直ぐな真ちゅう管内のCu-水ナノ流体の対流熱伝達を実験的に研究しました。

上記の文献は、ナノ流体の自然対流熱伝達特性に大きく貢献しました。ただし、ナノ流体で満たされた異なる回転角を持つエンクロージャの自然対流熱伝達の強化は、さらに調査する必要があります。したがって、TiO ₂ の安定性と自然対流熱伝達特性 -回転角が異なるエンクロージャー内の水ナノ流体（α =−45°、α =0°、α =45°、およびα =90°）は、この論文で実験的に調査されています。

メソッド

ナノ流体の調製とその安定性

TiO ₂ ナノ粒子として選択されます。図1は、TiO ₂ のSEM、TEM、およびXRD画像を示しています。 異なる倍率でのナノ粒子。 SEM画像からナノ粒子が容易に集まることがわかり、安定したナノ流体を調製するためにいくつかの対策を講じる必要があります。また、TEM画像から粒子サイズは約10 nmであり、ナノ粒子の形状は平坦であることがわかります。平らなナノ粒子は、同じ質量分率で球状のナノ粒子よりも大きな熱伝達面積を持っており、これは熱伝達の向上に有利です。図1gは、TTP-A10 TiO ₂ のXRDパターンを示しています。 ナノ粒子。観察されたように、強くて鋭いピークは、TTP-A10 TiO ₂ ナノ粒子サンプルは結晶性が高いです。サンプルの平均粒子サイズは、式（1）に示されているシェラーの式によって計算できます。 （1）。 TiO ₂ ナノ粒子のサイズは、これらの回折ピーク値（111、200、021、202、および311）によって計算された6、9、14、20、および35 nmであり、最小のナノ粒子サイズは、回折ピーク値に基づいて約6および9nmです。 （111および200）。大きなナノ粒子サイズは、ナノ粒子の凝集によって引き起こされる可能性があります。最小値（6および9 nm）はナノ粒子の実際のサイズであり、いくつかのナノ粒子のサイズは6 nmであり、ほとんどのナノ粒子のサイズは約9 nmであり、製造元から提供された説明にさらに近いです（ 10 nm）およびTEM画像（10 nm）。

ここで k は形状係数の値であり、 k =0.9; λ X線の波長です。およびβ は、ラジアン単位のピーク高さの半値全幅（FWHM）を広げる線であり、θ はブラッグ回折角です。

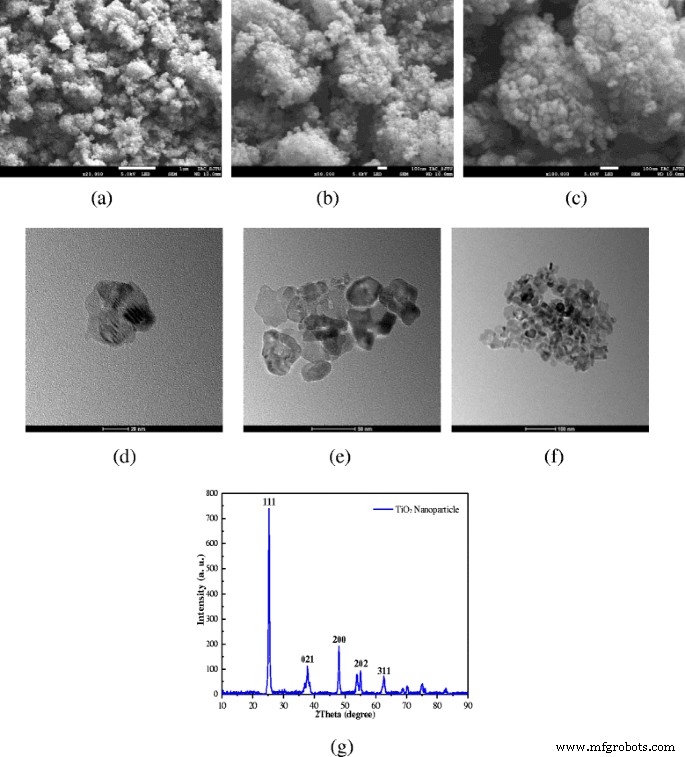
ナノ粒子の形態。 TiO ₂ のSEM、TEM、およびXRD画像 異なる倍率でのナノ粒子。 a SEM×20000。 b SEM×50000。 c SEM×100000。 d TEM 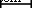20 nm e TEM 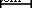50 nm f TEM 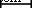100 nm g XRD

TiO ₂ -ナノ粒子の質量分率が異なる水ナノ流体（wt％=0.1％、wt％=0.3％、wt％=0.5％）は、図2に示す2段階の方法で調製されます。機械的攪拌時間は半分です。各サブステップで1時間、超音波処理時間は40分です。表1は、ナノ流体の調製におけるいくつかの材料と装置の情報を示しています。図3は、TiO ₂ を示しています。 -敷設前および72時間後の水ナノ流体。試験管内のナノ粒子の堆積はほとんどなく、この論文で調製されたナノ流体は良好な安定性を示していることがわかります。

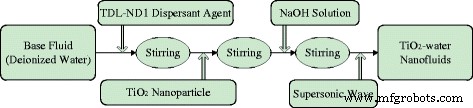
ナノ流体の調製。 TiO ₂ の準備手順 -2段階法による水ナノ流体

TiO ₂ の安定性の観察 -水ナノ流体。 TiO ₂ -異なる時間の水ナノ流体。 a 敷設する前に。 b 72時間後

試験管内にナノ粒子が堆積しているかどうかの研究に加えて、透過率の影響（τ ）その安定性に関するナノ流体についても説明します。図4に透過率（τ）を示します。 ）TiO ₂ の変更 -さまざまなpH値と用量（ m ）の水ナノ流体（wt％=0.5％） ）分散剤の。透過率は、紫外可視分光光度計（UV-1800（PC））で測定します。ご存知のように、ナノ粒子が水中に均一に分布している場合、ナノ粒子は最も多くの光を反射し、高い反射率（低い透過率）を持ちます。したがって、ナノ流体の安定性は透過率に反比例し、安定したナノ流体の透過率は低くなります。図4から、 m のナノ流体であることがわかります。 =6 wt％およびpH =8は透過率が最も低く、安定性が最も高くなります。この実験でのナノ粒子の質量分率が異なるナノ流体は、 m で調製されます。 =6 wt％およびpH =8、これによりナノ流体の安定性を確保できます。

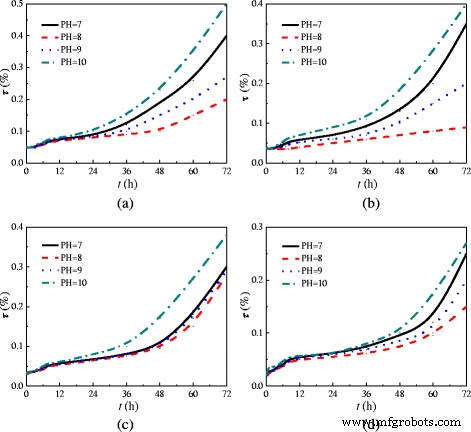
TiO ₂ の透過率 -水ナノ流体。透過率（τ ）TiO ₂ の変更 -時間（ h ）の異なるpH値での水ナノ流体（wt％=0.5％） ）異なる用量で（ m ）分散剤の。 a m =5 wt％。 b m =6 wt％。 c m =7 wt％。 d m =8 wt％

実験システム

図5に、3つの実験セットの概略図を示します。 3つの長方形のエンクロージャーのサイズは、10cm（幅）×20cm（高さ）、5cm（幅）×20cm（高さ）、および20cm（幅）×20cm（高さ）です。幅と高さは W として定義されます および H 、それぞれ、アスペクト比（ A ）エンクロージャの）は A =W / H として定義されます 。エンクロージャーの左側の壁（銅板）は、DC電源に接続されたシリコン加熱シートによって加熱されます。エンクロージャーの右側の壁（銅板）は、恒温水槽に接続された小さな空洞（材料も銅）内の冷却水によって冷却されます。エンクロージャの両側の温度は、データ取得機器（Agilent 34972A）に接続された6つの熱電対によって取得されます。外側の断熱層は、熱の損失を防ぐために使用されます。

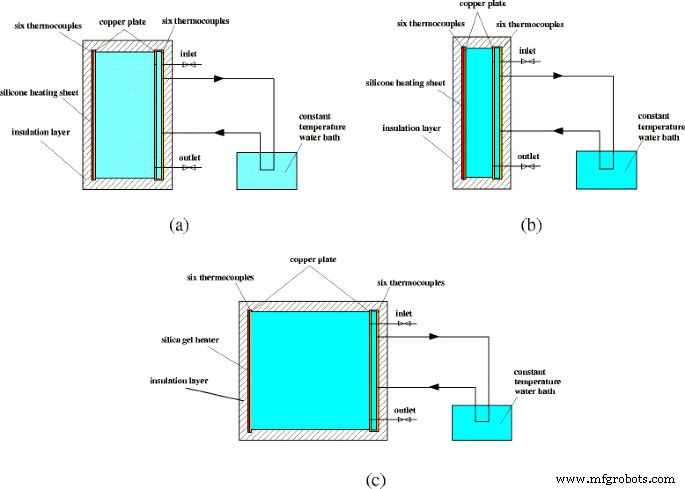
実験セットの概略図。 3つの異なるアスペクト比の実験セットの概略図。 a A =1：2。 b A =1：4。 c A =1：1

回転角（α）が異なる2つのエンクロージャーの自然対流熱伝達特性 =−45°、α =0°、α =45°、およびα =90°）TiO ₂ で満たされています -水ナノ流体は、この論文で調査されます。 αのエンクロージャーの場合 =−90°、上壁は高温壁、下部壁は低温壁であり、エンクロージャー内の熱伝達は主に熱伝導です。ただし、原稿は主にエンクロージャー内のナノ流体の自然対流熱伝達を調査しているため、αのエンクロージャーを使用します。 =−90°はこの原稿では考慮されていません。図6に、さまざまな回転角度のエンクロージャーの概略図を示します。

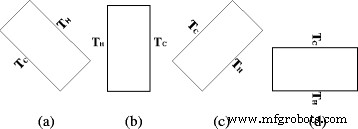
回転角の概略図。 4つの異なる回転角を持つエンクロージャーの概略図。 a α=−45°。 b α=0°。 c α=45°。 d α=90°

データ処理

パワー Q シリコーン加熱シートによって提供されるものは次のとおりです：

ここで U および私 はそれぞれDC電源の電圧と電気です。

実効電力 Q _net は次のとおりです：

ここで Q _損失 は、熱流量計によって測定された熱損失です。

シリコン加熱シートの隣の銅板側の温度\（{T} _ {\ mathrm {H}} ^ {*} \）は次のとおりです。

ここで T ₁ 、 T ₂ 、…、 T ₆ は熱電対の温度です。

ナノ流体 T の隣の銅板側（エンクロージャーの左側）の温度 _H は次のとおりです：

ここで、δ =0.005mは銅板の厚さ、 A は銅板の面積、λ _w は銅板の熱伝導率です。

絶縁層の隣の銅板側（エンクロージャーの右側）の温度 T _C ^∗ は次のとおりです：

ここで T ₇ 、 T ₈ 、…、 T ₁₂ エンクロージャーの右側にある熱電対の温度です。

熱平衡状態に達すると、冷却水の温度は、冷却水の隣の銅板側の温度と同じになります。ナノ流体 T の隣の銅板側（エンクロージャーの右側）の温度 _C 次のように計算できます：

定性的温度 T _m は次のように定義されます：

対流熱伝達係数 h は次のとおりです：

ヌセルト数は次のように定義されます：

ここで、λ _f はエンクロージャー内の流体の熱伝導率です。

不確実性分析

対流熱伝達係数の誤差伝達式は次のとおりです[19]：

ヌセルト数の誤差伝達式は次のとおりです[19]：

式に基づく。 （10）と（11）の場合、この実験では、対流熱伝達係数とヌセルト数の誤差はそれぞれ5.65％と6.34％です。実験セットの誤差が小さいことがわかり、実験結果の信頼性と精度を確保できます。

結果と考察

実験の検証

ナノ流体の研究の前に、実験の検証が必要です。図7は、水の実験結果と A を備えたエンクロージャーに関する公開された文献の結果との間のヌセルト数の比較を示しています。 =1：2、 A =1：4、および A =1：1。 A のエンクロージャーの最大エラー =1：2、 A =1：4、および A =1：1はそれぞれ8.4、9.5、8.1％です。実験結果は、公開された文献[20、29]の結果とよく一致しており、実験システムの精度と信頼性を検証していることがわかります。

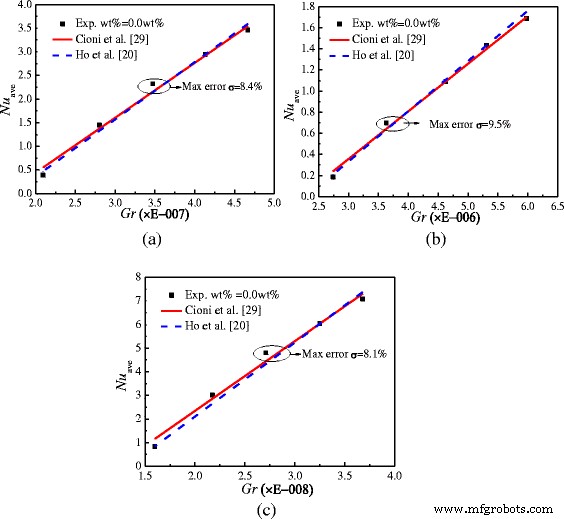
実験セットの検証。実験結果と2つの異なるアスペクト比のエンクロージャー内の公開された文献との間のヌセルト数の比較。 a A =1：2。 b A =1：4。 c A =1：1

A を使用したエンクロージャ =1：2

TiO ₂ の自然対流熱伝達特性に対する回転角の影響 -この論文では、水ナノ流体について説明します。図8は、 A を使用したエンクロージャーの回転角による平均ヌセルト数の変化を示しています。 =1：2。図8から、ヌセルト数は回転角とともに最初に増加し、次に減少することがわかります。回転角αのエンクロージャー =0°が最も高いヌセルト数を持ち、次に回転角αのエンクロージャーが続きます。 =45°およびα =90°、回転角αのエンクロージャー =−45°のヌセルト数が最も低くなります。回転角が小さくなると、熱伝導がますます重要になります（α ≤−90°）、回転角がαに減少すると、熱伝達はほぼ熱伝導になります。 =−90°。ホットウォールがエンクロージャーの上部にあり、コールドウォールがエンクロージャーの下部にある場合（α =−90°）、浮力の方向は上向きですが、上壁は流体が上向きに移動するのを防ぎます。エンクロージャー内のナノ流体の動きは小さく、主な熱伝達は熱伝導であるため、ヌセルト数が少なくなります。 αのエンクロージャ =−45°はαのエンクロージャーにより近くなります =−90°であり、他の回転角と比較して最小のヌセルト数を示します。回転角がαのエンクロージャーの場合 =45°およびα =90°、下部の高温壁の近くの流体は加熱されて上向きに移動し、上部の低温壁の近くの流体は冷却されて下向きに移動します。高温流体と低温流体の方向は反対であり、自然対流熱伝達を防ぎます。これにより、αのエンクロージャーと比較してヌセルト数が低くなります。 =0°ですが、αのエンクロージャーと比較してヌセルト数が高くなっています =−45°。また、加熱力に応じて回転角の差が大きくなることがわかります。これは、回転角の影響が低暖房電力での熱伝達に主な役割を果たし、対流の熱伝達への影響が小さいためです。ただし、対流熱伝達強度は加熱力とともに増加し、高加熱力での熱伝達に主な役割を果たします。これにより、低加熱力での場合と比較して、高加熱力でのさまざまな回転角の差が大きくなります。

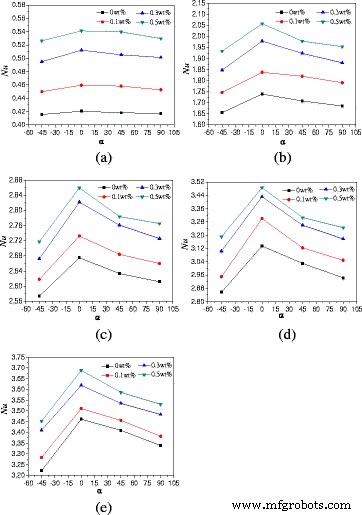
回転角によるヌセルト数の変化（ A =1：2）。エンクロージャーの回転角によるナノ流体の平均ヌセルト数の変化（ A =1：2）さまざまな加熱力で。 a Q =1W。 b Q =5W。 c Q =10W。 d Q =15W。 e Q =20W

回転角に加えて、自然対流熱伝達に対するナノ粒子の質量分率の影響についても説明します。図9は、ナノ粒子の質量分率による平均ヌセルト数の変化を示しています。ヌセルト数はナノ粒子の質量分率とともに増加することがわかります。暖房用 Q =1Wおよびα =0°、TiO ₂ -wt％=0.1％、wt％=0.3％、およびwt％=0.5％の水ナノ流体は、水と比較して、それぞれ9.3、21.8、および28.7％の熱伝達を向上させることができます。増強率は加熱力とともに減少します。暖房用 Q =20Wおよびα =0°、TiO ₂ -wt％=0.1％、wt％=0.3％、およびwt％=0.5％の水ナノ流体は、水と比較して、それぞれ1.4、4.6、および6.6％の熱伝達を向上させることができます。乱流強度は、高い加熱力で主要な役割を果たすようになり、熱伝達に対するナノ粒子の質量分率の影響は小さくなります。

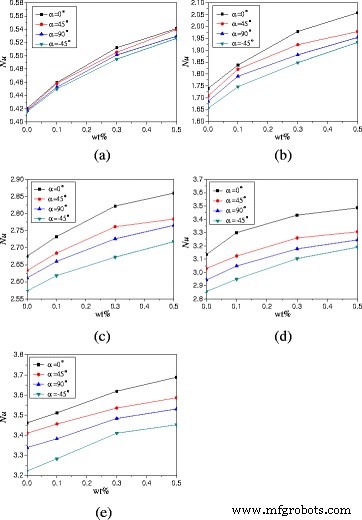
ナノ粒子の質量分率によるヌセルト数の変化（ A =1：2）。エンクロージャー内のナノ流体の平均ヌセルト数の変化（ A =1：2）さまざまな加熱力でのナノ粒子の質量分率。 a Q =1W。 b Q =5W。 c Q =10W。 d Q =15W。 e Q =20W

自然対流熱伝達に及ぼす加熱力の影響をこの論文で研究した。図10は、加熱力による平均ヌセルト数の変化を示しています。 αの場合 =0°、TiO ₂ - Q での水ナノ流体 =5 W、 Q =10 W、 Q =15 W、および Q =20 Wは、 Q と比較して、熱伝達を280.2、428.4、544.1、および581.5％向上させることができます。 =1W。高い加熱力は乱流強度を高め、熱伝達を改善します。

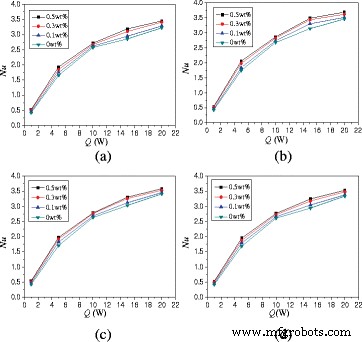
加熱力によるヌセルト数の変化（ A =1：2）。エンクロージャー内のナノ流体の平均ヌセルト数の変化（ A =1：2）さまざまな回転角度での加熱力。 a α=−45°。 b α=0°。 c α=45°。 d α=90°

A を使用したエンクロージャ =1：4

エンクロージャーのアスペクト比が熱伝達に及ぼす影響を調査するために、 A を使用したエンクロージャーの自然対流熱伝達特性 =1：4はTiO ₂ で満たされています -水ナノ流体が研究されています。図11は、エンクロージャーの回転角による平均ヌセルト数の変化を示しています。 A のような同様の結論を得ることができます =1：2ヌセルト数は最初に増加し、次に回転角とともに減少します。 wt％=0.5％の例のナノ流体の場合、 A の違い =1：4および A =1：2は、エンクロージャー（ A ）内のヌセルト数の増強率（6.5から20.7％）です。 =1：4、α =0°）エンクロージャー内のそれと比較して（ A =1：4、α =−45°）は、エンクロージャー内のヌセルト数の増強率（2.85から9.3％）よりも高くなっています（ A =1：2、α =0°）エンクロージャー内のそれと比較して（ A =1：2、α =−45°）。

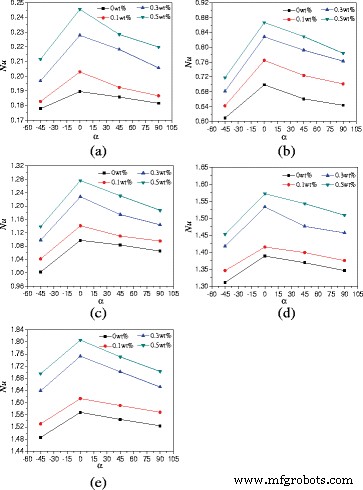
回転角によるヌセルト数の変化（ A =1：4）。エンクロージャーの回転角によるナノ流体の平均ヌセルト数の変化（ A =1：4）さまざまな加熱力で。 a Q =1W。 b Q =5W。 c Q =10W。 d Q =15W。 e Q =20W

図12は、ナノ粒子の質量分率による平均ヌセルト数の変化を示しています。暖房用 Q =1Wおよびα =0°、TiO ₂ -wt％=0.1％、wt％=0.3％、およびwt％=0.5％の水ナノ流体は、水と比較して、それぞれ7.1、20.2、および29.5％の熱伝達を向上させることができます。増強率は加熱力とともに減少します。暖房用 Q =20Wおよびα =0°、TiO ₂ -wt％=0.1％、wt％=0.3％、およびwt％=0.5％の水ナノ流体は、水と比較して、それぞれ2.9、11.8、および15.1％の熱伝達を向上させることができます。

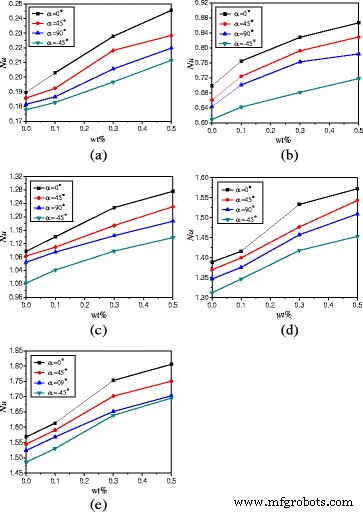
ナノ粒子の質量分率によるヌセルト数の変化（ A =1：4）。エンクロージャー内のナノ流体の平均ヌセルト数の変化（ A =1：4）さまざまな加熱力でのナノ粒子の質量分率。 a Q =1W。 b Q =5W。 c Q =10W。 d Q =15W。 e Q =20W

図13は、加熱力による平均ヌセルト数の変化を示しています。ナノ流体の平均ヌセルト数は、加熱力Q =1Wの水と比較して242.4％〜701.5％向上する可能性があります。αの場合 =0°、TiO ₂ - Q でwt％=0.5％の水ナノ流体 =5 W、 Q =10 W、 Q =15 W、および Q =20 Wは、 Q の場合と比較して、熱伝達を253.0、419.9、540.3、および635.6％向上させることができます。 =それぞれ1W。

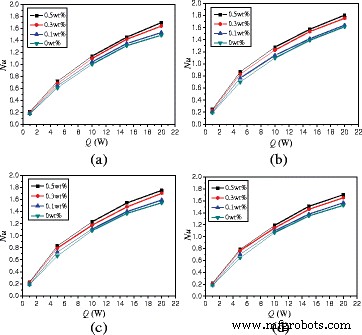
加熱力によるヌセルト数の変化（ A =1：4）。エンクロージャー内のナノ流体の平均ヌセルト数の変化（ A =1：4）さまざまな回転角度での加熱力。 a α=−45°。 b α=0°。 c α=45°。 d α=90°

A 間の比較 =1：2、 A =1：4、および A =1：1

このペーパーの長さの制限により、 A を使用したエンクロージャーの結果 =1：1は図14にのみ示され、さまざまな回転角、ナノ粒子の質量分率、および加熱力が熱伝達に及ぼす影響をすべて図14に示すことができます。 A =1：2、 A =1：4、および A =1：1、図14は、 A 間の平均ヌセルト数の比較を示しています。 =1：2、 A =1：4、および A =1：1、さまざまな回転角度で。ヌセルト数は、エンクロージャーのアスペクト比とともに増加することがわかります。エンクロージャーのヌセルト数（ A =1：1および A =1：2）は、ヌセルト数のエンクロージャー（ A ）と比較して、190.6％〜224.4％および103.6％〜172.0％向上させることができます。 =1：4）それぞれ同じ条件で。 Q の場合 =1Wおよびα =0°の例、 A のエンクロージャー内のwt％=0.5％、wt％=0.3％、wt％=0.1％、およびwt％=0.0％のナノ流体 =1：2は、 A のエンクロージャーと比較して、熱伝達を120.4、124.9、126.5、および121.9％向上させることができます。 =1：4。増強率は加熱力とともに減少します。 v Q の場合 =20Wおよびα =0°、wt％=0.5％、wt％=0.3％、wt％=0.1％、およびwt％=0.0％のナノ流体（ A のエンクロージャー内） =1：2は、A =1：4のエンクロージャーと比較して、熱伝達を104.2、106.5、117.6、120.7％向上させることができます。また、ヌセルト数がwt％=0.1％からwt％=0.3％に増加する方が、wt％=0.3％からwt％=0.5％に増加するよりも大きいことがわかります。これは、熱伝導率の増加がwt％=0.1％からwt％=0.3％への熱伝達に主な役割を果たし、大きな向上をもたらすためです。しかし、粘度の増加は、wt％=0.3％からwt％=0.5％への熱伝達において主要な役割を果たし始めます。これにより、わずかな向上が生じます。 Because Fig. 14 can cover all the experimental results, the detailed results of Fig. 14 are shown in Tables 2, 3, and 4.

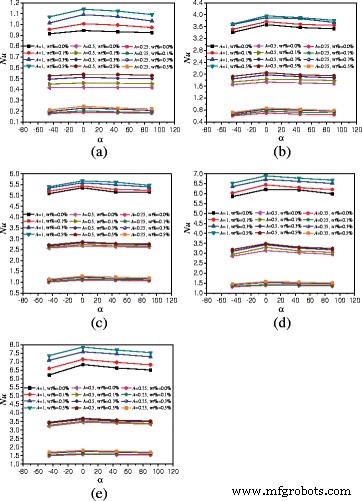
Nusselt numbers comparison between different aspect ratios. Comparison of average Nusselt numbers of nanofluid in different aspect ratios (A  = 1:1, A  = 1:2, and A = 1:4) and rotation angle enclosures at different heating powers. a Q  = 1 W. b Q  = 5 W. c Q  = 10 W. d Q  = 15 W. e Q  = 20 W

Conclusions

The stability and natural convection heat transfer characteristics of the two enclosures with different rotation angles (α  = −45°, α  = 0°, α  = 45°, and α  = 90°) filled with TiO₂ -water nanofluid are experimentally investigated. Some conclusions are obtained as follows:

1. (1)

   TiO₂ -water nanofluid with m  = 6 wt% and pH = 8 has the lowest transmittance and has the best stability.

2. (2)

   The enclosure with rotation angle α  = 0° has the highest Nusselt number followed by the enclosure with rotation angles α  = 45° and α  = 90°; the enclosure with rotation angle α  = −45° has the lowest Nusselt number.

3. (3)

   There is a higher heat transfer performance in a bigger aspect ratio enclosure. The Nusselt numbers of enclosure (A  = 1:1 and A  = 1:2) can be enhanced by 190.6% ~ 224.4% and 103.6% ~ 172.0% compared with the Nusselt numbers of enclosure (A  = 1:4) at the same conditions.

4. (4)

   Nusselt numbers increase with nanoparticle mass fractions, but the enhancement ratio decreases with the heating power.

5. (5)

   Average Nusselt numbers increase with the heating power. Average Nusselt numbers of nanofluid can be enhanced by 701.5% compared with water at the best.