分子動力学法によるアブレシブナノメートル切削プロセスに及ぼす衝撃方向の影響の研究

背景

最新の超精密機械加工では、材料除去技術がマイクロエレクトロニクス、マイクロメカニカル、および光学素子の製造において重要な役割を果たします。高い寸法精度と高品質の表面を備えた小型化されたデバイスの需要により、超精密プロセスが前述の分野の主要な選択肢となっています[1]。さらに、表面成分と表面下構造の変化は、ナノメートルの長さスケールです。研磨粒子流動研磨技術は、精密機械加工の多くの分野で重要な役割を果たしており、表面品質を向上させる他の非伝統的な仕上げ技術とまったく同じです。この技術は、その重要な役割のために多くの研究者を魅了してきました。 E. Uhlmannと他の研究者は、切削材料の効果に対するさまざまな処理要因の研削流体の流れを検証するために設計された実験のために、砥粒研磨セラミック表面のコンピューターシミュレーションを報告しました[2]。 Sehijpal Singhと他の研究者は、銅とアルミニウムの材料を切断するために研磨フロー研磨技術を使用しています。走査型電子顕微鏡分析から、彼らはワークピースの深い溝の表面を発見しました[3]。 G. Venkateshと他の研究者は、仕上げプロセスの複雑な表面の円錐歯車用の超音波支援砥粒研磨技術を報告しました。この手法では、従来の砥粒流よりも砥粒速度が速く、ワーク表面に衝突するため、加工効率を向上させることができます。彼らの実験的および理論的方法から、彼らはこの技術が歯車の刃の仕上げに最適な選択肢の1つであることを発見しました[4、5]。 K.カマル他流体研磨剤の粘度、せん断速度、およびクリープ時間における研磨液のレオロジー特性を研究しました[6]。ただし、ほとんどのアブレシブフロー研磨の研究はマクロレベルに基づいており、ミクロレベルに非常にまれな注意が払われています。アブレシブフロー研磨プロセスでは、媒体に浮遊している粒子が、マイクロカッティングワークピースの表面の衝撃を受けて、特定の速度で媒体に沿って流れます（図1）。

研磨切削ワークのスケッチ。すべての図は、分子動力学を使用した研磨ナノメートル切削プロセスに対する衝撃方向の影響に関するものです。図1は、研磨切削ワークのスケッチです。アブレシブフロー研磨プロセスでは、媒体に浮遊している粒子が、マイクロカッティングワークピースの表面の衝撃を受けて、特定の速度で媒体に沿って流れます

砥粒の形状は規則的ではないため、工具と同様に、ワークピースの表面に作用する特定のエッジとコーナーがあります。しかし、切断プロセスは原子スケールであり、材料除去プロセスとは明らかに異なります。ナノスケールの切断では、材料表面が数ナノメートル以下になりますが、実験でこのプロセスを観察することは非常に困難です。したがって、理論的調査方法としてのMDシミュレーションは、ナノメートル切断プロセスの研究に非常に役立ちます。コンピュータシミュレーション技術としての分子動力学。これは、時間ベースの統計力学法を使用して、条件の予測と分析のために原子の相互関係を研究します。これは、材料除去プロセスをシミュレートおよび理解するための強力なツールでもあります。文献には、精密機械加工を調査するためのツールとしてのMDに関する多くの研究があります。 OluwajobiとChenは、銅のナノスケール機械加工のMDシミュレーションに関する広範な研究を行ってきました[7]。彼らの研究では、最小切削深さ、形状、原子間ポテンシャルなど、ナノマシニングのさまざまなパラメータを調査しました[8]。さらに、MDシミュレーションの結果は、シリコンなどの脆性材料のナノメートル切断プロセスに関する多くの問題に対処するために、過去にも成功しています[9]。 Komanduri etal。 Tersoffポテンシャルを使用して、欠陥のない純粋なシリコンの単結晶をナノメートルで切断するためのMDシミュレーションを実施しました。彼らは、すくい角、切込み幅、切込み深さ、および逃げ角が材料の除去と表面生成に及ぼす影響を研究しました[10]。 Goel etal。ナノメートル切断プロセス中のSiCの延性応答の原子的側面を調査しました。彼らは、sp3-sp2の秩序-無秩序転移の存在を発見し、最終的にダイヤモンドの黒鉛化をもたらしました[11]。カイらMDを使用して、シリコンのナノスケール延性モード切断を研究しました。彼らは、工具の刃先とそのワークピース材料のせん断応力への影響を報告しました[12]。アラフィン等。シリコンウェーハのナノスケール延性モード切断における刃先半径の影響について議論しました[13]。他のさまざまな研究者も、MDシミュレーションを使用したシリコンのナノマシニングのさまざまな条件を強調しています。そこでの調査は、切削抵抗、切削深さ、温度、せん断応力、およびその他のパラメータで構成されています。ただし、この分野では十分な実験的検証が不足しています。 Qihong Fang etal。異なるスケールの異なる異種材料における転位の相互作用メカニズム、および転位と材料の靭性と破壊損傷との関係を研究しました。彼らは、分子動力学シミュレーションを使用して、単結晶、多結晶、およびナノ双晶の多結晶銅を含む3つの異なる結晶構造へのナノインデンテーションを研究します。引っかき速度の増加に伴い、激しい塑性変形と大きな切りくず体積により、引っかき力とワークピースの温度が継続的に上昇し、転位すべり、GBすべり、双晶/双晶が発生します[14、15]。

メソッド/実験

研磨剤フロー研磨実験では、通常、ワークピースはSiC研磨剤で切断されました。 SiC砥粒のモデルが確立された後、ワークピースの分子動力学シミュレーションがソフトウェアLammpsによって実行されました。角度の異なる2つのSiC砥粒切断単結晶銅のモデルを構築しました。 SiC砥粒のクラッシュカット単結晶銅のシミュレーションモデルを図2に示します。

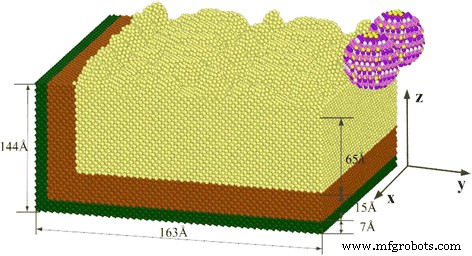
SiC砥粒切削単結晶銅のシミュレーションモデル。図2は、SiC研磨切削単結晶銅のシミュレーションモデルに関するものです。単結晶銅を切断するために2つのSiC研磨剤を作成しました。研磨剤フロー研磨実験では、通常、ワークピースはSiC研磨剤で切断されました。 SiC研磨モデルの構築後、ワークピースの分子動力学シミュレーションを実行しました。角度の異なる2つのSiC砥粒切断単結晶銅のモデルを構築しました

モデルのサイズを図2に示しますが、シミュレートされた原子の数は159,020でした。砥粒半径は15Å、砥粒中のC原子とSi原子の総数は1406であり、炭素原子とシリコン原子の数はそれぞれ681と725であった。緩和ステップ数は、シミュレートされた平衡アンサンブルに対して10,000ステップに設定され、衝突シミュレーションステップは100,000切断ステップに設定され、シミュレーションの各ステップは0.001 ps、切断シミュレーション、切断方向速度80 m / sのSiC研磨粒子でした。 AFM分析値の粒子は、研磨中にマイクロマシニングワークピースと衝突します。SiC砥粒は、分子衝突ダイナミクスのさまざまな角度の切削プロセスを調査します。アブレシブフロー切削では、切削速度が上がると切削抵抗が大きくなり、切削抵抗の大きさが切削効果に直接影響します。したがって、適切な切断速度の選択は、切断の品質に重要な影響を及ぼします。高品質の切削を実現するために、80 m / sの切削速度を選択しました。これは、ワークピースの原子間の相互作用をすばやく破壊できる切削力を生成するためです[16]。

10 m / sなどの低速切削速度での分子動力学シミュレーションでは、図1および2に示すように、原子変位マップと、炭化ケイ素研磨粒子の切削力と切削角度がシミュレーションのステップサイズによってどのように変化するかを示します。切削速度が小さすぎるため、切削力も不十分であり、格子の変形や転位がはるかに少なくなります。全体として、切削効率は低く、切削品質は比較的劣っています。対照的に、顕微鏡実験で切断速度が最大80 m / sの場合、銅原子間の化学結合を迅速かつ効果的に切断して、瞬時に高品質の切断を実現できます。したがって、包括的な分析の後、シミュレーションには80 m / sの切削速度が妥当です。

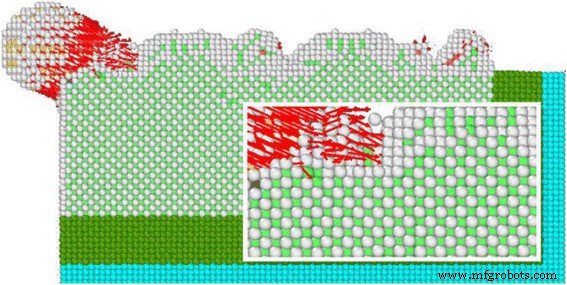
低速原子変位

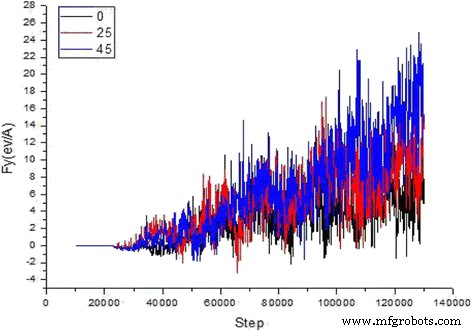
切削抵抗、切削角度、シミュレーションステップの関係

実現可能性と信頼性をシミュレートするために、原子の原子間ポテンシャルを考慮するための合理的な経験的ポテンシャル関数を選択します。さまざまな目的に応じて、ポテンシャル関数を2体ポテンシャル関数と多体ポテンシャル関数に分けることができます。単結晶銅と研磨粒子の間の2つのモデルは、モースポテンシャルによってそれらの間の原子の原子間ポテンシャルを記述し[17]、EAMポテンシャルは銅原子間の原子の原子間ポテンシャルを記述するために使用されます[18、19、20]。 SiC粒子間の相互作用は、Tersoffポテンシャル[21]を使用して記述されます。

研磨プロセス中、媒体中の砥粒の衝突方向はランダムです。それらの軌道は、ワークピースの表面に正確に沿っているわけではありません。マイクロカッティングプロセス中、砥粒のカッティング方向は必ずしもワークピースの材料に直交するとは限りません。切削角度とは、砥粒の切削方向と水平面との間の角度のことです。粒子がワークピースの表面に近づくと正になります。切削角度のスケッチを図5に示します。

切断角度のスケッチ。図5は、砥粒を切削するときのさまざまな切削角度のスケッチです。異なる方向からの砥粒がワーク材料を切断し、材料の性能と加工品質が異なります

この研究では、MDシミュレーションを使用して、切断された単結晶銅の衝撃方向が異なるマルチ研磨剤をシミュレートします。図5に示すように、銅ワークピースの表面が粗い間、切断角度は0°から45°の間です。

結果と考察

SiC研磨切削機構の衝突の分析

単結晶銅材料の切断に対する炭化ケイ素研磨剤の影響は、銅材料の単結晶の格子構造を破壊することによって達成されます。破壊中、銅原子間の相互作用、C、SiC研磨粒子のSi原子が被削材のCu原子に加えるせん断応力が切削力であることが確認されました。これは、切削力が重要な物理的パラメータであるという事実です。単結晶銅ワーク材料の除去プロセスを深く反映しています。前述のように、ミクロとマクロの切削抵抗には大きな違いがあります。一般に、マクロ切削抵抗は切削抵抗と研削力の合計ですが、マイクロ切削では、切削抵抗は砥粒とワークの原子との相互作用によって生成されます。

図6に、さまざまな方向の砥粒のせん断応力の変化、さまざまな方向のせん断応力の影響、さまざまな切削角度に沿った切削抵抗の分布を示しました。

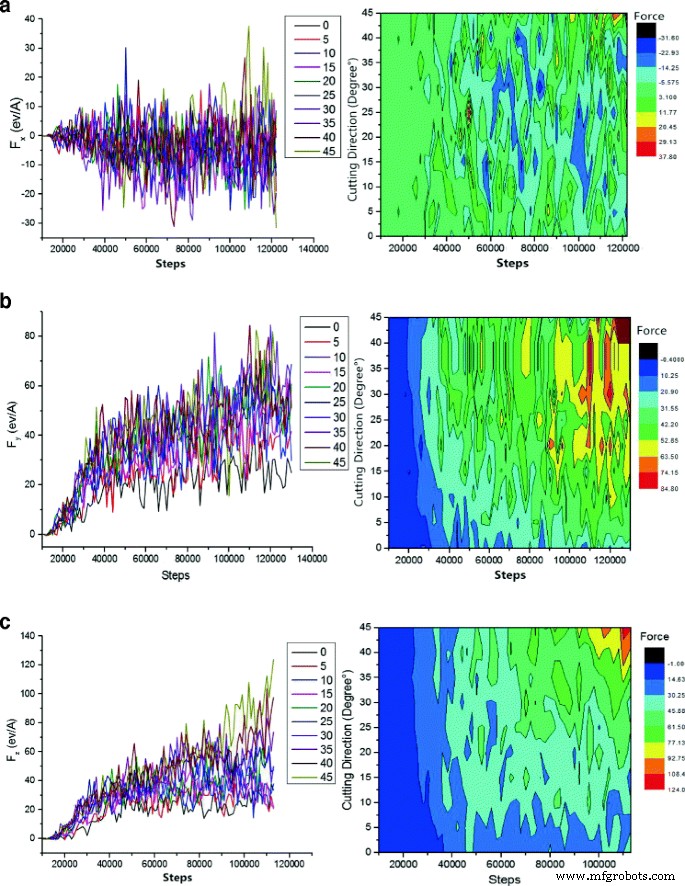
切削角度とシミュレーションステップサイズが切削抵抗にどのように影響するか。図6にSiC砥粒切削抵抗と切削角度およびシミュレーションステップ図を示します。切削深さが増すと、破壊の結晶構造の数が増え、切削抵抗の変動の最大値も大きくなります。 a [100]切削抵抗の方向。 b 【０１０】切削抵抗の方向。 c [001]切削抵抗の方向

炭化ケイ素砥粒は、[010]や[100]などのさまざまな角度のエッジで単結晶銅材料を切断して衝撃を与えます。 [001]および[010]方向に沿った切削力はせん断力でした。さらなるシミュレーションでは、切削深さが徐々に増加し、[001]および[010]方向に沿って切削抵抗が持続的に上昇しました。しかし、図6からわかるように、ある程度までこれらの力は変動しました。研磨粒子がワークピースの材料に向かって移動すると、最も外側の銅原子と原子の間の相互作用（引力から反発へ）が完全に変化しました。 SiC（SiおよびC）の。当初、被削材を研削している間、銅原子の反発力が存在するため、切削抵抗が不十分でした。仕上げ工程では、砥粒が銅原子の化学結合を容易に切断して自由に動くことができるように、切削抵抗を十分に高くする必要があります。さらに、切削深さの増分は、原子の相互作用と直接的な関係があります。原子が堆積し始めると、研磨粒子がワークピースに入るまで切削抵抗が一貫して増加します。これには、定常状態の切削抵抗が必要でした。この比較的安定した段階で、切削抵抗の変動は、格子変形、格子再構成、アモルファス相変化、および切りくずの生成の程度にさらされました。砥粒が切削方向に沿って進むと、FCC格子の銅原子に外力が加わり、銅原子が変位しました。この変位はFCC格子を崩壊させ、転位を有する新しい格子構造に変換します。切削抵抗でも同様の状況が見られます。 [010]の方向に沿った切削力と粒子の衝突角度の間に正の線形相関はありません。 0°、5°、10°以降との衝突では、[010]方向の力は他の切削方向の力よりも小さく、変動も少なかった。バリは3.5〜15Åの高さ範囲で定義できるため、より小さな角度で切断し、基本的にバリを取り除きます。これらの方向を比較すると、切削深さが比較的小さければ、結晶構造の損傷や変形は中程度になります。したがって、切断プロセス全体で、図6bの曲線グラフに示すように、[010]方向に沿ったせん断力は小さく保たれました。シミュレーションの後の段階で、切削抵抗は最小0°に達しました。また、図6cに示すように、切削力は角度と直接的な関係があることがわかります。これは、粒子速度が80 m / sに達すると、より大きな切削角度が得られるためと考えられます。一方、同じシミュレーションステップでは、[001]方向に沿ったコンポーネントの速度が大きいほど、角度が大きくなり、粒子が深く切断され、より多くの原子格子が破壊されました。ただし、切削角度と切削抵抗には正の相関がありました。結晶粒が[100]方向に移動すると、C、Si、Cu原子間の摩擦が切削抵抗の原因となりました。そのため、切削抵抗は緩やかな増加傾向を示しませんでした。しかし、さらなるシミュレーションでは、切削力が増加して変動しました。これは、格子の変形と再構築、およびアモルファス構造相転移の生成と密接に関連していました。研磨粒子が破壊される前に、ワークピースの原子間の相互作用が達成されて材料が除去され、最終的には一貫して切削抵抗が増加します。臨界値（原子結合力）を超えて研磨切削力を増加させると、原子格子が損傷し、結合が解離してアモルファス構造になります。これを達成すると、切削抵抗は比較的低い値に低下しました。切削深さの増加により、アブレシブフロー加工の全過程で切削抵抗の変動が継続的に現れ、結晶構造の破壊がさらに進んだ。したがって、この段階では、切削抵抗の変動の最大値が大きかったと結論付けられます。図6bに示すように、シミュレーションの後の段階では、赤い領域がより大きな領域を占めていました。これは、切削抵抗が著しく上昇したことを示しています。同じシミュレーション時間で、切削角度が15°未満の場合、切削力は小さくなりました。これは、結晶格子のごく一部が破壊されたことを意味します。

SiCアブレシブインパクトカッティングプロセスのエネルギー分析

熱力学の総エネルギーは、システム内の全位置エネルギーと総運動エネルギーの合計であり、砥粒によってワークピースに対して行われた作業の影響を明らかにします。システムのエネルギー変化に及ぼす炭化ケイ素砥粒の切削角度の影響を図7に示します。炭化ケイ素砥粒を使用した単結晶銅被削材の切削工程では、被削材に砥粒が行う作業が作用します。 2つの方法で;一方は運動エネルギーに変換され、単結晶銅原子が炭化ケイ素粒子と接触して研磨する熱を増加させ、もう一方は位置エネルギーに変換され、単結晶銅ワークピースの内部構造、格子変形、および格子エネルギー放出。

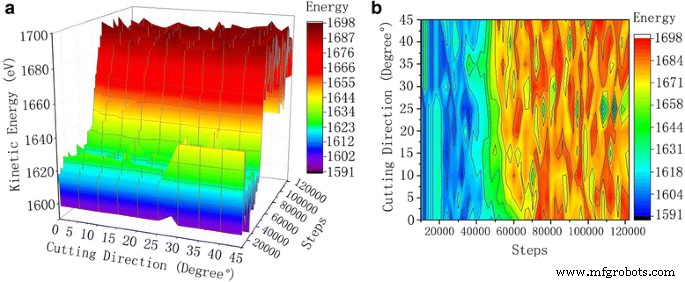
ワークピース原子の運動エネルギー曲線。図7は、切断プロセス中のさまざまな切断角度の運動エネルギー曲線です。シミュレーションステップ数の増加に伴い、原子の運動エネルギーは低い範囲で変動し、その後、変動内でより高い範囲に変動します。 a 3D曲線。 b 輪郭

単結晶銅ワークピースの砥粒切削プロセスでは、システムの運動エネルギーは、SiC砥粒によるワークピース材料の作業と密接に関連しています。システム内の粒子のあらゆる瞬間の速度を計算することにより、システムの総運動エネルギーを計算できます。

式では、\（{v} _ {\ mathrm {ix}} ^ 2 \）、\（{v} _ {\ mathrm {iy}} ^ 2 \）、および\（{v} _ {\ mathrm {iz}} ^ 2 \）は速度成分 x を表します 、 y 、 z それぞれ方向原子。

図7の運動曲線から、シミュレーションステップが増加すると、最初は原子の運動エネルギーが低い範囲で変動し、次に高い範囲で変動すると結論付けられました。砥粒の移動に伴い、最も外側の銅原子とSi、C原子（SiC）の間に長距離の反発相互作用が見られます。ワークピース内の銅原子は、運動エネルギーを取得して移動し始めます。炭化ケイ素粒子が銅の単結晶に接触すると、接触領域の原子温度が上昇し、原子の熱運動が上昇します。切削が安定すると、材料中の銅原子の運動エネルギーが動的平衡パターンで伝達および変換され、原子の運動エネルギーが高範囲で変動します。

運動エネルギーの分析により、切断プロセス中に粒子がワークピースに接触し始めると、押し出された領域の原子が格子変形し、原子座標が変化し、変位が運動エネルギーによって変化すると結論付けられました。研磨粒子が単結晶銅に入ると、ワークが完全にワークに入るときに単結晶銅ワークの運動エネルギーのピーク値が現れます。なぜなら、研磨粒子の運動エネルギーと位置エネルギーは単に相互に変換されるだけだからです。ただし、ワークピースに入る移動粒子を除いて、システム全体のエネルギーは変化しません。さらに、炭化ケイ素粒子の動きにより、ワークピースの原子が同時に移動します。原子摩擦中に発生する熱は、運動エネルギーによって放出され、転位運動によってひずみエネルギーが放出されます。

熱と運動エネルギーの変換は、次の式で計算されます。

式では、 n は原子の数です。 viは瞬間速度を表します。 k _B はボルツマン定数であり、 T _i は原子の温度です。

切削抵抗は、研磨剤が被削材に接触する領域の原子温度を上昇させます。原子の熱運動と原子の運動エネルギーを考慮すると、銅原子の運動エネルギーは部分的に増加します。シミュレートされたシステムは、正準集団に設定されています。システム全体の温度は一定の範囲で変動します。研磨粒子の切断中に発生する熱は、恒温原子層に急速に伝達されるため、システムの全体的な運動エネルギーはほとんど変化しません。

図8のポテンシャルエネルギー曲線からわかるように、シミュレーションステップ数を増やすと、ワークピース内の銅原子の単結晶間のポテンシャルエネルギーも増加する傾向があります。炭化ケイ素研磨剤が最初から完全に安定した切断まで銅ワークピースの単結晶に接触すると、ワークピースの材料が徐々に変形し、銅原子が変位し、結晶内の結晶格子の歪みにつながります。これにより、ひずみエネルギーが増加する弾性応力場も発生します。ひずみエネルギーが材料原子を再配列するのに十分でない場合、原子の転位が発生し、システムの総エネルギーが増加します。 0°から45°までのポテンシャル曲線とは対照的に、一定温度での原子の熱運動に一貫性があることがわかります。原子の運動エネルギーとSiC砥粒の切削角度の間に有意な関係はありません。原子の運動エネルギーは、原子の熱運動と密接に関係しています。ただし、位置エネルギーと総エネルギーの変化は、明らかにSiC砥粒の切削角度に関係しています。原子ポテンシャルエネルギーの大きさは、切断角度の増加とともに増加します。切断角度が0°から20°の間の場合、位置エネルギーの明らかな変化が観察されます。ただし、切断角度が25°〜45°の場合、位置エネルギーはそのまま残り、全体的な位置エネルギー曲線は0°〜20°の切断角度になります。図9に示すように、総エネルギーの傾向は位置エネルギー曲線の傾向と類似しています。すべての切断角度の合計エネルギー値は、互いに非常に近い値です。これは、総エネルギーがシステムの位置エネルギーと運動エネルギーに等しいのに対し、運動エネルギーは切断プロセス中に切断角度に合わせて変化しないためです。ワークピースの運動エネルギーの変化は、切削角度が異なると非常に小さくなります。したがって、位置エネルギーの変化曲線は、総エネルギーの曲線に似ています。図9の原子変位図を比較すると、同じ切削条件で、切削角度が25°〜45°の場合、単結晶銅ワークの切削深さが深くなることがわかります。これは、変位の増加に起因する可能性があります。銅原子の。 SiC粒子の[001]方向に沿って、格子および転位でより多くの原子損傷が生成されます。この間に生成されるひずみエネルギーはより高く、その結果、ワークピース原子のポテンシャルエネルギー変化曲線と総エネルギー変化曲線が高くなります。

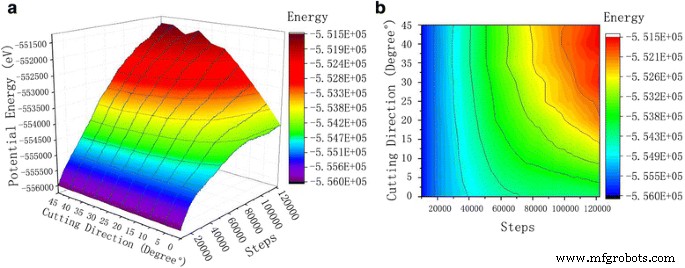
ワークピースの位置エネルギー曲線。図8は、切断プロセス中のさまざまな切断角度での位置エネルギー変動のグラフです。シミュレーションのステップ数が増えると、単結晶銅原子間のポテンシャルがワークピースを示すようになります。 a 3D曲線。 b 輪郭

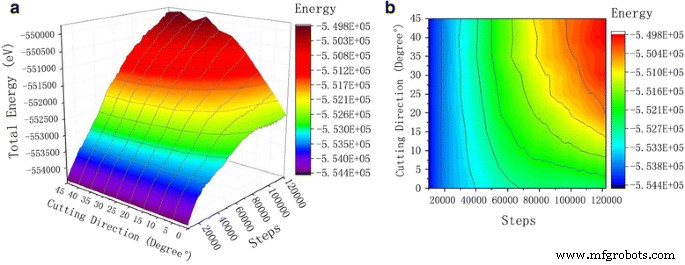
総エネルギー曲線。図9に総エネルギー曲線を示します。単結晶銅ワークピースをSiC切断する過程で、ワークピースへの砥粒の影響は2つの形で現れます。その一部は運動エネルギーに変換され、原子熱が増加し、研磨時に局所的な運動エネルギーが大きくなります。単結晶銅ワークピースとSIC粒子の接合面積。他の部分は位置エネルギーに変換され、単結晶銅ワークピースの内部構造が変化し、格子が変形し、格子エネルギーが放出されて位置エネルギーに変化します。 a 3D曲線。 b 輪郭

SiC研磨粒子の衝突切削プロセスにおける原子変位の分析

さまざまな角度での被削材の切削工程では、砥粒が切削方向に沿って移動し、被削材の銅原子を強制的に移動させます。ワークの移動方向の解析から、ワークの材質に対する砥粒の影響、切りくずの形成、材質の除去が完全に明らかになります。 Ackland-Jonesによって提案された結合角分析法によれば、観察目的と分析のために、異なる原子格子構造が多様な色でマークされています。個々のSiC粒子の切断過程を観察するためにZOY平面を選択し、図10からわかるように、切断領域の原子変位図を拡大します。

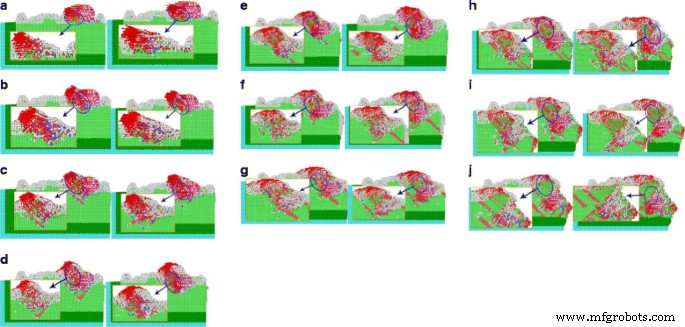
切断角度が異なると、原子の変位が発生します。図10は、さまざまな切断角度の原子変位を示しています。単結晶SiC砥粒が銅を異なる方向に切削するワークに衝突し、SiC砥粒を切削すると、切削方向の速度が80m / s、[001]方向の移動速度であるため、切削深さが増します。 v です _z =0.8 ∗ sin θ 、切削角度の切削深さを大きくすると、[001]同じ切削角度でシミュレーションステップが大きくなり、同時に切削深さが大きくなります。 a 0°変位。 b 5°の変位。 c 10°の変位。 d 15°の変位。 e 20°の変位。 f 25°の変位。 g 30°の変位。 h 35°の変位。 i 40°の変位。 j 45°の変位。 （原子色： HCP構造、 BCC構造、 白色のアモルファス構造としてのFCC構成）

単結晶SiC砥粒がワークピースと衝突して銅を異なる方向に切削すると、切削深さがプロセスに沿って増加します。切削方向の速度は80m / sで、[001]方向の部品速度は v です。 _z =0.8 ^∗ sin θ 。同じシミュレーションステップで、切削角度が大きくなると切削深さが増します。図10に示すように、ワーク材料の表面と内部の両方に原子位置シフトがあり、研磨粒子と接触します。ここで、異なる格子タイプの原子が互いに配置され、ドープされます。これらの砥粒の移動により、砥粒の先端に銅原子が蓄積し、砥粒の切削時にクラックが発生しません。研磨粒子の材料除去モードは塑性変形であることがわかります。同時に、研磨切削により、単結晶銅の原子変位は15°から45°に増加します。

砥粒運動方向に沿ったワーク原子数も増加し、原子変位は砥粒切削方向に垂直になります。原子変位のこの部分は、研磨粒子の変位によるものであり、切削動作をワークピース原子への押し出しに変更します。切削角度では、研磨粒子は0°から10°の間ですが、切削深さは15°から45°のものよりも浅いです。砥粒は主に切削機能を果たしており、ワーク原子の押し出しはわずかであり、変位方向が砥粒運動方向に垂直な原子数は少ない。多数の研磨粒子によるワーク表面の繰り返し切削により、切削角度の大きい研磨粒子は、切削プロセス全体でワーク材料に深いピットを生成しますが、切削角度が小さい研磨粒子は、前者によって生成された切削マークに沿って切削を続けます。 。複合作用の下で、ワークピース材料は特定の深さまで切断され（マイクロカッティング）、続いて全体のアブレシブフロー研磨が行われます。

SiCアブレシブ切削の転位衝突解析

転位は、特定の結晶表面と結晶方向に沿った結晶内の原子の特別な配置、または滑り面の滑りゾーンと滑り止めゾーンの間の境界です。転位は、刃状転位、らせん転位、混合転位に分けられ、混合転位が最も一般的です。研磨粒子の切断の過程で、単結晶銅のワークピースが塑性変形し、原子が移動し、結晶格子が破壊されて再構築され、その結果、多数の転位が発生します。異なる入射角での転位と結合角の分析を図10に示します。アブレシブフローシミュレーションのシミュレーションモデルでは、2つのアブレシブ粒子を使用してワークピースの材料を切断します。分析を容易にするために、図に示すように、切断プロセス中の単結晶銅材料のさまざまな転位線の生成と変化、および切断部分のさまざまな格子構造を、YOZ表面上の単一のSiC粒子のビューで分析します。 。11。

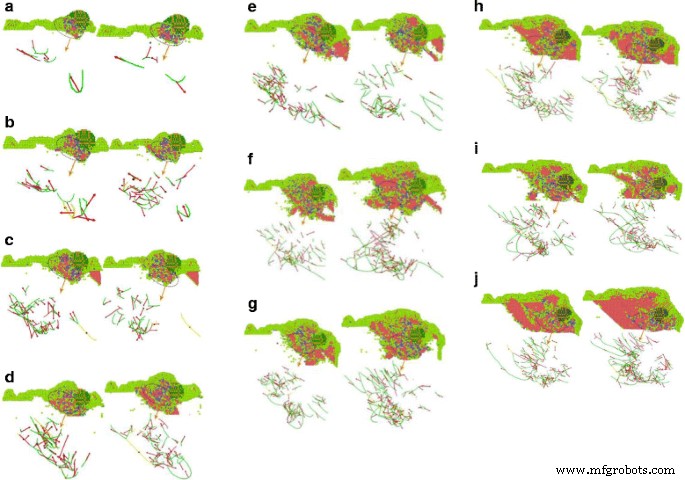
さまざまな角度-結合角転位折れ線グラフ。図11は、切断転位線と結合角を表しています。ワーク表面の繰り返し切削は研磨工程で多数の砥粒により行われるため、切削工程全体で切削角度の大きい砥粒はピットが大きくなり、切削角の小さい次の砥粒は研磨を続けます。カッティングトレース。そのため、被削材に一定の深さを持たせ、アブレシブフロー研磨のマイクロカッティング全体を実現しています。 a 切断角度が0°の転位線。 b 切断角度が5°の転位線。 c 切断角度が10°の転位線。 d 15°の切断角度の転位線。 e 20°の切断角度の転位線。 f 25°の切断角度の転位線。 g 30°の切断角度の転位線。 h 35°の切断角度の転位線。 i 切断角度が40°の転位線。 j 45°の切断角度の転位線。 （注：キー角度分析の上部、原子色の図： HCP BCC アモルファス構造 砥粒;転位線図の下部、図の転位線の色： 階段ロッド、 Shockley、 誕生、 Perect、 フランク、 バーガースベクトル）

各切断角度のキー角度分析図を図11に示します。ここでは、時間60および70 psでの内部ワークピースシミュレーションからのサンプルで、BADテクノロジーによる原子のさまざまな配置に従って原子が個別に着色されています。切削部の格子変化の解析を容易にするために、被削材のFCC構造の原子を除去します。 DXA技術により、さまざまな種類の転位がさまざまな色でマークされます。赤い矢印はバーガースベクトル（バーガースベクトル）、緑はショックリー部分転位（ショックリー）、水色はフランク部分転位（フランク）、ピンクの極位置は圧力誤差（ステアロッド）、転位全体が青色（パーフェクト）。

図11の結合角部分の分析からわかるように、外部の切削抵抗の影響下で多数の転位と格子変形が発生しました。結合角分析は、ワークピースの内部HCP構造が、切削角度の増加とともにより明確に現れることを示しています。さらなるシミュレーションでは、HCPの構造は徐々に増加します。炭化ケイ素粒子は、80 m / sの速度でワークピースの材料を連続的に切断および圧搾し、FCC構造からHCP構造への相転移をもたらします。この相転移の間、ワークピースの原子ひずみは増加し続けます。ただし、ワークピースの原子の応力状態が熱力学的相転移のしきい値を超えると、準安定状態になります。ひずみが増加すると、HCP相が核形成して自発的に成長し始め、銅のFCC格子が完全に不安定化して、機械的量が急激に変化します。原子の運動エネルギーは原子の温度に直接関係しているため（式1）、図7からわかるように、運動エネルギーの変化曲線には塩分が増加しています。これは、 HCPの核形成前の単結晶銅ワークピース。 HCP構造は、準安定核形成と部分的な応力解放によってシステム温度を上昇させます。研磨切削と押し出しにより、ワークピース材料の銅原子の結合が破壊され、無秩序になります。元の規則的な格子構造は壊れており、部分的な銅原子が徐々に無秩序に変化し、アモルファス構造を形成します。結合角分析図から、変位が比較的乱れた原子（図11）は、炭化ケイ素研磨粒子が原因で、60および70psでアモルファス構造を形成する傾向があることがわかります。同時に、同じ変位方向を持つ多くの原子がHCP構造に変換されます。一方、粒子は下向きにせん断され、元のアモルファス構造の原子の変位により原子構造が再配列され、HCPのアモルファス構造になります。次の切断段階の前でさえ、すでにHCP構造に変換された原子は、アモルファス構造に戻ります。切削深さが増すと、砥粒付近のアモルファス原子の数も増えます。

FCC結晶構造が研磨粒子によって切断されると、原子にせん断応力が発生し、その結果、格子内の原子が変位し、さまざまな格子構造が配置されます。ワークピースの原子を動かす際に、原子の剛直な変位は転位を生成します。これは転位線とも呼ばれます（図11）。転位線は、すべり面のすべり帯と非すべり帯の境界と言えます。転位とPATSベクトルの関係によれば、転位はPATSベクトルと平行であり、らせん転位と呼ばれます。垂直転位は刃状転位であり、混合転位は平行でも垂直でもありません。図11では、ほとんどの転位線は、典型的な混合転位であるPATSベクトルに対して平行でも垂直でもありません。研磨粒子の切断プロセスでは、転位線が変化し、移動し、研磨粒子の周りで成長します。粒子が近いほど、転位線の密度が高くなります。原子の配置が複雑な場合、転位線も非常に密になります。オレンジ色でマークされた研磨粒子は、それらの周りに大量のHCP、BCC、およびアモルファス構造を生成します。これらは互いに絡み合って混ざり合い、結晶の内部エネルギーを増加させる転位を形成します。原子が図12bに示すように自己を配置するとき、最大の位置エネルギーを持ちます。図12a–bに示すように、配置の場合、原子は最も低い位置エネルギー位置に配置されます。転位線の数は、結晶のひずみエネルギーの大きさに直接関係しています。単位長転位の総ひずみエネルギーは、次の式で測定できます。

転位変化の概略図。転位は、結晶中の原子の特別な配置です。これは、ある結晶面に沿って原子配列にある結晶であり、ある間違った線で結晶方位が発生し、すべりが発生した領域とすべりが発生していない領域のすべり面の境界です。図12 a – c 、上部原子と下層原子の剛性の相対変位は転位を生成し、上部原子は滑り領域に属し、下部原子は滑り止め領域に属し、それらは交差線の滑り面にあります。転位線、つまり転位と呼ばれます。図12は、転位の生成と発達のプロセスです

ここで、α に関連する幾何学的因子（タイプ転位、転位密度）パラメータであり、通常は0.5〜1.0です。 G はせん断弾性率、 b は滑り距離です。

ワークピース材料が切断されると、粒子が原子配列を破壊し、格子が再構築されます。これは、巨視的には、ワークピース材料の塑性変形を構成します。塑性変形の過程で、転位は結晶から脱出し、転位密度を減少させると考えられていました。ただし、この転位密度は転位の伝播により増加します。転位増倍には多くの方法があり、主なものはフランク-リード転位源理論であり、その成長メカニズムを図11に示します。図11に示すように、転位線の密度は60から切削シミュレーションが進行したら70ps、フランク-リード転位源理論に従って転位線の数と形状の両方を変更します。 60 psのシミュレーション時間では、多くの長いShockley転位があります。しかし、さらに10 psのシミュレーションの後、長いShockley転位線はますます短くなります。元の直線転位線は曲がった状態に変わります。これは特に砥粒の近くで顕著です。式3から、転位のひずみエネルギーは b に比例します。 ² 。エネルギーの観点から、 b が最小の転位 結晶中は低エネルギーで最も安定しているはずです。ただし、 b が大きい転位 1つに分解されます。また、転位のエネルギーは転位線の単位長さで評価されます。 2点間の最短線が直線であるとすると、直線転位のひずみエネルギーは曲がったものよりも低く、直線転位の方が安定していることを意味します。フランク-リード転位源理論は、長い転位線が短くなり、より小さな転位に分解されるため、結晶のひずみエネルギーが減少すると主張しました。

ワークピース表面と研磨粒子間の摩擦係数の分析

SiC砥粒切削単結晶銅材料の機械的性質と表面効果を定量的に明らかにするために、切削面の接線力（[010]方向）と法線力（[001]方向）をさらに分析します。摩擦係数は、法線力に対する接線力の比率として定義できます。式は次のとおりです。

図13は、研磨切削中のさまざまな切削角度に沿った摩擦係数の変化を示しています。摩擦係数の変化は2つの期間に分けることができます。期間I、切削距離が研磨粒子のサイズの半分未満の場合、材料の表面効果により、摩擦係数が特定の範囲で激しく変動します。一方、期間IIでは、すべての摩擦係数は非常に小さな範囲で変動し、摩擦係数はさまざまな角度で定常状態を維持します。ただし、切削角度5°では、シミュレーション終了時に若干の異常変動があります。さらに、期間Ｉでは、研磨粒子がワークピースの原子に接触し、研磨粒子が研磨直径の半分のワークピースに入り（図１３ｂに示される）、切削移動距離は７．５Åに達する。図6では、切削抵抗の変化曲線は、接線力と垂直力が期間Iで振動相にあることを示しています。摩擦係数は、接触面の原子間の接着として特徴付けることができ、2つの原子に関連しているためです。図13aに示すように、切削モードに関係なく、切削角度の変化が摩擦係数の大きな変化を引き起こさないという現象を解釈できる、互いに接触します。

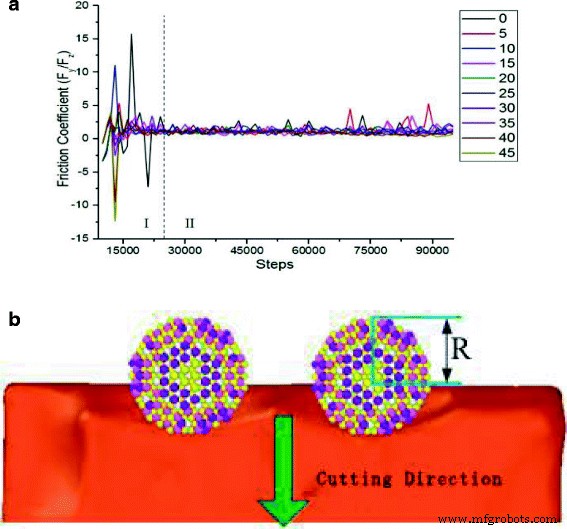
さまざまな切断角度の摩擦係数。図13は、SIC粒子が単結晶銅をさまざまな角度から切断する際の摩擦係数の変化です。切削角度の変化は摩擦係数の大きな変化を引き起こしませんでした。切断モードに関係なく、切断プロセスで関連する原子と接触する2種類の摩擦係数について説明しました。 a 切削角度による摩擦係数変動曲線。 b SiC砥粒が7.5Å移動する瞬間構造

結論

SiC研磨粒子による単結晶銅のマイクロカッティングシミュレーションは、研磨フロー研磨中に実現されます。 SiC研磨剤の切削を包括的に分析すると、SiC研磨剤粒子が0°から15°の角度で切削すると、 Y に沿って切削力が発生することがわかります。 および Z 方向は比較的小さく、安定している傾向があります。切削角度が大きいほど転位が多くなり、溝が大きくなり、被削材に損傷を与えます。切断の過程で、結晶材料のすべての側面の性能に即座に悪影響を与えるより多くの転位を避ける必要があります。したがって、0°の切断角度は他の角度よりも優れています。発生する転位の量、または切削プロセスでの切削力とエネルギーの変化を考慮します。小または中角度での切断は、表面品質を向上させるだけでなく、内部欠陥を減らすのにも役立ちます。