2種類の2D炭素同素体の熱伝導率：分子動力学研究

はじめに

ダイヤモンド[1]、カーボンナノチューブ[2,3,4,5]、グラフェン[6,7,8,9,10,11,12]などの炭素材料は、その優れた性能により、多大な研究関心を刺激してきました。熱輸送特性。特に低次元炭素材料は、熱輸送において優れた特性を示します。 1D材料として、単一のカーボンナノチューブの高い熱伝導率（TC）が、実験[2、3]および理論的研究[4、5]によって観察されています。さらに、グラフェンは、単一原子の厚さの平らな2次元（2D）炭素材料として、その高いTCにより、次世代の熱伝導性強化複合材料の革新的な材料と見なされています[6,7,8,9,10 、11、12]。グラフェンのTCはグラフェンの40％に達する可能性があり、熱管理に応用できる可能性があることも報告されています[13、14、15]。

これらの炭素同素体の魅力的な特性に触発されて、研究者は近年、炭素同素体とその誘導体を研究するために集中的な努力をしてきました。 sp ² などの新しい2D炭素同素体を調査するために、実験的および理論的アプローチが採用されています。 -5員、6員、および7員の環を持つ炭素層のようなもの[16]。 4員環を持つ2Dアモルファスカーボン[17];平面カーボンペンタヘプタイト[18];パターン化された欠陥を持つ2Dカーボン半導体[19];いくつかの2Dフラットカーボンネットワーク[20];オクタグラフェン[21]; T-グラフェン[22];およびH-net [23]。これらの2D炭素同素体の固有の特性の特定は、電子、フォトニック、および熱場における次世代のナノ材料にとって重要です[16、17、18、19、20、21、22、23]。

2D炭素同素体の新しい構造を探求することへの関心が高まるにつれ、Su etal。 [24]は、第一原理計算により、八角形と五角形で構成される2つの新しいエネルギー的に競争力があり速度論的に安定な2D炭素同素体を提案しました。これら2つのカーボンシートの速度論的安定性は、それらのフォノン分散曲線を計算することによって確認されました。これらの2つの炭素同素体の構造は、直線経路とジグザグ経路に沿って5-5-8員環（558）リボンをコピーしていると見なすことができるため、これら2つの炭素同素体はオクタゴンと呼ばれます。五角形グラフェン線（OPG-L）と八角形および五角形グラフェン-ジグザグ（OPG-Z）。これら2つの炭素同素体の形成エネルギーは、それぞれ0.31 eV /原子と0.34eV /原子です。この値は、以前に合成されたグラフィンの形成エネルギーよりもはるかに低く、0.76 eV /原子です[25]。 OPG-Zは、電子デバイスに応用できる可能性のある電子構造の顕著な異方性を持っていることに注意してください[24]。したがって、OPG-LおよびOPG-Zの電子アプリケーションの要件を満たすには、2つの新しい構造の熱放散特性を研究することが避けられず必要です。今まで、これら2つの構造の熱特性はまだ明確ではありません。

この作業では、分子動力学シミュレーションを使用して、2つの新しい2D炭素同素体の熱特性を調査します。 TCに対するサイズ、ひずみ、および温度の影響が調査されます。結果は、フォノンの振動状態密度（VDOS）を計算することによって分析されます。これら2つの炭素同素体の熱特性に関する調査では、熱管理デバイスへの応用の可能性が示されています。

モデルとメソッド

OPG-L（図1a）とOPG-Z（図1b）の構造には、八角形と五角形で構成される代表的なセルが含まれています[24]。構造のエッジタイプを区別するために、グラフェンと同じようにアームチェアとジグザグのキラリティーを定義します（図1を参照）。これらの2つの構造は、緑の列に沿った並進対称性を使用して、赤の原子で示される代表的な558リボンによって形成できます。

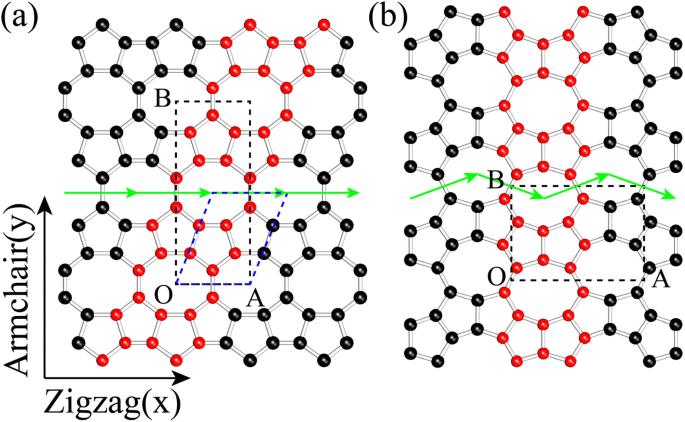
a の概略モデル OPG-Lおよび b OPG-Z。黒の破線のフレームは、OPG-LとOPG-Zの直交単位セルです。ここで、OAとOBは格子ベクトルです。 OPG-Lのプリミティブセルは青い破線の枠で示されていますが、OPG-Zのプリミティブセルはクリスタルセルと同じです

すべてのMDシミュレーションは、大規模な原子/分子の大規模並列シミュレーター（LAMMPS）パッケージを使用して実行されます[26]。 LindsayとBroidoによる最適化されたTersoffポテンシャル[27]を使用し、わずかな変更、つまり、変更された最適化されたTersoffポテンシャルを使用して、炭素原子間の相互作用を記述します。 LindsayとBrodioは、元のTersoffポテンシャル[28]と比較して2つのパラメーターを最適化しました。1つは平衡結合角用で、もう1つは引力相互作用強度用です。この最適化されたTersoffポテンシャル[27]によると、グラフェンの平衡結合長は1.4388Åであり、実験値の1.42Å[29]よりも長くなっています。 Tersoffポテンシャルの長さに関連するパラメータはλのみであるため ₁ 斥力関数（ f ^R = A exp。（-λ ₁ r ））およびλ ₂ 魅力的な機能で（ f ^A = B exp（-λ ₂ r ））、これら2つのパラメータに1.4388 / 1.42の係数を掛けることにより、正しい結合長を得ることができます。つまり、λを変更します ₁ 3.4879Å ^-1 から 3.5333Å ^-1 λを変更します ₂ 2.2119Å ^-1 から 〜2.2407Å ^{− 1} 。これらの変更は、グローバルな方法でポテンシャルの長さスケールを変更するだけです。この修正された最適化されたTersoffポテンシャルに基づくと、MDシミュレーションの対応する平衡格子定数は次のとおりです。OPG-LではOA =3.63Å、OB =9.38Å、OPG-ZではOA =6.78Å、OB =5.04Åです。 Suらの以前の研究とよく一致している。 [24]、つまり、OPG-LではOA =3.68Å、OB =9.12Å、OPG-ZではOA =6.90Å、OB =4.87Å。

逆非平衡分子動力学（rNEMD）[30]シミュレーションは、TCを計算するために実行されます。周期境界条件は、x次元とy次元で採用されています。 OPG-LおよびOPG-Zの構造は、最初は共役勾配アルゴリズムのPolak-Ribieredバージョン[31]を介して最適化され、後でシステムが確実に到達するように0.25nsのNosé-Hoover熱浴[32、33]が採用されます。 300 Kでの平衡状態（0.25 fsのタイムステップ）。平衡状態に近づいた後、モデルは熱伝達方向に沿って50個のスラブに分割されます。図2aに示すように、1番目のスラブがヒートシンクとして割り当てられ、26番目（サンプルの中央のスラブ）が熱源であり、熱流束が熱源（高温領域）からヒートシンク（寒冷地）。熱流束の輸送方向は長さ方向（L）として定義され、横方向は幅（W）方向として定義されます。熱流束Jは、熱シンクスラブ内の最も高い運動エネルギーを持つ最も高温の原子と熱源内の最も低い運動エネルギーを持つ最も低温の原子の間で運動エネルギーを交換することによって、これら2つのスラブ間で放出/注入されます。スラブ。熱流束Jは、次の式に従ってヒートシンクと熱源スラブの間の運動エネルギーの交換量を計算することによって取得できます。

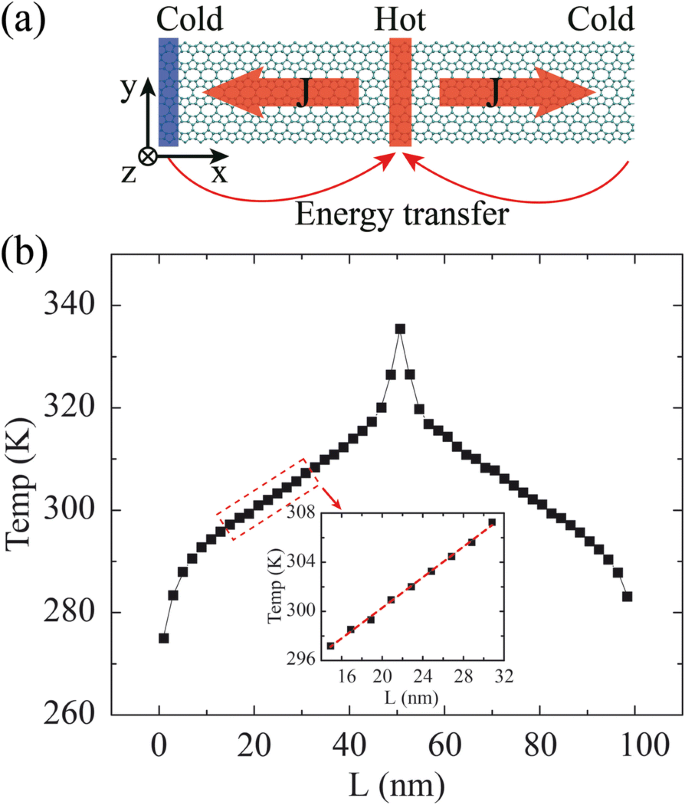
a rNEMDメソッドの概略プロット。熱流束は、熱源（高温領域）からヒートシンク（低温領域）に移動します。熱流束の輸送方向は長さ方向（L）として定義され、横方向は幅（W）方向として定義されます。 b スラブの関数としての平均気温の分布

ここで t _スワップ は運動エネルギーを交換する合計時間 N _スワップ 交換する原子ペアの量を示します m は原子の質量であり、 v _h および v _c それぞれ、原子（ヒートシンクスラブで最も高い運動エネルギーを持つ最も高温の原子と、熱源スラブで最も低い運動エネルギーを持つ最も低温の原子）を交換する速度を表します。各スラブの温度が収集され、3.0 nsにわたって平均化されて、システムが非平衡定常状態に達したとき（1.5 ns後）の温度分布が取得されます。 TCの値（κ ）は、フーリエの法則を使用して計算されます

ここで A は熱伝達の断面積（ A モデルの幅と厚さを乗算して得られます）、および∂T / ∂L システムが非平衡定常状態に達した後の温度勾配を示します（図2bを参照）。係数2は、熱流束が熱源から離れる2つの方向に輸送されるという事実を表しています。モデルの厚さは、グラフェンの層間平衡間隔（0.34 nm）[8、10、34、35]であると想定されています。

結果と考察

最初に、2つの炭素同素体のTCに対するシステムサイズの影響を調べます。シミュレーションサンプルは、同じ幅3 nmで生成されますが、長さは50〜1000nmで異なります。この作業で言及されているサンプルの長さの値はすべて、有効長（ L ）であることに注意してください。 _eff ）熱伝達の。つまり、有効なサンプルの長さはサンプルの長さの半分（ L ）です。 ）、つまり L _eff = L /2。これは、rNEMDメソッドでサンプルの中央（熱源）から両端（ヒートシンク）に移動する熱流束に起因します。特に、長さが50 nmで、幅がそれぞれ3 nm、6 nm、9 nm、12 nmと異なるサンプルの熱伝導率を計算することにより、TCがサンプル幅に依存しないことを確認しました。図3.ジグザグに沿ったOPG-LのTCとアームチェアの方向は、κと名付けられています。 _OPG-LZ およびκ _OPG-LA 、 それぞれ。同様に、κ _OPG-ZZ およびκ _OPG-ZA ジグザグとアームチェアの方向に沿ったOPG-ZのTCを表すために使用されます。シミュレーション結果は、2つのキラル方向のOPG-LとOPG-ZのTCが、サンプルの長さが50〜1000nmの範囲で単調に増加することを示しています。これは、長いサンプルでは、​​より長い波長の音響フォノンが熱伝達に関与しているためです[9、36]。それぞれ、ジグザグ方向に沿った長さ50nmおよび1000nmのOPG-LおよびOPG-ZのTCはκです。 _OPG-LZ50 =125 W / mK、κ _OPG-LZ1000 =296 W / mK、κ _OPG-ZZ50 =94 W / mK、およびκ _OPG-ZZ1000 =236 W / mK。アームチェアの方向に沿って、OPG-LとOPG-ZのTCはκです。 _OPG-LA50 =105 W / mK、κ _OPG-LA1000 =316 W / mK、κ _OPG-ZA50 =93 W / mK、およびκ _OPG-ZA1000 =214 W / mK。

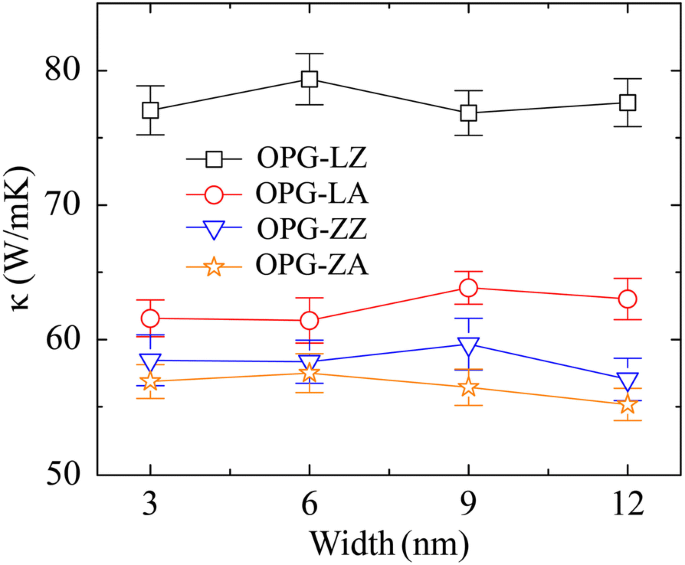
幅の関数としてのOPG-LおよびOPG-ZのTC

無限に長いサンプルのTCを抽出するために、逆フィッティング手順が採用されています。逆数と逆TCの関係は、[37,38,39]：

ここでκ _∞ 無限サンプルの外挿されたTC、 l はフォノンの平均自由行程であり、 L _eff は熱伝達の有効長さです。式（3）は、逆数と逆TCの関係が線形であることを示しています。図4に示すように、長さの逆数とTCの逆数の間に線形関係が見られます。 L ^-1 に外挿する =0、無限サンプルのTC、つまりκ _OPG-LZ =310 W / mK、κ _OPG-LA =332 W / mK、κ _OPG-ZZ =247 W / mK、およびκ _OPG-ZA =228 W / mK、取得されます。

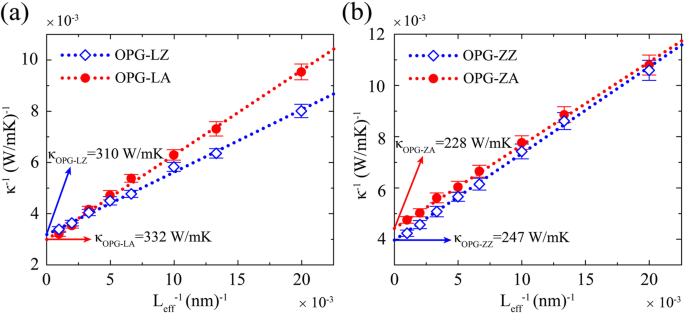
a の逆TC OPG-Lおよび b 300 Kでのサンプルの逆数の関数としてのOPG-Z。白抜きの青いひし形と赤い点は、それぞれジグザグ方向とアームチェア方向に沿ったTCを表します

さらに、20 nmの同じ長さと幅のサンプルを確立することにより、平衡分子動力学（EMD）法で実行中のTCを表現します（このシミュレーションサンプルサイズは、有限サイズの影響を排除するのに十分な大きさであることがテストされています） 。ファンらの仕事によると。 [39、40]、EMD法でのTC計算は、グリーン久保公式[41、42]に基づいており、x方向に沿った実行TCは次のように表すことができます。

ここでκ _B ボルツマン定数 V システムのボリューム、 T システムの絶対温度、< J _x （0） J _x （ t ^' ）〉は、熱流束の自己相関関数 t です。 は相関時間であり、 J _x x方向の熱流束です。記号〈〉は、EMDシミュレーションの時間平均を表します。最大相関時間は2nsであり、十分な長さであることがテストされています。図5に示すように、300 Kでの2つのキラル方向でのOPG-LとOPG-Zの実行TCは、異なる初速度での100回の独立したシミュレーションの結果を平均することによって表されます。 1.0〜2.0 nsの相関時間で実行中のTCを平均することにより、無限サンプルのTCをさらに取得できます。つまり、OPG-LZ、OPG-LA、OPG-ZZ、およびOPG-ZAの収束TCは、それぞれ313 W / mK、344 W / mK、261 W / mK、および233 W / mKです。 rNEMD法での外挿による結果との合理的な一致。

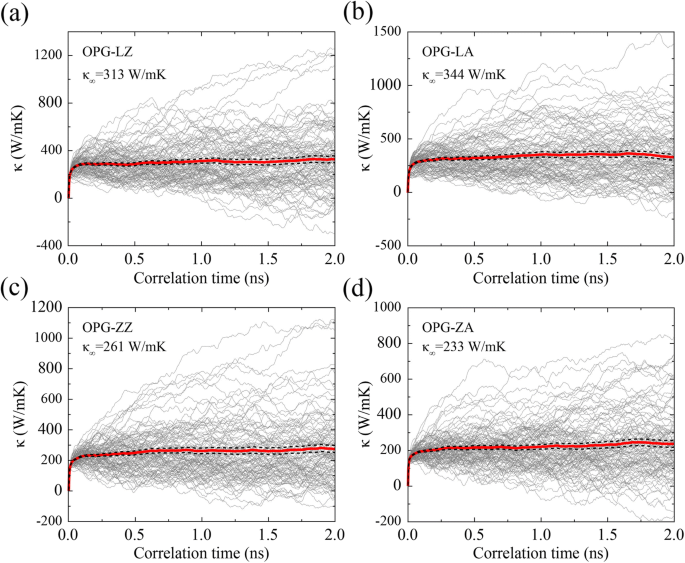
a のTCの進化 OPG-LZ、 b OPG-LA、 c OPG-ZZ、および d 相関時間の関数としての300KでのOPG-ZA。細い線は100の独立したシミュレーションの結果を表し、太い実線と破線はそれらの平均と誤差の範囲を表します。 κ _∞ は無限サンプルのTCであり、1.0〜2.0nsの相関時間で実行中のTCを平均することによって取得されます

これら2つの炭素同素体のTCは、グラフェンのTC（3000〜5000 W / mK）よりもはるかに低いことがわかります[7、43] 。 この現象を説明し、物理的な洞察を探求するために、3つの重要なパラメータ、つまり C を計算します。 _v 、 v _g 、および l 、古典的な格子熱輸送方程式に基づく：

ここで、C _v は熱容量、v _g は有効フォノン群速度、lはフォノン平均自由行程です。

長さと幅の両方が20nmのサンプルを採用して、300 Kでの熱容量を調査します。熱容量は、平衡分子動力学へのアプローチで使用されているMcGaughey and Kaviany [44]のアプローチに従って計算されます。シミュレーション[45]。総エネルギー E を計算します T の温度で =290 K、295 K、300 K、305 K、310 K、正準集団で、結果は、異なる初速度での10回の独立したシミュレーションの60psにわたって平均化されます。図6に示すように、エネルギー-温度曲線の線形フィッティングの傾きが熱容量です。

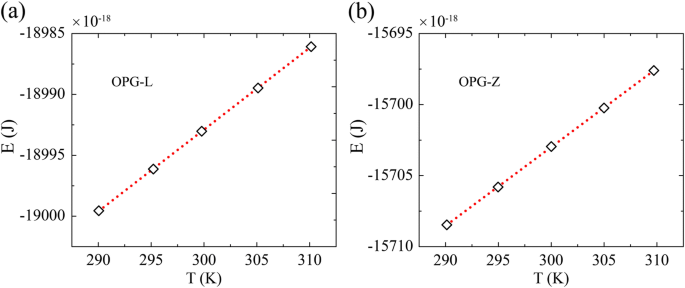
a の温度の関数としてのエネルギーの変化 OPG-Lおよび b OPG-Z。エネルギー-温度曲線の傾きは熱容量を示します。対応する熱容量は、原子あたりそれぞれ4.163 E-23 J / Kと4.126E-23 J / Kです

ここで計算するフォノン群速度は、実効フォノン群速度 v であることに注意してください。 _g 平均フォノン群速度ではなく v 。図7に示すように、実効フォノン群速度は、rNEMDとEMDシミュレーションの結果を比較することで取得できます。つまり、有効なシステム長 L _eff 相関時間の上限を乗算することにより、EMD法で定義できます t Green-Kuboの式で（4）実効フォノン群速度 v による _g 、 L _eff ≈ v _g t 。実行中のTC κ （ t ）EMD法の）は、システムの長さκの関数と見なすこともできます。 （ L _eff ）。平均フォノン群速度と比較すると、実効フォノン群速度は概算ですが、低次元格子モデル[46]での熱輸送の研究に広く使用されており、グラフェン[40]や同素体にも使用されています。 Si [39]。

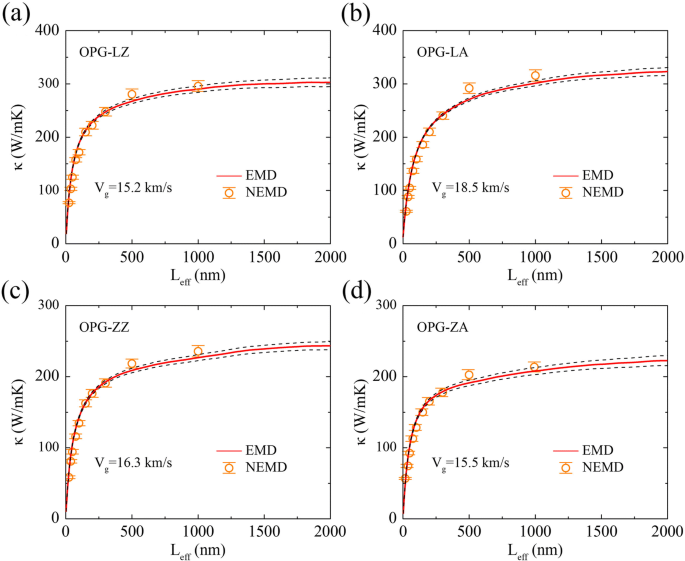
a のTC OPG-LZ、 b OPG-LA、 c OPG-ZZ、および（ d ）EMDおよびrNEMDシミュレーションからの有効サンプル長の関数としてのOPG-ZA。実効フォノン群速度 V _g EMDシミュレーションとrNEMDシミュレーションを組み合わせて得られます

式に基づく。 （3）、フォノンの平均自由行程は、rNEMD法の外挿によって得ることができます。これら2つの炭素同素体のTCをグラフェンのTCと比較するために、グラフェンのこれら3つのパラメーターも示します。グラフェンの熱容量は上記の方法で計算されますが、他の研究では有効フォノン群速度とフォノン平均自由行程が得られます[7、40]。これら2つの炭素同素体の熱容量はグラフェンの熱容量に近いことがわかります。ただし、有効フォノン群速度とフォノン平均自由行程はグラフェンよりもはるかに低いため、2つの材料のTCが低くなります（表1を参照）。

さらに、図8に示すように、TCの温度依存性を調べます。200Kから300 Kの温度領域が、私たちが焦点を当てている主要な範囲です。シミュレーションサンプルは、同じ幅3 nmで、長さがそれぞれ50 nm、75 nm、100 nm、150 nm、200nmで生成されます。図8a、bに示すように、さまざまな温度でのOPG-LZとOPG-LAの逆TCを、逆サンプル長の関数として示します。 300 Kでのサイズ効果の外挿と同様に、さまざまな温度での無限サンプルの熱伝導率は、外挿手順を実行することによって抽出されます。図8c、dに示すように、すべての収束熱伝導率は、300 K（κ）でのTCによって正規化されます。 ₀ 。

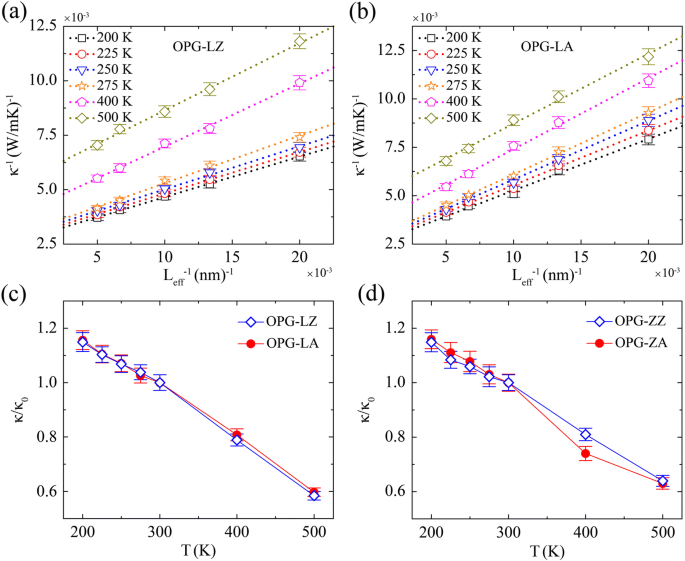
a の逆TC OPG-LZ、 b 逆サンプル長および相対TC（κ）の関数としてのさまざまな温度でのOPG-LA / κ ₀ ）の c OPG-Lおよび d 温度の関数としてのOPG-Z。 κ ₀ は300KでのTCであり、κの場合は310W / mK、332 W / mK、247 W / mK、および227 W / mKです。 _OPG-LZ 、κ _OPG-LA 、κ _OPG-ZZ 、およびκ _OPG-ZA 、それぞれ

図8は、ジグザグ方向とアームチェア方向の両方に沿って、OPG-LとOPG-Zの両方の温度が上昇するにつれてTCが低下することを示しています。 TCの傾向は温度によって変化し（200〜500 K）、グラフェンに関する以前のTC研究の傾向とよく一致しています[8、36、47]。この現象は、熱輸送において重要な役割を果たすウムクラップ散乱過程の強化に由来します[8、36、47]。さらに、温度が300〜500 Kの場合、κ _OPG-LZ 、κ _OPG-LA 、κ _OPG-ZZ 、およびκ _OPG-ZA それぞれ42％、40％、36％、37％低下します。これら2つの炭素同素体のTCの温度依存性は、実際のアプリケーションでは温度の影響を考慮する必要があることを示しています。

グラフェン[48、49]、シリセン[34、50、51]、フォスフォレン[37]などの2次元材料の熱特性は、ひずみ工学に敏感です。サイズの小さいグラフェンのTCは、引張ひずみの増加とともに減少することが報告されており[48]、サンプルが500μmより大きい場合はひずみを増加させることによってTCを向上させることもできます[49]。 TCのサンプルサイズとひずみへの異常な依存性は、境界散乱とフォノン-フォノン散乱の間の競合に起因します。さらに、シリセンのTCは、小さな引張ひずみでは増加しますが、面内モードでのフォノン軟化と面外モードでのフォノン硬化との競合により、大きなひずみでは減少することがわかります[34、50、 51]。したがって、OPG-L構造とOPG-Z構造の両方について、TCの動作と引張ひずみの関係を調査することが重要であり、必要です。

まず、これら2つの炭素同素体の機械的特性を調べます。サンプルサイズは、長さ約5 nm、幅5nmです。偽の高い結合力と非物理的なひずみ硬化を回避するために[52、53]、カットオフ距離は（ R に固定されています。 = S =1.95Å）。修正された最適化されたTersoffポテンシャルのこのカットオフ距離は、C-C結合のシミュレーションに使用されていた以前のTersoffポテンシャル（1.8〜2.1Å）[28、53、54、55]のカットオフ距離とも一致しています。すべてのシミュレーションは、構造の原子構成を最小のポテンシャルエネルギー状態に緩和することによって開始されます。一軸引張ひずみは、0.0002 ps ^-1 のひずみ速度で適用されます。 。グラフェンの層間平衡間隔（3.4Å）は、2つの構造の層間平衡距離を表すために使用されることに注意してください。これら2つの炭素同素体の機械的特性を、グラフェンとグラフェンの比較とともに表2に示します[56]。 z の上付き文字の特徴 および a それぞれジグザグシートとアームチェアシートを表します。

表2から、ジグザグ方向に沿ったOPG-LとOPG-Zのヤング率は538GPaと492GPaであり、アームチェア方向に沿ったヤング率はそれぞれ648GPaと550GPaであることがわかります。これは、OPG-LとOPG-Zのヤング率がグラフィンのヤング率（503.1 ^z ）に近いことを示しています。 および525.0 ^a ）がグラフェンよりも低い（856.4 ^z および964.0 ^a ）。ジグザグ方向とアームチェア方向に沿った2つの炭素同素体の応力-ひずみ関係を図9に示します。これら2つの炭素同素体の破壊挙動に従って、これら2つの炭素同素体の極限ひずみ（張力）をさらに取得します。それぞれ、ジグザグ方向に沿って、OPG-LとOPG-Zの極限ひずみ（張力）は17.2％と10.9％であり、アームチェア方向に沿って、極限ひずみ（張力）は8.7％と7.9％です。 OPG-Lの構造は、ジグザグ方向の引張ひずみ下で強度が高いことがわかりました。ただし、グラフェンやグラフェンと比較すると、2つの炭素同素体の極限ひずみ（張力）は低くなります。

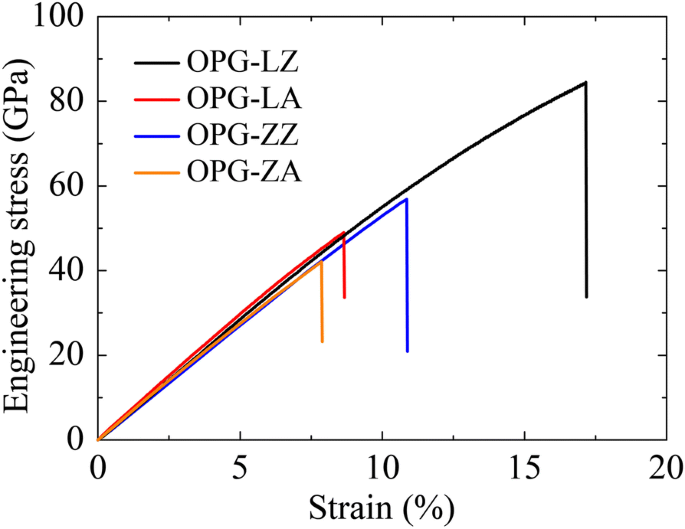
ジグザグ方向とアームチェア方向に沿った2つの炭素同素体の応力-ひずみ関係

次に、熱伝達方向に沿って一軸引張ひずみを適用することにより、これら2つの炭素同素体のTCに対するひずみ効果を調べます。シミュレーションサンプルの幅は同じですが、長さはそれぞれ50 nm、75 nm、100 nm、150 nm、200nmです。さまざまなひずみでの無限サンプルの熱伝導率は、外挿手順を実行することによって抽出されます（図10a、bを参照）。図10c、dに示すように、すべての収束熱伝導率は、300 Kでの無応力のTC（κ）によって正規化されます。 ₀ ）、さらに相対TC（κ / κ ₀ ）さまざまな一軸ひずみの関数としての2つの炭素同素体の。図10は、OPG-LとOPG-Zの両方のTCが引張ひずみの増加とともに単調に減少することを明確に示しています。これは、グラフェン[34、48]の以前の研究と一致していますが、シリセン[34、50、51]とは対照的です。フォスフォレン[37]。図10に示すように、κの最大削減量 _OPG-LZ 、κ _OPG-LA 、およびκ _OPG-ZZ 、κ _OPG-ZA それぞれ49％、44％、37％、31％です。特に、ジグザグ方向に沿ったOPG-LのTCは、広範囲のひずみによって調整できます。

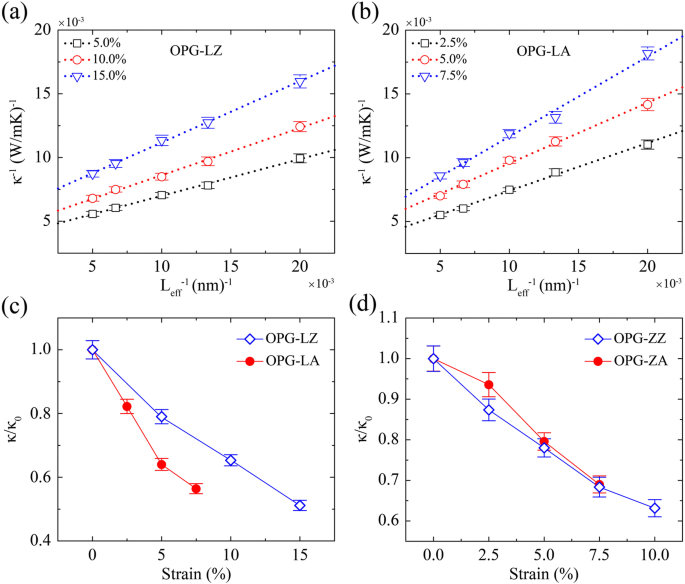
a の逆TC OPG-LZ、 b 逆サンプル長の関数としてのさまざまな一軸ひずみでのOPG-LA、および相対TC（κ / κ ₀ ）の c OPG-Lおよび d ひずみの関数としてのOPG-Z。 κ ₀ は300KでのストレスフリーのTCであり、κの場合は310W / mK、332 W / mK、247 W / mK、および227 W / mKです。 _OPG-LZ 、κ _OPG-LA 、κ _OPG-ZZ 、およびκ _OPG-ZA 、それぞれ

OPG-LおよびOPG-Zの熱輸送特性に対するひずみの影響をさらに解明するために、典型的なひずみでのOPG-LZのフォノンのVDOSを計算します。 VDOSは、原子速度の自己相関関数のフーリエ変換によって計算されます。関数は次のように定義されています：

図11に示すように、面内および面外方向のフォノン軟化（赤方偏移）が観察されます。この現象は、引張ひずみ下のグラフェンに関する以前の研究とよく一致しています[34、48]。特に、面外方向のVDOSと比較すると、面内方向のフォノン軟化は明らかです。これは、OPG-LとOPG-ZのTCの低下は、主に面内方向のひずみ誘起フォノン軟化によるものであることを示しています。

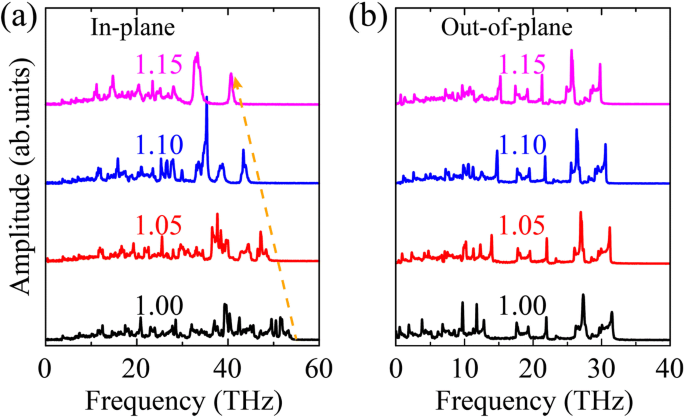
面内 a および面外 b OPG-LのVDOSとジグザグ方向に沿った一軸引張ひずみ

結論

要約すると、EMDシミュレーションとrNEMDシミュレーションの両方が実行され、八角形と五角形で構成される2つの新しい2D炭素同素体の熱特性が調査されました。サイズ、温度、およびTCに対するひずみの影響が得られます。私たちの結果は、TCがサイズの増加とともに単調に増加することを明らかにしています。無限のサイズの熱伝導率は、逆数と逆TCの線形関係によって得られます。逆非平衡分子動力学法の外挿によって得られた収束TCは、平衡分子動力学法のそれと合理的に一致していることがわかります。グラフェンと比較してはるかに低いTCは、フォノン群速度とフォノン平均自由行程が低いことに起因します。私たちの調査結果は、OPG-LおよびOPG-Zの熱輸送特性に対するサイズ、温度、およびひずみの影響に関する重要な洞察を提供し、マイクロ/ナノエレクトロニクス分野の熱管理デバイスにおける潜在的なアプリケーションを示しています。

略語

558：

五五八員の指輪

OPG-L：

八角形と五角形のグラフェンライン

OPG-Z：

八角形と五角形のグラフェン-ジグザグ

rNEMD：

非平衡分子動力学を逆にする

TC：

熱伝導率

VDOS：

状態の振動密度