分子動力学法を用いた金基板上のグラフェンのナノスケール摩擦挙動の研究

背景

グラフェンは、幅広い潜在的な用途の中で、ナノスケールの電子機器に応用できる有望な新材料の1つです[1,2,3,4,5]。実際のグラフェンベースの電子デバイスでは、金が電気接点に一般的に使用されています[6]。したがって、グラフェン-金システムの摩擦は、そのようなグラフェンデバイスの効率的な製造と信頼性の高い動作に重要な役割を果たします。グラフェンは、その優れた機械的特性によりナノトライボロジーの分野の研究者から大きな関心を集めていますが[3、7]、金の表面を滑るグラフェンの摩擦特性はよくわかっていません。これまでのところ、グラフェンの多くのトライボロジー研究は、グラフェンと走査型プローブチップの間の摩擦力に焦点を当てています[8、9、10、11、12、13、14]。たとえば、化学修飾されたグラファイトの摩擦の原子間力顕微鏡（AFM）実験では、負の摩擦係数が明らかになりました[9]。数層グラフェンの摩擦力顕微鏡（FFM）実験では、グラフェン層の数が減少するにつれて摩擦が増加することがわかりました[10、11]。これらの現象は、グラフェンのパッカリング効果によって説明されます[9、10、11]。グラフェンフレークとグラファイトの間の摩擦は、グラファイト上を滑るときに先端がフレークを引きずったときに測定されたと考えられています[8、14]。ラメラ固体のフレークの横方向の動きと結合した回転運動は、フレークが釣り合った構成に再配向するため、摩擦が増加することがわかっています[15]。同時に、他の技術を使用してグラフェンおよび/または金の摩擦を研究することに専念している学者もいます。水晶振動子微量天秤（QCM）技術を使用して、グラフェン上の金の潤滑性[16]と、グラフェン/ Ni（111）基板上の固体キセノン膜の滑り摩擦[17]を研究しました。 QCM実験と分子動力学（MD）シミュレーションの両方で、Au上の不整合なKr単分子層の摩擦が粘性摩擦法則に従うことが示されています[18、19]。 MDシミュレーションは、グラファイト基板上の2次元の金の島と3次元の金のクラスターの静止摩擦を調査するために実施されます[20]。厚いクラスターの有効剛性が高いため、スライダーの厚さが潤滑性を促進できることがわかります。サイズ依存の界面通約可能性は、グラフェンとAu基板上のキセノン原子のMDシミュレーション[21]によっても明らかになり、静止摩擦のサイズ依存性を説明できるCu基板上のクリプトンとシリコンクラスターのシミュレーション[22]と一致します。最近、Au（111）基板上のグラフェンナノリボンの超潤滑性が低温で観察されています[23]。 Kitt etal。 SiO ₂ 上を滑るグラフェンの摩擦を直接測定 基板を作成し、単層および二層グラフェンの摩擦挙動がアモントンの法則に違反していることを発見しました[24]。全体として、純粋な2次元材料として、グラフェンがグラフェン-基板システムに対して非定型の摩擦挙動を示すことを期待するのは合理的です。残念ながら、グラフェンと金属の間の界面特性は体系的に調査されていますが、金基板上でのグラフェンの滑り摩擦の詳細な調査はまだ不足しています[25、26、27、28]。

このギャップを埋めるために、この論文では、単結晶金基板上での可動グラフェンフレークの滑り摩擦挙動を、分子動力学（MD）シミュレーションを使用して徹底的に研究します。フレークサイズ、フレーク形状、フレークと基板間の相対回転角、および基板の結晶配向の影響を調査して、摩擦特性を明らかにします。

メソッド

シミュレーション方法

バネを介して先端に取り付けられたグラフェンフレークが金基板上をスライドするAFM実験をシミュレートするために[29]、 N で作られたグラフェンフレークで構成されるMDモデルを確立します。 原子と単結晶の金の基板。図1を参照してください。基板の下部にある3層の原子は、境界原子として機能するように空間に固定されています。システムの温度を制御するために、基板の境界原子に隣接する4層の原子がサーモスタット原子として選択されます。サーモスタット原子は、速度スケーリング法[30]によって300Kの一定温度に保たれます。この論文では、最初に、スライド中のグラフェンの回転については考慮していません。グラフェン内の原子は、 x 内でのみ移動できます。 および z 方向ですが、 y に制限されています 方向。これにより、シミュレーションが簡略化されます。これがこのホワイトペーパーの主な焦点です。次に、 y でグラフェンの運動制約なしでいくつかのMDシミュレーションをさらに実行します。 実際の実験条件によりよく一致する方向。フレーク原子は、調和ばねを介して一定速度で仮想原子によって引きずられます。基板表面に平行なばねの横方向の剛性は10N / mで、AFMシステムの片持ち梁と先端の頂点の変形を表すために使用されます[31]。シミュレーションでは、一定の法線荷重がフレーク原子に直接適用されます[29、31]。グラフェンフレークは、仮想原子によって10 m / sの一定速度で横方向に引っ張られます。運動方程式は、velocity-Verletアルゴリズムと統合されています。タイムステップは1fsです。 x では境界は周期的です および y 道順、 z で無料 方向。

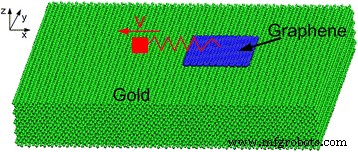
摩擦過程のシミュレーションモデル

基板の結晶配向の影響を調べるために、Au（111）、（001）、（110）面の3つの異なる表面でそれぞれ滑り摩擦のMDシミュレーションを実行します。 Au（111）サーフェスの場合、座標系は\（x- \ left [11 \ overline {2} \ right] \）、\（y- \ left [1 \ overline {1} 0 \ right] \ ）_、 および z -[111]、サイズは19.98×15.0×3.06 nm ³ 。 Au（001）表面の場合、座標系は x と見なされます。 -[100]、 y -[010]、および z- [001]で、基板のサイズは19.99×15.1×3.06 nm ³ 。 Au（110）表面の場合、座標系は x と見なされます。 -[001]、\（y- \ left [1 \ overline {1} 0 \ right] \）_、 および z -[110]、サイズは19.99×15.0×3.03 nm ³ 。 Au（111）、Au（110）、およびAu（001）表面のスライド方向に沿った格子間隔は、それぞれ9.99Å、4.08Å、および4.08Åです。特に記載がない場合は、Au（111）を基板として採用しています。シミュレーションでは、いくつかの異なるフレークのサイズと形状がモデル化されています。デフォルトのフレーク形状は、サイズが5.8 nm（原子数 N ）の正方形です。 =1344）。 x -軸はグラフェンと y のアームチェア方向に沿っています -軸はジグザグ方向に沿っており、 z -グラフェンに垂直な軸。

Au内の原子間力は、埋め込み原子法（EAM）ポテンシャルから導き出されます[32]。 EAMポテンシャルは、さまざまな金属の弾性特性、欠陥形成エネルギー、および破壊メカニズムのモデル化に非常に成功しています[32、33]。また、表面エネルギーや表面再構成などの金属の表面特性を説明するためにもうまく適用されています[32、33、34]。広く使用されているAIREBOポテンシャルは、グラフェン内の原子の相互作用を説明するために適用されます[35]。グラフェンとAu基板間の相互作用は、グラファイト上の金クラスターの摩擦や拡散などの多くの非平衡現象を研究するために使用されてきた標準のレナードジョーンズ（LJ）ポテンシャルによってモデル化されます[36、37]。 LJパラメータ[28、29]は次のとおりです。ε =22.0meVおよびσ =2.74Å。 MDシミュレーションは、大規模な原子/分子の大規模並列シミュレーター（LAMMPS）を使用して実行されます[38]。シミュレーションでは、グラフェンフレークは最初にAu基板表面の上に配置されます。摩擦システムが完全に緩和された後、仮想原子は負の x に沿って滑り始めます。 一定速度の方向。

結果と考察

図2は、さまざまな通常の荷重での滑り距離の関数としての摩擦力を示しています。この論文では、すべり距離は仮想原子のすべり距離です。摩擦力は、AFM実験のようにばねの変形によって測定されます。グラフェンフレークは、1344個の原子からなる5.8nmのサイズの正方形です。摩擦力が継続的に増加し、その後、スティックスリップ運動に典型的な急激な低下が続くことは明らかです。摩擦力の急激な低下はエネルギー散逸につながり、局所的なポテンシャルエネルギーが最小の複数の準安定状態間の遷移の発生を意味します[39]。摩擦力が荷重Lとともに増加することは合理的です。サイズ効果を調べるために、2.0 nm（ N ）のサイズの別の2つの正方形のフレーク =160原子）および10.0 nm（ N =3936原子）を採用しています。スライドプロセス中のさまざまなフレークサイズの摩擦力と平均摩擦力の変化を図3に示します。5.8nmフレークについては、2.0nmと10の両方で明らかなスティックスリップ摩擦も観察できます。 nmフレーク。さらに、原子あたりの平均摩擦力 F には明らかにサイズ効果があります。 _fric / N、図3cを参照してください。同じ荷重の下で、原子あたりの平均摩擦力 F _fric / Nは、フレークが小さいほど大きくなります。このサイズ効果は、フレークサイズの増加に伴う摩擦におけるエッジの役割の漸進的な減少に起因します[40、41]。 QCM実験とMDシミュレーションの両方で、吸着クラスターの摩擦がサイズの増加とともに減少することがわかったことに注意する必要があります[18、19、20、21、22]。これは私たちのシミュレーションと一致しています。ただし、QCM実験とMDシミュレーションにおける摩擦のサイズ依存性は、サイズ依存の界面通約可能性によって説明されます[18、19、20、21、22]。

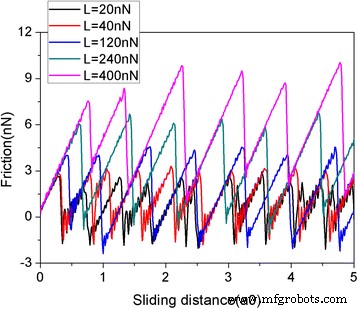
さまざまな垂直荷重（L）での滑り距離の関数としての摩擦力。フレークは5.8nmのサイズの正方形です。ここで、a0（=9.99Å）は、スライド方向に沿ったAu（111）の格子間隔です

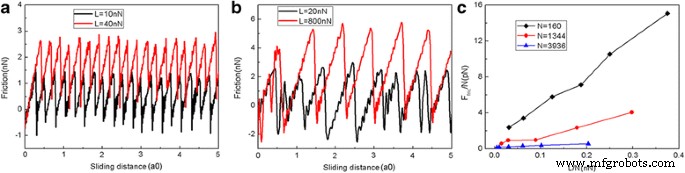
フレークサイズが異なる場合の摩擦力と平均摩擦力の変化。 2.0 nm（ N ）のスライド距離の関数としての一般的な摩擦力 =160原子）フレーク（ a ）および10 nm（ N =3936原子）フレーク（ b ）。 c 原子あたりの平均摩擦力（ F _fric / N）原子あたりの負荷（L / N）の関数として。ここで、a0（=9.99Å）は、スライド方向に沿ったAu（111）の格子間隔です

スライダーの形状は摩擦の決定に重要な役割を果たしているため[42、43]、摩擦プロセスに対するフレーク形状の影響をさらに調査するために、丸いグラフェンフレーク（ N > =1080原子）および三角形のグラフェンフレーク（ N =654原子）。図4は、スライドプロセス中のさまざまなフレーク形状の一般的な摩擦力と平均摩擦力の変化を示しています。図4a、bに示すように、小さな負荷（ L =ラウンドフレークおよび L の場合は20nN =10 nN（三角フレークの場合）、摩擦力はゼロ付近で連続的に変動し、超低摩擦（超潤滑）が観察されます。ただし、通常の負荷が大きい場合（ L =ラウンドフレークおよび L の場合は400nN =三角フレークの場合は200nN）、フレークは明らかなスティックスリップ運動と大きな摩擦力を示します[39]。同じ荷重の下で、原子あたりの平均摩擦力 F _fric / Nは正方形のフレークで最大で、三角形のフレークで最小ですが、 F _fric ラウンドフレークの/ Nはその間にあります。さらに、原子あたりの平均摩擦力の差 F _fric 円形フレークと三角形フレークの間の/ Nはかなり小さいです。しかし、 F _fric 正方形のフレークの/ Nははるかに大きいです。したがって、フレークの形状がスライドプロセスで重要な役割を果たしていることは明らかです。

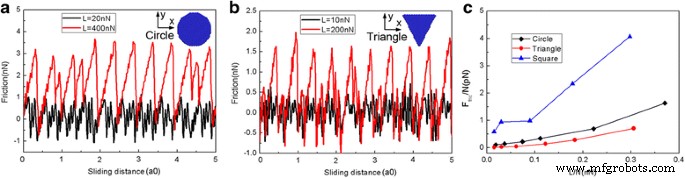
さまざまなフレーク形状の摩擦力と平均摩擦力の変化。ラウンドのスライド距離の関数としての一般的な摩擦力（ N =1080原子）フレーク（ a ）および三角形（ N =654原子）フレーク（ b ）。 c 原子あたりの平均摩擦力（ F _fric / N）原子あたりの負荷（L / N）の関数として。ここで、a0（=9.99Å）は、スライド方向に沿ったAu（111）の格子間隔です

基板に対するフレークの配向も摩擦を決定する上で重要であることはよく知られています[42]。摩擦に対する配向効果を調べるために、グラフェンフレークを z を中心にさまざまな角度で反時計回りに回転させます。 -接点に垂直な軸。回転角0°（回転なし）は、 x の状況に対応します。 -軸はグラフェンのアームチェア方向に沿っており、回転角90°は x の状況に対応しています。 -軸はジグザグ方向に沿っています。 L で回転角が異なる5.8nmの正方形のフレークの滑り距離の関数としての摩擦力の変化 =240nNを図5に示します。対応する平均摩擦力 F _fric さまざまな垂直荷重でのさまざまな回転角について、図6に示すように計算されます。θ=15°およびθ=45°のフレークの場合、摩擦力はゼロ付近で連続的に変動し、超潤滑性が観察されることは明らかです。図6を参照してください。 5b、d。さらに、θ=15°およびθ=45°のフレークの平均摩擦力にはほとんど違いが見られません。図6を参照してください。ただし、θ=30°、60°およびθ=90°のフレークの場合、フレークは明らかなスティックスリップ運動と比較的大きな摩擦力を示します。さらに、θ=30°、60°、およびθ=90°のフレークの回転角が大きいほど、平均摩擦力は大きくなります。回転のあるフレークの摩擦力はすべて、回転のないフレークの摩擦力よりもはるかに小さくなります（θ=0°）。

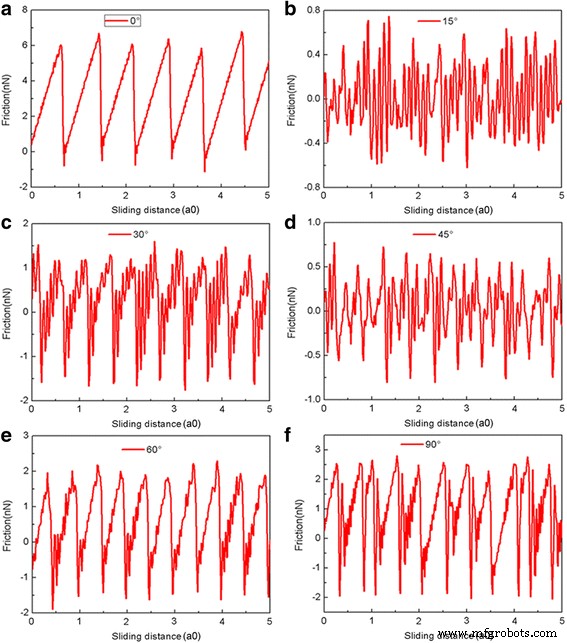
L での5.8nmの正方形のフレークの摩擦力とスライド距離 =240 nN（さまざまな回転角度（θ=0°、15°、30°、45°、60°、90°））。 a – f それぞれ回転角0°〜90°に対応します。ここで、a0（=9.99Å）は、スライド方向に沿ったAu（111）の格子間隔です

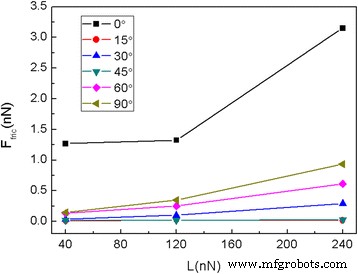
さまざまな垂直荷重でのさまざまな回転角に対する5.8nmの正方形フレークの平均摩擦力Ffric

単結晶金が有意な異方性効果を示すという事実は、摩擦プロセスに対する基板の結晶配向の影響をさらに研究することを私たちに促します。結晶方位と滑り方向のさらに2つの組み合わせ、つまり（001）[100]と（110）[001]のMDシミュレーションを実行しました。摩擦力と平均摩擦力 F _fric 結晶方位の異なるAu基板上を滑る5.8nmの正方形フレークの様子を図1、2に示します。それぞれ7と8。予想通り、摩擦力は通常の荷重で増加します。同じ荷重下で、Au（001）とAu（110）の表面の摩擦力はAu（111）の表面の摩擦力よりも大きく、Au（110）の表面の摩擦力は最大。

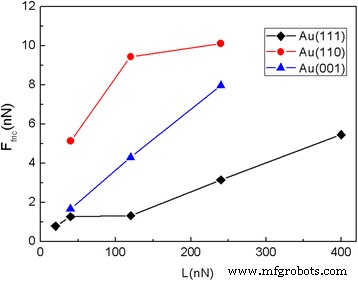
（ a 上を滑る5.8nmの正方形のフレークの摩擦力 ）Au（001）および（ b ）さまざまな垂直荷重でのスライド距離の関数としてのAu（110）表面。ここで、a1（=4.08Å）はスライド方向に沿ったAu（001）の格子間隔であり、a2（=4.08Å）はスライド方向に沿ったAu（110）の格子間隔です

平均摩擦力 F _fric さまざまな通常の負荷でさまざまな結晶方位を持つAu基板上をスライドする5.8nmの正方形のフレークの例

よく知られているPrandtl-Tomlinsonモデル[44]によると、摩擦力は界面エネルギーの波形と密接に関連しています[45,46,47]。摩擦の重要な異方性効果の背後にある根本的なメカニズムを調査するために、フレークの位置を変更したときのフレークとAu基板間の相互作用ポテンシャルエネルギーを計算しました[46]。位置エネルギーは、与えられた荷重の平均高さに対応する固定高さの剛体フレークに対して計算されます[29]。 L でのAu（111）、Au（110）、およびAu（001）表面の位置エネルギーの空間的変化を表す3つの典型的な等高線図 =120 nNをそれぞれ図9a〜cに示します。図9のポテンシャルエネルギー曲面（PES）マップを取得するために、両方の x に沿って21個のメッシュポイントを使用します。 および y 方向。図9では、Au（111）、Au（110）、およびAu（001）について計算されたエネルギー波形は、それぞれ3.5 eV、66.6 eV、および29.1eVです。図9a〜cでは、黒い実線（ y PESマップの=0）は、フレークのスライドパスを示すために使用されます。図9d–fには、Au（111）、Au（110）、Au（001）のスライドパスに沿ったグラフェンと金の相互作用の位置エネルギーもそれぞれプロットされています。図9のAu（111）、Au（110）、およびAu（001）のスライドパスに沿ったエネルギー波形は、それぞれ3.5 eV、59.7 eV、および29.1eVです。エネルギー波形の振幅が摩擦と同じ異方性効果を示していることがはっきりとわかります。 Au（001）およびAu（110）表面のエネルギー波形はAu（111）表面のエネルギー波形よりも大きく、Au（110）表面のエネルギー波形が最大です。したがって、これは、スライドプロセス中の摩擦の重要な異方性効果を明確に説明しています[45、46、47]。グラフェンと基板の相互作用強度（エネルギー波形）の減少に伴って摩擦力が減少するという発見は、MDシミュレーション[16]およびQCM実験[17]と一致しています。

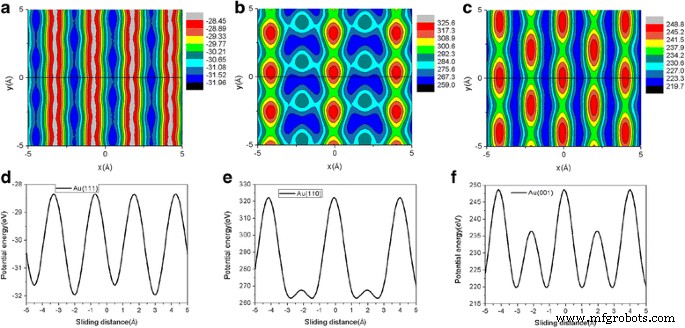
L でのAu（111）、Au（110）、およびAu（001）表面の位置エネルギーの等高線図 =120nNは a に表示されます – c 、 それぞれ。 5.8nm角のグラフェンフレークを採用。 a で – c 、黒い実線（ y マップ上の=0）は、フレークのスライドパスを示すために使用されます。 Au（111）、Au（110）、およびAu（001）表面のスライディングパスに沿ったグラフェン-金相互作用ポテンシャルエネルギーも d にプロットされます。 – f 、 それぞれ。位置エネルギーの単位はeVです。 L でのフレークの平均高さ =Au（111）、Au（110）、およびAu（001）表面の120 nNは、それぞれ2.36Å、2.1Å、および2.17Åです

実際の実験条件によりよく一致させるために、 y でグラフェンの運動制約なしに滑り摩擦のMDシミュレーションをさらに実行しました。 この場合、フレークは y で回転および移動できます。 方向。図10は、1344個の原子からなる5.8 nmの正方形の形状とサイズのグラフェンフレークについて、さまざまな垂直荷重での滑り距離の関数としての摩擦力を示しています。摩擦力の値は変化しましたが、摩擦力は継続的に増加し、その後急激に低下することがわかります。これは、図2と同様の明らかなスティックスリップ運動です。摩擦力は、予想どおり荷重とともに増加します。また、サイズが2.0 nm（ N ）の別の2つの正方形グラフェンフレークの摩擦プロセスについても調査しました。 =160原子）および10.0 nm（ N =3936原子） y のグラフェンの移動制約なし 方向。スライドプロセス中のさまざまなフレークサイズの摩擦力と平均摩擦力の変化を図11に示します。図3と同様に、2.0nmフレークと10nmフレークの両方で明らかなスティックスリップ摩擦も観察されます。さらに、原子あたりの平均摩擦力 F にはサイズ効果があります。 _fric / N、図11cを参照してください。同じ荷重の下で、原子あたりの平均摩擦力 F _fric / Nは、フレークが小さいほど大きくなります。これは、摩擦によるサイズ効果の典型です。全体として、 y を使用した摩擦プロセスのMDシミュレーションの主な結果がわかりました。 - y でグラフェンフレークの運動拘束を緩和した後も、フレーク拘束の方向運動は保持されます。 スライド中の方向。

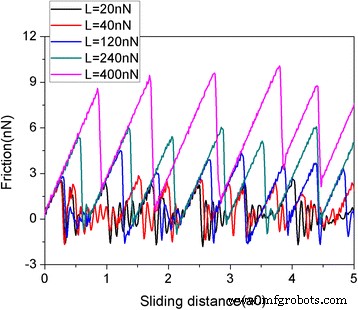
さまざまな通常の荷重（ L ）でのスライド距離の関数としての摩擦力 ） y でのグラフェンの運動制約のない摩擦プロセスの場合 方向。フレークは5.8nmのサイズの正方形です。ここで、a0（=9.99Å）は、スライド方向に沿ったAu（111）の格子間隔です

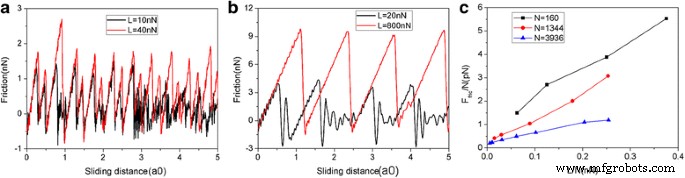
y でのグラフェンの移動制約なしの、摩擦プロセスのさまざまなフレークサイズの摩擦力と平均摩擦力の変化 方向。 2.0 nm（ N ）のスライド距離の関数としての一般的な摩擦力 =160原子）フレーク（ a ）および10 nm（ N =3936原子）フレーク（ b ）。 c 原子あたりの平均摩擦力（ F _fric / N）原子あたりの負荷（L / N）の関数として。ここで、a0（=9.99Å）は、スライド方向に沿ったAu（111）の格子間隔です