フラットバンド材料の計算設計
要約
量子力学は、局所軌道間のホッピング積分がエネルギーバンドを分散させると述べています。ただし、特殊なケースでは、量子干渉による分散のないバンドがあります。これらのバンドはフラットバンドと呼ばれます。フラットバンドを持つ多くのモデルが提案されており、多くの興味深い物理的特性が予測されています。しかし、25年間の精力的な研究にもかかわらず、フラットバンドを持つ実際の化合物はまだ発見されていません。第一原理計算により、一部のパイロクロア酸化物はフェルミ準位のすぐ下に準平坦なバンドを持っていることがわかりました。さらに、それらの価電子帯は、等方性の最近傍ホッピング積分を持つパイロクロア格子の強結合モデルによって十分に説明されています。このモデルは、Mielkeモデルのクラスに属しており、その基底状態は、適切なキャリアドーピングとオンサイトの反発クーロン相互作用により強磁性であることが知られています。また、第一原理から正孔ドープシステムのスピン偏極バンド計算を実行し、基底状態が一部のドーピング領域で強磁性であることを発見しました。興味深いことに、これらの化合物には、遷移金属や希土類元素などの磁性元素は含まれていません。
背景
材料の電子的および磁気的特性は、主にそれらのエネルギー分散によって決定されます。たとえば、価電子帯/伝導帯のエネルギー分散が大きい場合、電子伝導率は高くなります。磁気特性は、バンド分散が小さいときに発生します。通常、バンド分散は原子波動関数の特性によって決定されます。したがって、ほとんどの磁性化合物には、遷移金属元素や希土類元素などの磁性元素が含まれています。磁性元素を含まない磁性体を合成できれば、その影響は計り知れません。
本論文では、第一原理計算を用いて、磁性元素を含まない強磁性体の候補を提案する。非磁性原子の軌道で構成される帯域幅は通常は小さいですが、場合によっては帯域幅が極端に狭くなります。この狭帯域はフラットバンドと呼ばれ、フェルミ準位がこのフラットバンド上にある場合、強磁性基底状態をとることができます。フラットバンド物理学の多くの研究があり、それらは総説[1、2]に要約されています。
本稿では、フラットバンドについて簡単に紹介します。最初に、単純な強束縛(TB)ハミルトニアン\({H} _0 =\ varepsilon \ sum \ Limits_i {c} _i ^ {+} {c} _i + \ sum \ Limits_ {i、j} {t } _ {ij} {c} _i ^ {+} {c} _j \)(1)、ここで c i i の消滅演算子を示します -サイト、ε はオンサイトエネルギーであり、ホッピング積分 t ij は有限で等方性です(= t )サイトが i の場合のみ および j 最近傍にあります。量子力学は、大きなホッピング積分がほとんどの場合大きなエネルギー分散を与えることを示しています。たとえば、 H の場合 0 は単純な正方格子上に定義され、得られるエネルギー分散は E です。 ( k )=ε + 2 t (cos k x + cos k y )。帯域幅 W =8 t 、これは t に比例します 。 t 以降 は原子のような波動関数の重なりによって決定されます。バンドがs軌道またはp軌道で構成されている場合、それは広帯域になります。その場合、スピン整列状態は大きな運動エネルギーを失うため、磁気基底状態は予期されません。
ただし、一部の特定のラティスでは、この単純な関係 W 〜 t 保持しません。たとえば、 H の場合 0 はパイロクロア格子上に定義され、二重に縮退した分散のないバンドが現れます。パイロクロア格子は、パイロクロア構造のAサイト副格子として定義されます。図1を参照してください。このフラットバンドの出現を数学的に証明できます。たとえば、参考文献[3]を参照してください。パイロクロア格子のほかに、2Dチェッカーボード格子、2Dカゴメ格子などのフラットバンドを生成するいくつかの格子があります[1、2]。興味深いことに、このフラットバンドが半分満たされている場合、システムは任意のに対して固有の強磁性基底状態を持っていることを証明できます。 原子内クーロン相互作用の正の値 U [4]。フラットバンドを生成するこのタイプの格子は、局所的なスピン系の言葉で「幾何学的フラストレーション格子」として知られています。実際、一連のパイロクロア酸化物R 2 Ti 2 O 7 (R:希土類元素)は、量子スピン液体、スピンアイス、磁気単極子など、さまざまな新しい磁気特性を持っています[5,6,7,8,9]。最近では、ほぼ完全なフラストレーションが、フラストレーションのあるダイマーマグネットBa 2 で見つかりました。 CoSi 2 O 6 Cl 2 [10]。この化合物の効果的な理論が構築されており、この理論は高磁場における奇妙な磁気特性を説明することができます[11]。
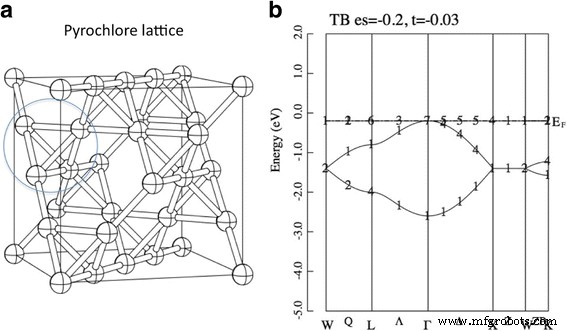
a パイロクロア格子。ボールとスティックは、それぞれサイトとボンドを示します。これは、A 2 のAサイト副格子です。 B 2 O 7 パイロクロア構造。 b パイロクロア格子上の強結合モデル(式1)のバンド分散。パラメータはεとして設定されます =−0.2および t =−0.03。エネルギーの単位はeVです。 ( b の番号 )は既約表現のインデックスを示します。参考文献を参照してください。 [34]
強磁性基底状態に加えて、フラットバンドは超伝導、量子ホール効果、さまざまなトポロジー状態など、いくつかの興味深い特性を誘発することが理論的に示唆されています[12、13、14]。したがって、実際にフラットバンドを持つ化合物を見つけることは非常に重要です。リソグラフィー[15]またはフォトニックラティス[16]を使用してフラットバンドを実現するための理論的な試みがいくつかあります。これらのメゾスコピック材料に加えて、注意深く設計された2Dインジウム-フェニレン有機金属フレームワーク(IPOF)が優れたフラットバンドを示すことに注意してください[17]。興味深いことに、このフラットバンドはトポロジー的に重要であり、高温の分数量子ホール効果のステージとして機能する可能性があります。これらの活発な研究にもかかわらず、おそらくこれらの試みが2Dシステムに限定されているため、期待される磁気長距離秩序はまだ達成されていません。グラフェンに吸収された有機分子によって引き起こされる長距離磁気秩序を示した別の興味深い研究があります[18]。しかし、この磁気秩序の微視的な起源はまだ不明です。
前述のように、このフラットバンドを使用して強磁性を出現させるには、このフラットバンドだけでフェルミ準位を調整する必要があります。ほとんどのパイロクロア酸化物A 2 B 2 O 7 、フェルミ準位はBサイト軌道で構成されるバンド上にあります。ただし、フラットバンドはAサイト副格子(パイロクロア格子)上に形成する必要があるため、Bサイトイオンは不活性である必要があります。さらに、ホッピング積分は等方性である必要があるため、フェルミ準位はAサイトのs軌道上にある必要があります。
上記の条件を課すと、価電子帯の上部にフラットバンドを持つパイロクロア酸化物の候補を選択できます。
$$ \ left(\ mathrm {a} \ right)\ {{\ mathrm {A}} ^ {1 +}} _ 2 {{\ mathrm {B}} ^ {6+}} _ 2 {\ mathrm {O} } _7、\ kern0.75em \ left(\ mathrm {b} \ right)\ {{\ mathrm {A}} ^ {2 +}} _ 2 {{\ mathrm {B}} ^ {5+}} _ 2 { \ mathrm {O}} _ 7、\ kern1em \ left(\ mathrm {c} \ right)\ {{\ mathrm {A}} ^ {3+}} _ 2 {{\ mathrm {B}} ^ {4+} } _2 {\ mathrm {O}} _7。 $$価電子帯の上部にはA-s特性があるため、Aサイトイオンは通常(a)Tl 1+ ; (b)Sn 2+ 、Pb 2+ ;および(c)Bi 3+ 。これらのイオンはすべて(5s) 2 を持っています または(6秒) 2 構成。 Bサイトは不活性である必要があるため、(a)Mo 6+ を選択できます。 、W 6+ ; (b)Nb 5+ 、Ta 5+ ;および(c)Ti 4+ 、Sn 4+ 。これらのBサイトイオンはすべて、閉じたシェル、つまり( n d) 0 または( n p) 0 n の構成 =3、4、5。
上記の組み合わせの中で、3つの化合物に焦点を当てます:
$$ \ left(\ mathrm {a} \ right)\ {\ mathrm {Tl}} _ 2 {\ mathrm {Mo}} _ 2 {\ mathrm {O}} _ 7、\ kern0.75em \ left(\ mathrm {b } \ right)\ {\ mathrm {Sn}} _ 2 {\ mathrm {Nb}} _ 2 {\ mathrm {O}} _ 7、\ kern0.75em \ left(\ mathrm {c} \ right)\ {\ mathrm { Bi}} _ 2 {\ mathrm {Ti}} _ 2 {\ mathrm {O}} _7。 $$化合物(b)Sn 2 Nb 2 O 7 および(c)Bi 2 Ti 2 O 7 すでに合成されている[19,20,21,22,23]が、(a)Tl 2 Mo 2 O 7 まだ報告されていません。ただし、類似のパイロクロア酸化物T1 2 Ru 2 O 7 すでに合成されており、独特の金属-絶縁体転移を示しています[24]。 MoとRuの原子半径は類似しているため、Tl 2 Mo 2 O 7 特定の条件で合成することができます。興味深いことに、両方(b)Sn 2 Nb 2 O 7 および(c)Bi 2 Ti 2 O 7 光触媒材料の候補として知られています。
これらの化合物の第一原理計算を実行しました。この論文は次のように構成されています。「方法」のセクションでは、計算方法と計算した結晶構造について説明します。 「結果と考察」のセクションでは、計算結果を示し、いくつかの議論を行います。要約は「結論」セクションで説明されています。
メソッド
Tl 2 の電子構造を計算しました Mo 2 O 7 、Sn 2 Nb 2 O 7 およびBi 2 Ti 2 O 7 第一原理から。簡単にするために、それらはすべて理想的なA 2 を持っていると仮定しました B 2 O 6 O 'パイロクロア構造。 2つの酸素サイトがあるので、それらを区別するためにOとO 'と呼びます。全ポテンシャル拡張平面波(FLAPW)スキームを使用し、交換相関ポテンシャルは一般的な勾配近似内で構築されました[25]。コンピュータプログラムWIEN2kパッケージ[26]を使用しました。パラメータ RK max 7.0として選択されます。 k -ポイントメッシュは、最初のブリルアンゾーンのメッシュの総数が〜1000になるように取得されます。また、空間群の対称性を固定して、結晶構造を最適化しました。 A 2 の結晶構造 B 2 O 6 O 'は次のとおりです。空間群Fd-3m(#227)、A(0,0,0)、B(1 / 2,1 / 2,1 / 2)、O( x 、0,0)、およびO '(1 / 8,1 / 8,1 / 8)。 Sn 2 の場合 Nb 2 O 7 およびBi 2 Ti 2 O 7 、実験的な格子定数を使用しました。 Tl 2 の場合 Mo 2 O 7 、格子定数も最適化しました( a )および取得した a =10.517Å。これは、類似化合物Tl 2 の最近の実験的格子定数に非常に近い値です。 Ru 2 O 7 [27]。この構造では、唯一の自由パラメーターはOの位置です(= x )。原子位置の収束は、1.0 mRy /a.u未満の各原子に作用する力によって判断されます。
結果と考察
バンド構造
図2は、Tl 2 のエネルギーバンド分散を示しています。 Mo 2 O 7 、Sn 2 Nb 2 O 7 およびBi 2 Ti 2 O 7 第一原理から。まず、中央のパネルであるSn 2 に注目します。 Nb 2 O 7 。得られたバンド分散は以前の研究とよく一致していますが、準フラットバンドの存在については言及されていません[19、28]。価電子帯の上部の形状(− 3〜0 eV)は、図1bに示す強結合モデルに類似していることがわかります。このモデルは2つのパラメーターεのみを使用するため、この合意はかなり驚くべきものです。 および t 。したがって、最初の近似として、Sn 2 の価電子帯 Nb 2 O 7 「Sn-s」軌道からなるTBバンドで表されます。ここで、これらの「Sn-s」軌道は、Sn-s軌道とO'-p軌道からなる反結合性軌道であることに注意してください。 ab-initioバンドとTBバンドの主な違いは、エネルギー〜0 eVでのバンドの平坦性です。つまり、ab-initioバンドを正確に適合させるには、最近傍のSn原子以外のホッピング積分も必要です。 。
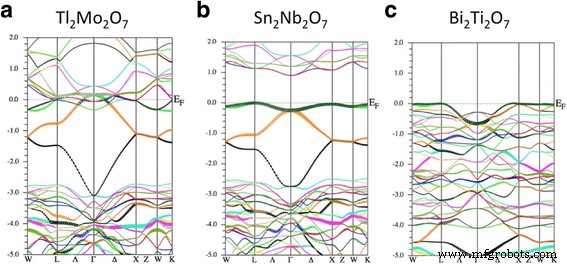
( a の電子バンド構造 )Tl 2 Mo 2 O 7 、( b )Sn 2 Nb 2 O 7 、および( c )Bi 2 Ti 2 O 7 。エネルギーの単位はeVです。
次に、Tl 2 のバンド構造について説明します。 Mo 2 O 7 、図2の左側のパネルに示されています。Tl 2 の価電子帯の形状がわかります。 Mo 2 O 7 Sn 2 とほぼ同じです Nb 2 O 7 、Tl 2 にフラットバンドが存在することを示します Mo 2 O 7 。しかし、伝導帯はそのエネルギーを低下させ、バンドギャップは崩壊します。 Sn 2 の場合とは異なり、Mo-dバンドは部分的に占有されています。 Nb 2 O 7 、正式なイオン配置Tl 1+ 2 Mo 6+ 2 O 2- 7 適切ではありません。この結果は、点電荷モデルによる分析が非常に効果的であることを示唆しており、A 1+ 2 B 6+ 2 O 7 パイロクロア酸化物の安定した構成ではありません。 Tl-sフラットバンドは、類似のパイロクロア酸化物Tl 2 の場合と同様に、Mo-dバンドと絡み合っています。 Ru 2 O 7 [29]。金属-絶縁体転移はTl 2 に見られます Ru 2 O 7 その原因は隠されたTl-sフラットバンドに起因します[30]。この金属-絶縁体転移はTl 2 でも起こると予想できます。 Mo 2 O 7 合成された場合。
最後に、Bi 2 のバンド構造について説明します。 Ti 2 O 7 、図2の右側のパネルに示されています。得られたバンド分散は、以前の研究[31]とよく一致しています。 Bi 2 間の価電子帯の形状が異なるにもかかわらず Ti 2 O 7 およびSn 2 Nb 2 O 7 、Bi 2 の価電子帯の上部 Ti 2 O 7 ブリュアンゾーンの対称軸のほとんどの部分で非常に平坦です。バンドの形状が図1とは異なるため、この部分的な準フラットバンドの起源は、パイロクロア格子のフラットバンドに単純に見つけることはできません。それにもかかわらず、準フラットバンドとその結果生じる高密度状態密度(DOS)は、正孔をドーピングするときに強磁性の実現を期待するのに十分です。この点については、次のサブセクションで説明します。
強磁性状態
前のサブセクションでは、Sn 2 の価電子帯の上部に準平坦なバンドが見つかりました。 Nb 2 O 7 。 Bi 2 の場合 Ti 2 O 7 、部分的な準フラットバンドも見つかりました。それらは絶縁体であるため、強磁性を誘発するために準フラットバンドに穴を導入する必要があります。完璧なフラットバンドの場合、 any オンサイトクーロン相互作用の値 U フラットバンドが半分満たされると、強磁性基底状態を引き起こします[4]。これは、十分に拡張された原子のs軌道またはp軌道でさえ、強磁性基底状態を引き起こす可能性があることを意味します。準フラットバンドの場合については、数値研究により、ある大きな U > U c U の場合、強磁性を誘発する可能性があります c は臨界値であり、 U c 帯域幅のオーダーは W [32]。 U の推定以来 および U c 実際の化合物では困難ですが、代わりにスピン偏極したab-initio計算を実行しました。バンド計算も狭帯域を持つbccFeの強磁性基底状態を記述するのに成功していることを考えると、我々のアプローチは正当化されるでしょう。正孔ドーピングをシミュレートするために、O 'の代わりにNを使用します。つまり、Sn 2 を計算しました。 Nb 2 O 6 NとBi 2 Ti 2 O 6 N.この置換により、プリミティブユニットセルごとに2つの電子(式単位ごとに1つの電子)が減少するため、準フラットバンドは半分満たされます。
図3は、Sn 2 のDOS曲線を示しています。 Nb 2 O 6 NとBi 2 Ti 2 O 6 N.上記の準フラットバンドは、フェルミ準位のすぐ近くに鋭いピークを形成します。両方の化合物が半金属になる、つまりエネルギー E を持つ電子のスピン状態になることがわかります。 = E F (フェルミエネルギー)は完全に分極しています。総磁気モーメント M は2.00μ B 両方の化合物のプリミティブユニットセルあたり。これは、伝導電子が完全にスピン偏極していることも示しています。アップスピンバンドとダウンスピンバンドの間の交換分割は、Sn 2 の場合〜0.3eVです。 Nb 2 O 6 Bi 2 の場合はNおよび〜0.4 eV Ti 2 O 6 N.これらの値は、bcc Feの交換分割よりもはるかに小さく、〜2eVです。交換分割は原子波動関数[33]によってほぼ決定されるため、dバンドはsバンドまたはpバンドよりも大きな交換分割を持ちます。それにもかかわらず、Sn 2 Nb 2 O 6 NとBi 2 Ti 2 O 6 Nの帯域幅は非常に小さく、交換分割は帯域幅を超え、ハーフメタリック基底状態が実現します。
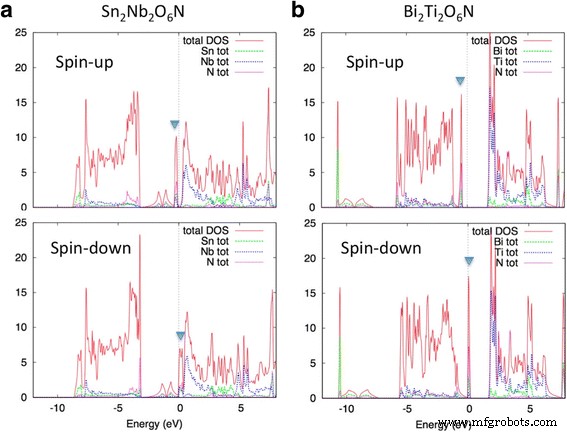
( a のDOS曲線 )Sn 2 Nb 2 O 6 Nと( b )Bi 2 Ti 2 O 6 スピン偏極状態の場合はN。塗りつぶされた三角形は、準フラットバンドの位置を示しています
結論
この論文では、フラットバンドコンパウンドを設計するための指針を示しました。この原理に従って、3つのパイロクロア酸化物を選択し、第一原理研究によってそれらの電子構造を調査しました。強結合分析と組み合わせると、一部の化合物が実際に準フラットバンドを持っていることがわかりました。また、これらの化合物には磁性元素が含まれていないにもかかわらず、これらの化合物への正孔ドーピングが強磁性基底状態につながることもわかりました。これらの発見は、化合物のフラットバンドシステムだけでなく、磁性元素を含まない強磁性体を実現するための大きな一歩となるでしょう。
略語
- DOS:
-
状態密度
- FLAPW:
-
全ポテンシャル増強平面波
- TB:
-
タイトバインディング
ナノマテリアル



