単結晶シリコンのハイブリッド加工プロセスにおける切削機構の分子動力学シミュレーション

はじめに

単結晶シリコンは重要な半導体材料であり、その優れた光学的および機械的特性により、赤外線光学、マイクロエレクトロニクス、およびオプトエレクトロニクスシステムで広く使用されています[1、2]。ただし、単結晶シリコンの硬度と脆性の性質により、機械加工中に微視的な脆性破壊と表面下の損傷が発生する可能性があります。マイクロフライス盤加工では、加工物に加工による内部型エッジチッピング不良が発生する場合があります[3]。単結晶ダイヤモンドカッティング（SPDT）加工では、処理パラメータに応じて200〜600 nmの範囲の損傷層が形成される可能性があります[4、5]。ただし、表面下の損傷層は、研削と研磨によって約50nmまで減らすことができます。複雑な構造を製造する際の加工効率と能力には限界があります。これらの問題を克服するために、さまざまな補助加工技術が提案され、テストされてきました。特に、熱アシスト切断（TAC）[6]と振動アシスト切断（VAC）[7]は、その並外れた切断性能として広く注目されています。

単結晶シリコンのような脆性材料の場合、加工温度を上げると、脆性から延性への遷移が促進されます。 TACプロセス中、シリコンワークピースは熱的に軟化するため、切削抵抗[8]と比切削エネルギー[9、10]が低下します。一方、高圧相の立方晶シリコン相へのアニーリングは、加工温度を上げると明らかになります[11]。加工パラメータを適切に選択することで、TACによって、相純度が高く、表面下の損傷が少ない、目的の加工面を実現できます[12、13、14]。 TACに加えて、振動アシストカッティング（VAC）は、単結晶シリコン上に高品質の表面を実現するためのもう1つの促進方法です。この技術は、1960年代から製造業に適用されてきました[15]。この技術の初期の開発では、公称切削方向の線形振動運動のみが機械加工で実行されます。これは線形振動切削（LVC）と呼ばれます。 1994年に、楕円振動切断（EVC）がShamotoとMoriwakiによって提案されました[16]。以下のように、シリコン[17、18]、反応結合炭化ケイ素[7]、炭化タングステン[19、20]、硬化鋼[21]などの多くの脆性材料でのEVCの加工可能性が検証されています。 EVCプロセス中は、一時的な切込み深さ（DOC）が公称DOCよりもはるかに小さいため、表面下の損傷を効果的に抑制することができます[22]。また、振動サイクルごとに分離しているため、切削工具とワークの接触面が周囲のガスや流体にさらされ、発生した切削熱を放散します。したがって、接着や熱化学反応[23]などの切削工具の摩耗を効果的に抑制することができます。

脆性材料の被削性をさらに向上させるために、熱と振動の補助を組み合わせたハイブリッド加工（HM）実験が実施されました[24、25]。インコネル718をHM法で切削すると、加工面の粗さを効果的に低減できることがわかりました[26]。実験と有限要素法（FEM）シミュレーションにより、HMプロセス中に切削抵抗の大幅な低下とチタン合金の優れた表面品質を実現できます[27]。これらの結果は、脆性材料の精密機械加工におけるHM法の実現可能性を示しています。しかし、切削工具は高周波で振動し、変形ゾーンは高温であるため、機械加工プロセス中の物理的変数を直接観察および測定することは困難です。さらに、ナノメートルの表面製造では、一時的な材料除去の厚さは通常、サブナノメートルから数ナノメートルの範囲です。したがって、量子力学的効果が明らかになるため、FEMなどの問題の従来の連続体表現には疑問があります。

近年、分子動力学（MD）シミュレーションは、ナノメートル切削プロセスの研究における利点のために、補助機械加工プロセスの研究に広く適用されています[28、29、30]。以前のTACのシミュレーション[31]に基づくと、切削温度を上げると、切削抵抗、比切削エネルギー、および降伏応力の異方性がより明確になります。一方、ワークピースのせん断力は、切削温度が高くなるほど低くなり、せん断ゾーンが狭くなり、せん断面角度の大きさが大きくなります[32]。さらに、より多くの切りくずが形成されるため、切削温度を上げると材料除去率を向上させることができます[33]。 EVCプロセスでは、MDシミュレーションにより、変形領域の圧縮応力とせん断応力を通常の切削に比べて大幅に低減できることがわかりました[34]。これは地下損傷の抑制に有利です。その上、EVCプロセスは切削切りくずの明らかな薄化を示し、その結果、切削切りくずの厚さに対する未切削の切りくずの厚さの比率が増加します[35]。さらに、振幅比、振動周波数、位相差などの振動パラメータが材料除去性能に大きな影響を与えることが解明されています[34、36]。

これらの目覚ましい成果により、補助加工プロセスの加工メカニズムの理解が深まりました。ただし、計算時間とメモリを節約するために、シミュレーションシステムは通常非常に小さいです。 EVCプロセスの以前のシミュレーションでは、振動振幅と公称DOCは5 nm未満です[22、36]。したがって、一時的な材料除去の厚さは通常1 nm未満であり、実際の材料除去プロセスを正確に表すことはできません。さらに、HMプロセスのMDシミュレーションは報告されていません。 HMプロセス中の材料除去プロセスと地下損傷形成のメカニズムはまだ不明です。そこで本論文では、HMプロセスの切削メカニズムを明らかにするためにMDシミュレーションを実施した。従来の切削モデルは、振動パラメータが実験値に非常に近くなるように変更されています。たとえば、振動振幅は、公称切削速度3.125 m / sで40nmに拡大されています。 1回の振動サイクルでの材料除去メカニズムと切削温度の上昇の影響を調査します。 MDシミュレーションは、有名な大規模原子/分子大規模並列シミュレーター（LAMMPS）によって実行されます[37]。シミュレーション結果の分析には、後処理ソフトウェアOVITO [38]を採用しています。

シミュレーション方法

カッティングモデルの詳細

図1は、元々Shamoto etalによって提示されたEVCプロセスの概略図を示しています。 [39]。ツールの軌道は次のように表すことができます：

ここで x （ t ）および z （ t ） x で切削工具の変位を表します および z 方向。 A _c および A _d は、公称切削方向（ x ）の振動振幅です。 方向）および公称DOC方向（負の z 方向）。パラメータ f 、 v 、φ 、および t それぞれ、振動周波数、公称切削速度、位相差、およびシミュレーション時間を表します。シミュレーション時間 t _i ポイント P の時間を表します _i 図1の工具軌道上。

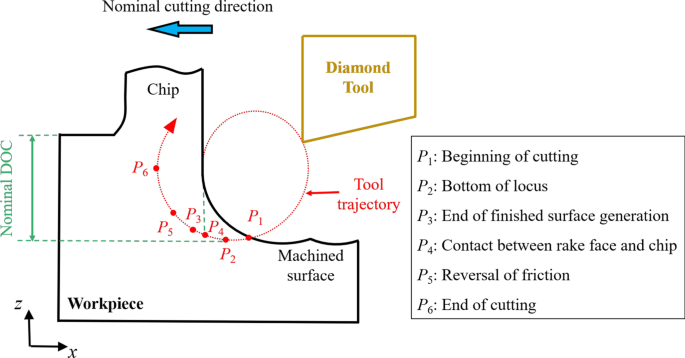
EVCプロセスの概略図

幾何学的関係[40]によると、 t の値 ₁ および t ₃ によって決定することができます：

次に、 t ₆ ダイヤモンド工具の過渡移動方向が工具すくい面に平行な場合に得られます：

ここで、γ はダイヤモンド切削工具のすくい角です。

MDモデルを図2に示します。単結晶シリコンワークピースは変形可能なボディとして設定されています。このシミュレーションでは工具の摩耗を無視できるため、ダイヤモンド工具は剛体と見なされます。従来の切削モデルのワークの形態は、工具のエッジ半径を考慮して、前の振動サイクルでの工具の軌道に従って再形成されます。ツールの軌道は、図2bに示すように決定できます。 P _o および P _b ツールエッジ円の中心と下端です。ツールエッジ効果を考慮すると、過渡的な表面生成ポイント P _c ツールの移動中にツールのエッジに沿って変化します。実際の仕上げ面は、切削工具エッジのエンベロープラインによって生成されます。 P の軌道の場合 _b 式で表されます。 （1）と（2）、 P の軌道 _c [41]で計算できます：

ここで

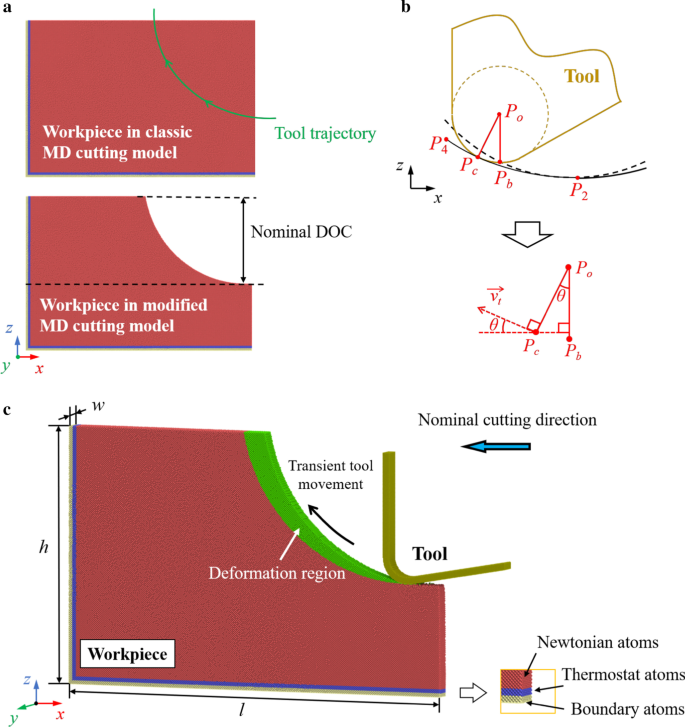
MDカッティングモデルのスキーム。 a ワークピースの変更。 b ツールの軌道の決定。 c 修正されたMDモデルの形態。緑の原子は、1つの振動サイクルの変形領域を表します

シリコン原子は、境界原子、サーモスタット原子、ニュートン原子の3つのグループに分けられます。境界原子は、シミュレーション中にワークピースを保持するためにバランスの取れた位置に固定されています。サーモスタット原子は周囲温度に保たれ、発生した切削熱を放散しますが、ニュートン原子はニュートンの第2法則に従います。

シミュレーションパラメータの詳細を表1に示します。長さ l と高さ h カッティングゾーンと固定境界の間に十分な距離を保つように決定されました。周期境界条件は y に沿って適用されます バルクシリコンを模倣する方向。公称切削方向、工具すくい角/逃げ角、および位相差は、実験のセットアップを参照して決定されました[42]。振動振幅と公称DOCは、許容可能なシミュレーションコストで実験スケールに近づくように拡大されます。一方、除去された材料（図2cの緑色の原子）の厚さを確保するために、速度比と振動周波数はそれぞれ40MHzと500MHzに設定されました。したがって、公称切削速度は3.125 m / sと決定されました。さらに、切削温度の異なるシミュレーションを実施して、切削メカニズムに対するサーマルアシスタントの効果を明らかにします。切削温度は300から1200Kに上昇します。これは、レーザー加工のようなTAC中に実現可能です[4、11]。

この修正モデルでは、振動サイクル中の切削段階のみがシミュレートされ、ワー​​クピースが切削工具で分離されるときのタイムステップが保存されます。したがって、計算能力を過渡切削プロセスに集中させることができます。最も重要なことは、一時的な材料除去プロセスを正確に説明できることです。変更されたモデルと従来のMDモデルの比較を表2に示します。

潜在的な機能

MDシミュレーションでは、原子間の相互作用を記述するためにロバストなポテンシャルを採用することが重要です。単結晶シリコンの場合、学者は、修正された埋め込み原子法（MEAM）[45]、Stillinger–Weber（SW）[46]、Tersoff [47]、電荷最適化多体（COMB）[COMB）などの多くの可能性を開発しました。 48]ポテンシャル。これらのポテンシャルの中で、Erhart and Albe [49]によって提案された分析的結合次数ポテンシャル（ABOP）がますます注目を集めています。これは、機械加工シミュレーション中に結合の形成と切断を可能にする3体のポテンシャル関数です。以前の研究[50]によると、ABOPはシリコンの二量体とバルクの両方の特性を正確に記述することができます。一方、ABOPによって製造されたシリコンの機械的特性は実験とよく一致しており[31]、これはナノスケール機械加工のMDシミュレーションで重要です。したがって、この論文では、ABOPポテンシャルを適用してシリコン-シリコンおよび炭素-炭素相互作用を説明します。一方、シリコンと炭素の相互作用は、ナノスケールの切削シミュレーションで効率的なポテンシャルとして証明されているモースポテンシャルによって記述されます[51、52]。モースポテンシャル関数は次のように表すことができます。

ここで D _M 、a、 および R _M は、凝集エネルギー、弾性率、および原子間の平衡距離をそれぞれ表します。モースポテンシャルのパラメータは[53]： D _M =0.435 eV、 a =46.487 nm ^-1 、 R _M =0.19475nm。

結果と考察

切断性能

通常の切削では、主要な材料除去メカニズムは、変形していない切りくずの厚さによって大きく影響を受ける可能性があります[54]。変形していないチップの厚さが小さい場合、主要な材料除去メカニズムは押し出しです。金属安定相（Si-II）は、シリコンの延性変形を促進する高圧相転移（HPPT）によって生成できます。変形していない切りくずの厚さが増すと、材料は主にせん断プロセスによって除去できます。 EVCプロセスでは、変形していないチップの厚さが絶えず変化するため、材料除去メカニズムは1回の振動サイクルで押し出しからせん断に変化します。図3は、300 Kでの切削シミュレーションのスナップショットを示しています。ワークピースの結晶構造は、Common Neighbor Analysis（CNA）[55]によって決定されます。この分析では、立方晶または六角形のダイヤモンド格子に配置された原子が見つかります。図3c、eの非ダイヤモンド構造には、主にアモルファス相（a-Si）、Si-II、およびその他の欠陥原子が含まれています[56]。これらの構造は不安定であり、切断後にa-Siに変化します。図3b、cから、材料は主に初期の切断段階で押し出しによって除去されることがわかります。切削工具のエッジの近くに一時的なよどみ点が見られます。通常の切削と同様に、変形領域の材料はよどみ点によってチップと圧縮材料に分割されます。切削工具が進むにつれて、変形していない切りくずの厚さが増加します。せん断面と多結晶粒子がワークピースに生成され、せん断が主要な材料除去メカニズムになることを示しています。

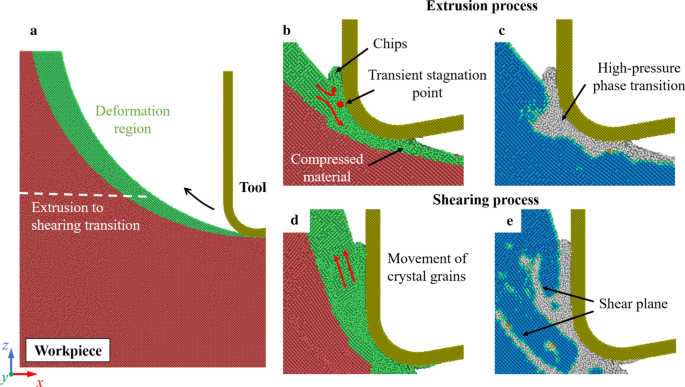
材料除去メカニズムの移行。 a 変形領域の図。 b 、 d 押し出しおよびせん断プロセス。 c 、 e ワークピースの結晶構造の識別。青い原子は立方体のダイアモンド構造を表し、灰色の原子は非ダイアモンド構造になっています

図4は、さまざまな切削温度でのワークピースの形態を示しています。 300 Kでは、工具を上向きに動かしているときに、ワークピースに明らかな亀裂と破壊が見られます。単結晶シリコンのような脆い材料の場合、工具を上に動かすと材料が剥がれ、ワークピースに欠陥が残ります。これは、EVCの特定の問題と見なされています[42]。これらの亀裂は、さらなる振動サイクルによって除去できますが、ワークピースの表面の不規則性により、加工安定性に影響を与えます。切削温度を上げると、クラックの発生や伝播を効果的に抑制します。図4dから、切削温度が1200 Kに上昇しても明らかな破壊は検出されません。ただし、900Kおよび1200Kでは、材料除去メカニズムがせん断に変化すると、加工面の膨張が明らかになることが観察されます。せん断段階でより多くの結晶粒が生成されると、高温でのこれらの結晶粒の回転によって膨潤が引き起こされる可能性があると結論付けることができます。

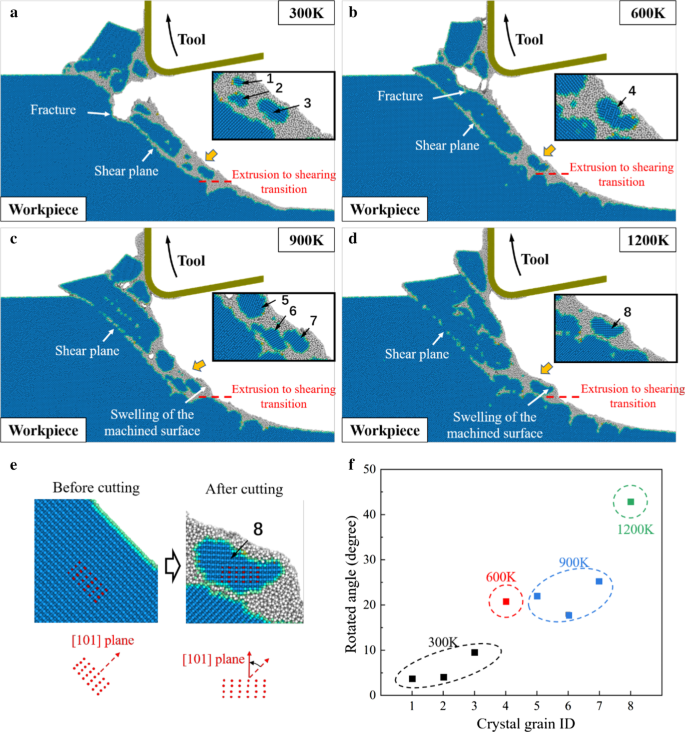
a でのHMプロセスのワークピースの形態 300 K. b 600 K. c 900 K. d 1200 K.青色の原子は立方体のダイアモンド構造を表し、灰色の原子は非ダイアモンド構造を表します。 e 結晶粒の回転角の決定。 f 切削温度の上昇に伴う回転角

この回転を明確に説明するために、図4eに示すように、結晶粒子内の24個のマークされた原子（赤い原子）の座標を使用して、平均回転角を計算します。 8つの結晶粒（図4a〜dで番号が付けられている）の回転角度は、図4fに要約されています。回転角は高温で明らかに増加することが観察できます。 HMプロセス中、a-Siの粘度は高温で大幅に低下する可能性があり、工具の上方への移動によってワークピース原子の引き上げ運動が促進されます。したがって、ワークピース内の原子の流れが促進され、結晶粒の回転が促進され、加工面の膨潤につながる。結晶粒の回転を抑えるために、ワークの過熱を防ぐために加熱力を制御する必要があります。さらに、振動パラメータは慎重に選択する必要があります。たとえば、結晶粒の生成を抑制し、さらなる振動サイクルによる膨張を除去するために、より小さな公称切削速度とより高い振動周波数を適用する必要があります。図5に示すように、適切な振動パラメータを使用して、 P ₁ 押し出し段階で位置を特定でき、最終的な機械加工面は、膨潤することなく押し出しによって生成されます。

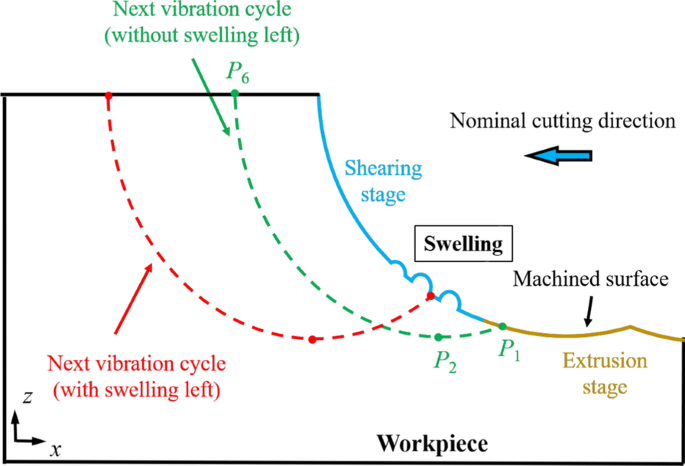
HMプロセスでの腫れの解消

ワークピースの応力フィールド

HMプロセス中の切削メカニズムをさらに調査するために、ワークピースの応力分布を計算しました。 MDシミュレーションでは、静水圧応力は次のように表すことができます。

ここで、σ _x 、σ _y 、およびσ _z 、はLAMMPS出力データからの応力テンソルです。

押し出しおよびせん断段階での静水圧応力分布を図6に示します。また、圧縮領域と引張領域の応力のピーク値をマークしました。工具の動きに伴い、工具とワークピースの接触点は工具のエッジサイクルに沿って変化し、その結果、圧縮領域が工具のエッジからすくい面に移動します。以前の報告に続いて、単結晶シリコン相（Si-I）からSi-IIへのHPPTは、10〜12 GPaから始まる圧力で発生する可能性があります[57、58]。 300 Kでの切削シミュレーションでは、押し出し段階とせん断段階での最大圧縮応力は、それぞれ18.1GPaと17.6GPaに達しました。この結果は、延性のあるSi-II相が切断中に生成される可能性があり、HPPTがまだせん断段階に存在することを示しています。また、押出段階では、シリコン原子と工具表面の付着により、主に工具逃げ面と加工面の接触部付近に引張応力が集中します。工具がせん断段階に進むと、引張領域が拡大し、引き上げ動作によって引き起こされる表面下のワークピースの引張応力集中が大幅に増加します。切削温度を上げると、単結晶シリコンの塑性変形能が向上し、ワークの内部応力が減少します。温度が300Kから1200Kに上昇すると、最大圧縮応力は、押し出しおよびせん断段階で16.6％および25％減少しました。一方、表面下のワークピースの引張応力集中は依然として明らかですが、引張応力のピーク値は明らかに30％以上減少しています。単結晶シリコンの破壊靭性は、高温で効果的に増加できることが報告されています[59]。そのため、工具の上方への移動による引き剥がし効果によるひび割れや破損を効果的に抑えることができます。

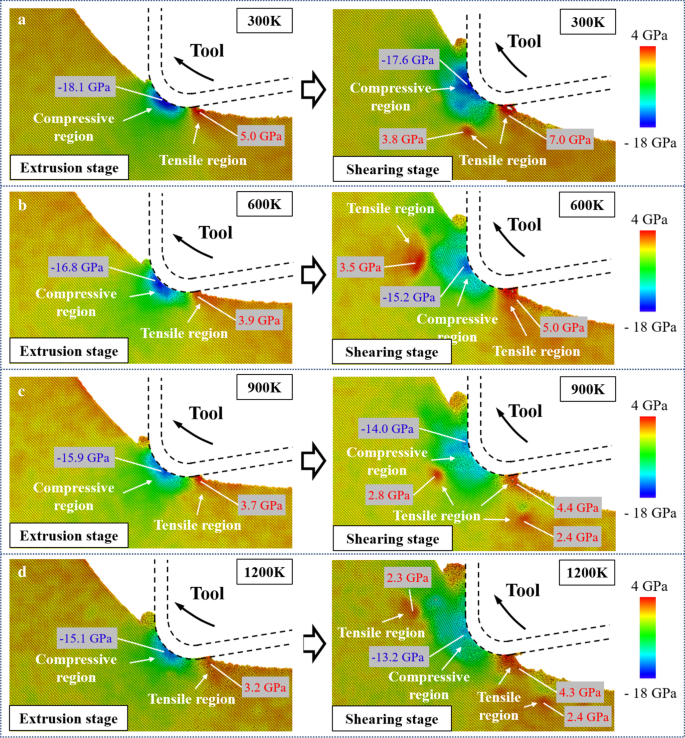
a での静水圧応力分布 300 K. b 600 K. c 900 K. d 1200 K

単結晶シリコンは、12個のすべり系を備えた面心立方（FCC）結晶構造を持っています。ツールの動きに基づくと、せん断変形の主なすべりシステムは、（111）/ [\（\ stackrel {\ mathrm {-}} {1} \）01]と（1 \（\ stackrel {\ mathrm {- }} {1} \）1）/ [\（\ stackrel {\ mathrm {-}} {1} \）01]システム。したがって、分解されたせん断応力成分τ _s （111）/ [\（\ stackrel {\ mathrm {-}} {1} \）01]でスリップシステムが計算されます。図7に示すように、分解されたせん断応力成分τ _s M の方向に すべり面の N 応力テンソルを介して次のように計算できます：

ここで a ₁ 、 b ₁ 、 c ₁ 平面の法線方向の方向余弦 N a ₂ 、 b ₂ 、 c ₂ スリップ方向の方向余弦です M 。 τの間 _xy 、τ _xz 、およびτ _yz LAMMPS出力データからのせん断応力テンソルです。

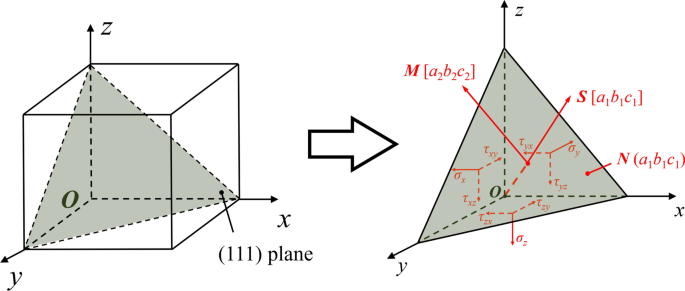
応力テンソルの図

分解されたせん断応力の分布τ _s を図8に示します。τが正の領域 _s [\（\ stackrel {\ mathrm {-}} {1} \）01]方向に沿ったすべり運動が促進されるため、せん断領域として定義されます。これにより、せん断による材料の除去が容易になります。一方、τが負の領域 _s 反対方向のすべり運動が好ましく、ワークに表面下損傷が発生するため、損傷領域とみなします。押し出し段階では、せん断領域の応力は損傷領域の応力よりも小さくなります。せん断変形によって引き起こされる表面下の損傷は、機械加工された表面の下で発生する可能性があります[60]。切削工具の動きに伴い、[\（\ stackrel {\ mathrm {-}} {1} \）01]方向に沿ったせん断応力が徐々に増加し、材料の除去が押し出しからせん断に移行します。また、損傷領域の位置が工具の動きに沿って上方に移動するため、発生した損傷は、さらなる振動サイクルによって除去でき、ワークピースに残りません。温度が300Kから1200Kに上昇すると、損傷領域のせん断応力は、押し出し段階とせん断段階でそれぞれ36.1％と42.4％減少しました。対照的に、ツールの上方への動きにより、せん断段階での[\（\ stackrel {\ mathrm {-}} {1} \）01]方向に沿ったせん断応力の減少はそれほど明白ではありません。すべり運動の臨界分解せん断応力（CRSS）は、[61]：

ここで U とεは、グライド運動の活性化エネルギーとひずみ速度を表します。パラメータ n および C 材料定数です。 CRSSは、温度の上昇とともに明らかに減少する可能性があると結論付けることができます。したがって、[\（{\ overline {\ text {1}}} \）01]方向のせん断変形は、高温で促進されます。

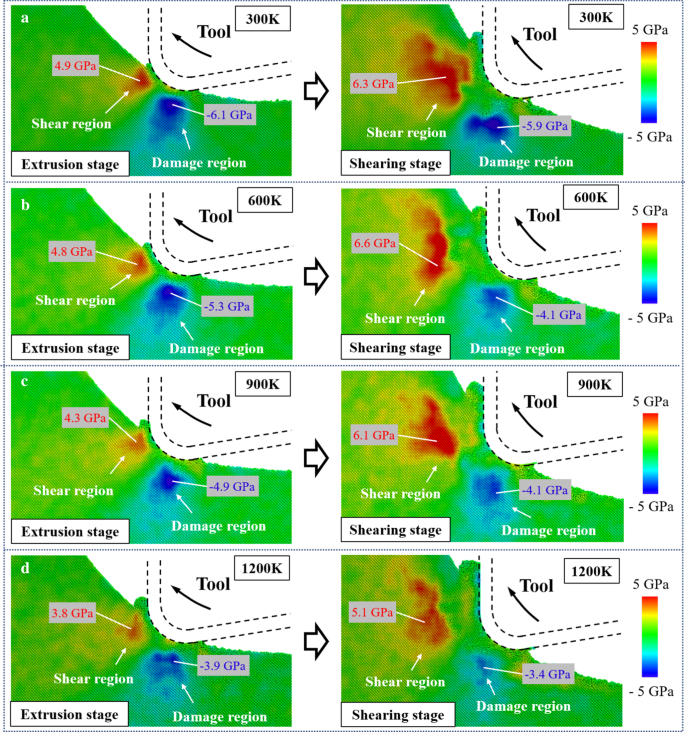
a での分解されたせん断応力分布 300 K. b 600 K. c 900 K. d 1200 K

相転移

切削温度を上げると、シリコンの相転移に大きな影響を与える可能性があります。 a-Siの緩和とSi-Iへの遷移は、適切な温度で促進することができます[62]。図4では、高温になるとワークの損傷パターンが狭くなります。 1200Kで切断したときの損傷パターンの詳細な観察結果を図9aに示します。変形領域で発生した損傷は、切断後に部分的に回復していることが観察され、非ダイヤモンド構造からSi-Iへの遷移が発生したことを示しています。また、図9bに示すように、切削温度を上げると、より多くのSi-I原子が生成されます。さらに、1200 Kで加工されたワークピースの構築された表面メッシュ（赤色）[63]が図9cに示されています。表面下のワークピースにいくつかの空孔が形成されていることが観察されます。原子はSi-I相でより密に詰まっているため、Si-Iへの遷移により材料が収縮し、ワークピースに空孔が生じる可能性があります。さまざまな温度での空孔の体積が計算され、図9dに示されています。室温ではほとんど空孔が発生しないことが観察されます。切削温度が900Kと1200Kに上昇すると、空孔の明らかな増加を検出できます。

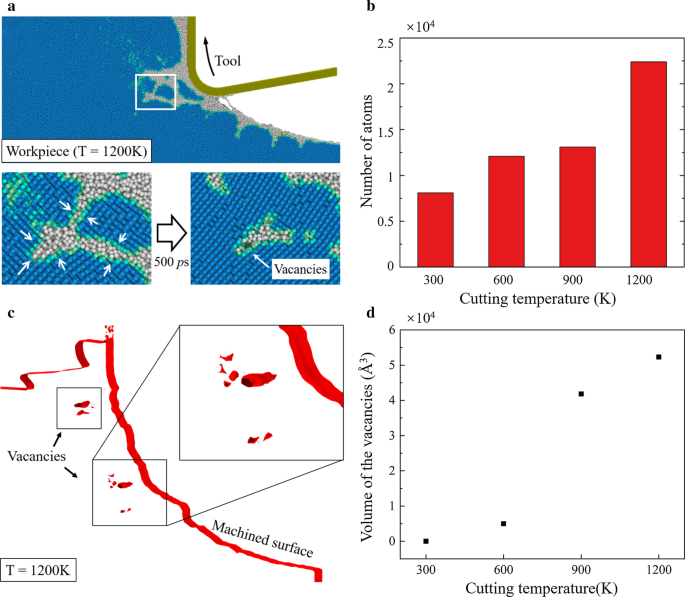
緩和プロセスとワークピースの空孔。 a 1200Kでのワークピースの損傷パターンのスナップショット。 b 非ダイヤモンド構造からSi-I相に変換された原子の数。 c 1200Kでのワークピースの構築された表面メッシュ。 d さまざまな温度での空孔の量

空孔の詳細な分析を図10に示します。空孔の生成を監視するために、機械加工された表面の下の材料要素が選択されます。非ダイヤモンド構造の原子数と材料元素の応力進展が存在します。切削プロセス中、材料要素は最初に圧縮され、次に工具の上方への移動により引張応力を受けると結論付けられます。一方、300 Kでは、切削工具が通過するにつれて損傷領域のせん断応力が増加するため、せん断応力の2つのピークが観察されます。切削温度を上げると、引張応力よりもせん断応力の減少が顕著になります。 1200 Kでは、せん断応力の2番目のピークがほぼなくなり、緩和プロセス中に材料要素の引張応力が支配的になります。

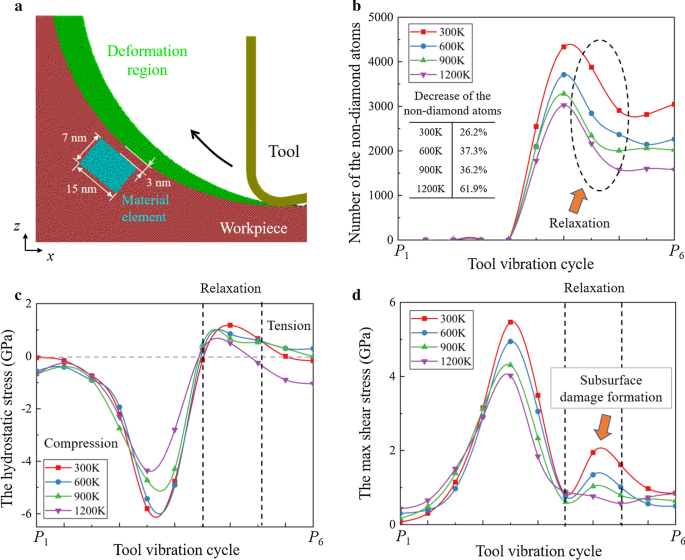
HMプロセス中のリラクゼーション。 a 素材要素のイラスト。 b 材料要素の非ダイヤモンド構造の原子の統計。 c 、 d 材料要素の応力変化

空孔の形成過程に対する引張応力の影響を調査するために、バルクシリコンサンプルの緩和シミュレーションを実施しました。 As shown in Fig. 11a, the initial model composes of 40% Si-I atoms and 60% a-Si atoms, which is generated by the melting-quench method [64]. The size of the model is 21.7 nm × 8.1 nm × 26.1 nm in x 、 y 、および z direction, which contains 230,400 atoms. The initial interface between crystal and non-crystal region is set as (001) crystal plane. Periodic boundary condition is applied in three dimensions to mimic bulk materials. The constructed surface mesh of the relaxed model is present in Fig. 11b. Furthermore, to quantify the vacancies, the solid volume fraction is calculated as the ratio of the solid material volume and the total volume of the simulation sample, as shown in Fig. 11c. It is observed that when temperature is increased, the solid volume fraction decreased obviously under tensile stress. Therefore, to suppress the vacancies, the desired cutting temperature in HM process should be lower than that in ordinary TAC. Meanwhile, the vibration parameters should be optimized to reduce the tensile stress in subsurface workpiece.

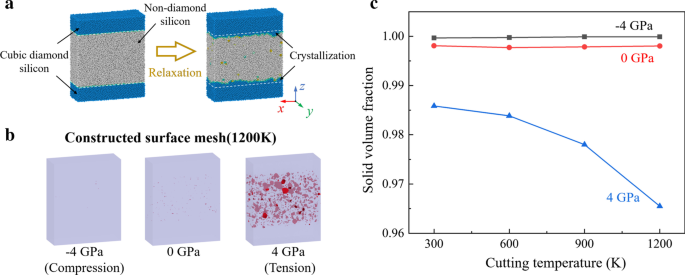
Relaxation simulation of silicon. a Scheme of MD relaxation simulation. b The surface mesh of the relaxed model at 1200 K. c The solid volume fraction curves

結論

In this paper, MD simulation is carried out to investigate the cutting mechanism of hybrid machining (HM) process. A modified cutting model is applied to reveal the material removal behavior and subsurface damage formation in one vibration cycle. The main conclusions were as follows:

1. (1)

   During HM process, the dominant material removal mechanism could transform from extrusion to shear in a single vibration cycle. With an increase of the cutting temperature, the generation and propagation of cracks can be effectively suppressed. However, the swelling appears when the dominant material removal mechanism becomes shearing, which is caused by the rotation of the crystal grains in workpiece.

2. (2)

   Based on the stress analysis, the dominant formation mechanism of the subsurface damage in one vibration cycle can be distinct. In the extrusion stage, the subsurface damage can be generated by the shear stress in the damage region. While in the shearing stage, tensile stress becomes dominant in subsurface damage formation. When the cutting temperature is increased, although the tensile stress concentration in the subsurface workpiece is still obvious, the peak value of the stresses is apparently decreased, which effectively suppress the cracks and fractures in workpiece.

3. (3)

   When the cutting temperature is increased, less subsurface damage is generated in the workpiece. However, due to the tensile stress, some vacancies can be generated in the workpiece when the cutting temperature is increased. Therefore, the desired cutting temperature during HM process should be lower than that in ordinary TAC and the vibration parameters should be set carefully to suppress the vacancies in the subsurface workpiece.

データと資料の可用性

The datasets used and analyzed in the current study can be obtained from the corresponding authors upon reasonable request.

略語

TAC:

Thermal assisted cutting

VAC:

Vibration assisted cutting

LVC:

Linear vibration cutting

EVC:

Elliptical vibration cutting

DOC:

Depth of cut

HM:

Hybrid machining

FEM：

有限要素法

MD：

分子動力学

LAMMPS：

大規模な原子/分子の大規模並列シミュレータ

MEAM:

Modified embedded-atom method

SW:

Stillinger–Weber

COMB:

Charge optimized many-body

ABOP:

Analytical bond-order potential

Si-II:

Metallic stable phase

HPPT:

High-pressure phase transition

CNA:

Common neighbor analysis

a-Si:

Amorphous phase

Si-I:

Single-crystal silicon phase

FCC：

Face Center Cubic

CRSS:

Critical resolved shear stress